湖北省十堰市五校联考2021-2022学年八年级下学期数学第一次月考试卷
试卷更新日期:2022-05-07 类型:月考试卷
一、单选题
-
1. 下列根式是最简二次根式的( )A、 B、 C、 D、2. 下列各式中,计算正确的是( )A、 B、 C、 D、3. 下列命题的逆命题是真命题的有( )
①等边三角形是锐角三角形;②全等三角形的对应角相等;③平行四边形的对角线相互平分;④两组对角分别相等的四边形是平行四边形.
A、③④ B、①②③ C、②③④ D、②③4. 如图在Rt 中, , , ,在 上截取 ,在 上截取 , 在数轴上, 为原点,则 点对应的实数是( )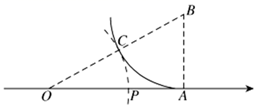 A、 B、 C、 D、5. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为( )
A、 B、 C、 D、5. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为( ) A、9 B、6 C、4 D、36. 下列结论正确的是( )A、 B、若 , 化简 C、 D、若x表示的整数部分,y表示它的小数部分,则7. 甲、乙两艘客轮同时离开港口,航行的速度都是 , 甲客轮15min到达A,乙客轮用20min到达B点,若A、B两点的直线距离为1000m,甲客轮沿北偏东30°的方向航行,则乙客轮的航行方向是( )A、南偏西30° B、南偏东60° C、北偏西30°或南偏东30° D、南偏东60°或北偏西60°8. 如图,EF过对角线的交点O,交AD于点E,交BC于点F.则①;②若 , , 则;③;④图中共有4对全等三角形;⑤.其中正确结论的有( )个.
A、9 B、6 C、4 D、36. 下列结论正确的是( )A、 B、若 , 化简 C、 D、若x表示的整数部分,y表示它的小数部分,则7. 甲、乙两艘客轮同时离开港口,航行的速度都是 , 甲客轮15min到达A,乙客轮用20min到达B点,若A、B两点的直线距离为1000m,甲客轮沿北偏东30°的方向航行,则乙客轮的航行方向是( )A、南偏西30° B、南偏东60° C、北偏西30°或南偏东30° D、南偏东60°或北偏西60°8. 如图,EF过对角线的交点O,交AD于点E,交BC于点F.则①;②若 , , 则;③;④图中共有4对全等三角形;⑤.其中正确结论的有( )个.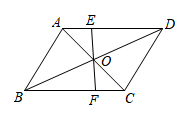 A、2个 B、3个 C、4个 D、5个9. 如图,分别以Rt△ABC的三边为边长向外作等边三角形.若AB=4,则三个等边三角形的面积之和是( )
A、2个 B、3个 C、4个 D、5个9. 如图,分别以Rt△ABC的三边为边长向外作等边三角形.若AB=4,则三个等边三角形的面积之和是( ) A、8 B、6 C、18 D、1210. 如图,的面积为5,它的两条对角线交于点 , 以AB、为两邻边作平行四边形 , 平行四边形的对角线交BD于点 , 同样以AB、为两邻边作平行四边形 , …,依此类推,则平行四边形的面积为( )
A、8 B、6 C、18 D、1210. 如图,的面积为5,它的两条对角线交于点 , 以AB、为两邻边作平行四边形 , 平行四边形的对角线交BD于点 , 同样以AB、为两邻边作平行四边形 , …,依此类推,则平行四边形的面积为( )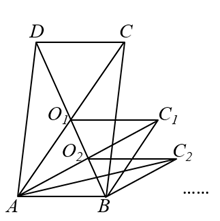 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图, 中, 于点E, 于点F, 与 交于点H,则 度.
 12. 如图,中,对角线AC,BD交于点O, , 若 , , 则BD的长为.
12. 如图,中,对角线AC,BD交于点O, , 若 , , 则BD的长为.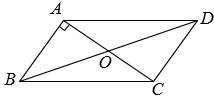 13. 对于任意的正数m,n定义运算为: , 计算的结果为.14. 若等腰三角形的两条边a,b满足 , 则等腰三角形的周长为.15. 如图,在矩形ABCD中, , , 点E,F分别为BC,AD上一点,连接EF,将四边形CDFE沿EF所在直线折叠,使点C恰好与点A重合,点D落在处,则AE的长为.
13. 对于任意的正数m,n定义运算为: , 计算的结果为.14. 若等腰三角形的两条边a,b满足 , 则等腰三角形的周长为.15. 如图,在矩形ABCD中, , , 点E,F分别为BC,AD上一点,连接EF,将四边形CDFE沿EF所在直线折叠,使点C恰好与点A重合,点D落在处,则AE的长为.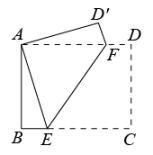 16. 如图,平行四边形ABCD,对角线BD平分∠ABC,BC=6,∠ABC=45°,在对角线BD上有一动点P,边BC上有一动点Q,使PQ+PC最小,则这个最小值为.
16. 如图,平行四边形ABCD,对角线BD平分∠ABC,BC=6,∠ABC=45°,在对角线BD上有一动点P,边BC上有一动点Q,使PQ+PC最小,则这个最小值为.
三、解答题
-
17. 计算:(1)、(2)、18. 先化简,再求值: ,其中 .19.(1)、已知 , , 求代数式的值.(2)、已知 , 求的值.20. 如图,在正方形网格中,每个小正方形的边长都是1,我们把每个小正方形的顶点叫做格点.利用网格作图:
 (1)、请你在网格中画出长为4的线段AB,长为的线段BC,其中线段AB为水平方向,且以AB,BC为邻边作(图形必须在网格内,且顶点都在格点上).(2)、求(1)中对角线的长.21. 已知CD是的边AB上的高,若 , , , 求AB长.22. 《九章算术》卷九中记载:今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽.问索长几何?译文:今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺.牵着绳索(绳索头与地面接触)退行,在距木柱根部8尺处时绳索用尽.问绳索长是多少?23. 已知:如图,在中,E,F是对角线BD上的两点,连接AE,AF,CE,CF,已知____.(填序号).
(1)、请你在网格中画出长为4的线段AB,长为的线段BC,其中线段AB为水平方向,且以AB,BC为邻边作(图形必须在网格内,且顶点都在格点上).(2)、求(1)中对角线的长.21. 已知CD是的边AB上的高,若 , , , 求AB长.22. 《九章算术》卷九中记载:今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽.问索长几何?译文:今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺.牵着绳索(绳索头与地面接触)退行,在距木柱根部8尺处时绳索用尽.问绳索长是多少?23. 已知:如图,在中,E,F是对角线BD上的两点,连接AE,AF,CE,CF,已知____.(填序号).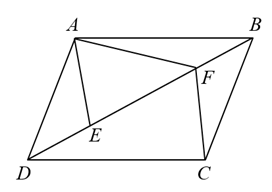 (1)、在① , ②中任选一个作为条件补充在横线上,并完成证明过程.(2)、求证:四边形AECF为平行四边形.24. 在中,.
(1)、在① , ②中任选一个作为条件补充在横线上,并完成证明过程.(2)、求证:四边形AECF为平行四边形.24. 在中,.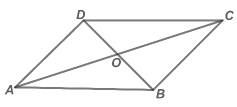 (1)、若 , , 求;(2)、若 , , 求的周长.25. 在学习完《勾股定理》这一章后,小唯和小鹿进行了如下对话:
(1)、若 , , 求;(2)、若 , , 求的周长.25. 在学习完《勾股定理》这一章后,小唯和小鹿进行了如下对话:
根据对话回答问题:
(1)、判断:等边三角形“类勾股三角形”;等腰直角三角形“类勾股三角形”(填“是”或“不是”)(2)、已知其中两边长分别为1, , 若为“类勾股角形”,则另一边长为:.(3)、如果是“类勾股三角形”,它的三边长分别为a,b,c(a,b为直角边且 , c为斜边),用只含有a的式子表示其周长和面积.26. 如图,在平面直角坐标系中,点在y轴正半轴上,点在x轴正半轴上,且..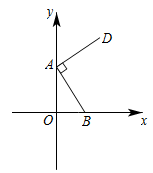 (1)、求AB;(2)、在y轴上是否存在一点P,使得最小?若存在,请求出的最小值;(3)、在x轴上是否存在一点M,使是以AB为腰的等腰三角形?若存在,请直接写出M点坐标.
(1)、求AB;(2)、在y轴上是否存在一点P,使得最小?若存在,请求出的最小值;(3)、在x轴上是否存在一点M,使是以AB为腰的等腰三角形?若存在,请直接写出M点坐标.