湖北省 黄石市2021-2022学年八年级下学期学情检测数学试卷
试卷更新日期:2022-05-07 类型:月考试卷
一、单选题
-
1. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 下列命题的逆命题不正确的是( )A、直角三角形的两锐角互余 B、相等的两个角就一定是对顶角 C、若 , 则 D、全等三角形的三个对应角相等4. 如图,数轴上点A表示的数是0,点B表示的数是1, , 垂足为B,且 , 以A为圆心,长为半径画弧,与数轴交于点D,则点D表示的数为( )
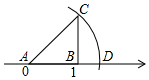 A、1.4 B、 C、 D、25. 已知的三边长为a,4,5(其中)则a的值是( )A、 B、3 C、3或 D、9或416. 一块正方形的瓷砖,面积为50cm2 , 它的边长大约在( )A、4cm~5cm之间 B、5cm~6cm之间 C、6cm~7cm之间 D、7cm~8cm之间7. 若a为正数,则有( )A、a> B、a= C、a< D、a与的关系不确定8. 如图,在△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长为( )
A、1.4 B、 C、 D、25. 已知的三边长为a,4,5(其中)则a的值是( )A、 B、3 C、3或 D、9或416. 一块正方形的瓷砖,面积为50cm2 , 它的边长大约在( )A、4cm~5cm之间 B、5cm~6cm之间 C、6cm~7cm之间 D、7cm~8cm之间7. 若a为正数,则有( )A、a> B、a= C、a< D、a与的关系不确定8. 如图,在△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长为( ) A、2 B、2.6 C、3 D、49. 已知x1= + ,x2= - ,则x₁²+x₂²等于( )A、8 B、9 C、10 D、1110. 如图:已知为直角三角形,分别以直角边、为直径作半圆和 , 以为直径作半圆 , 记两个月牙形阴影部分的面积之和为 , 的面积为 , 则与的大小关系为( )
A、2 B、2.6 C、3 D、49. 已知x1= + ,x2= - ,则x₁²+x₂²等于( )A、8 B、9 C、10 D、1110. 如图:已知为直角三角形,分别以直角边、为直径作半圆和 , 以为直径作半圆 , 记两个月牙形阴影部分的面积之和为 , 的面积为 , 则与的大小关系为( ) A、 B、 C、 D、不能确定
A、 B、 C、 D、不能确定二、填空题
-
11. 计算 的结果是.12. 实数 、 在数轴上位置如图,化简: ;
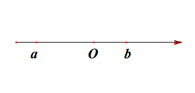 13. 已知长方形的面积是 , 其中一边的长是cm,则该长方形的周长为cm.14. 等式成立的条件是15. 对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形 ,对角线 交于点O.若 ,则 .
13. 已知长方形的面积是 , 其中一边的长是cm,则该长方形的周长为cm.14. 等式成立的条件是15. 对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形 ,对角线 交于点O.若 ,则 .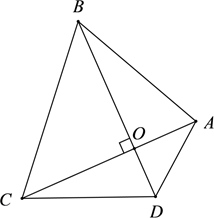 16. 已知中, , , 边上的高 , 则.17. 观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…,请你写出具有以上规律的第⑥组勾股数:18. 如图,两条互相垂直的直线m、n交于点O,一块等腰直角三角尺的直角顶点A在直线m上,锐角顶点B在直线n上,D是斜边BC的中点.已知OD= , BC=4,则S△AOB=.
16. 已知中, , , 边上的高 , 则.17. 观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…,请你写出具有以上规律的第⑥组勾股数:18. 如图,两条互相垂直的直线m、n交于点O,一块等腰直角三角尺的直角顶点A在直线m上,锐角顶点B在直线n上,D是斜边BC的中点.已知OD= , BC=4,则S△AOB=.
三、解答题
-
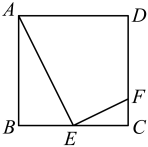
19. 计算:(1)、(2)、20. 先化简再求值: , 其中21. 如图,在正方形中,E是的中点,F是上一点,且.
 (1)、若的长度为1,求的长度和的长度.(2)、求证.22. 如图是单位长度为1的正方形网格.
(1)、若的长度为1,求的长度和的长度.(2)、求证.22. 如图是单位长度为1的正方形网格. (1)、在图1中画出一条长度为的线段AB;(2)、在图2中画出一个以格点为顶点,面积为5的正方形.23. 如图,在中, , 于点M.
(1)、在图1中画出一条长度为的线段AB;(2)、在图2中画出一个以格点为顶点,面积为5的正方形.23. 如图,在中, , 于点M.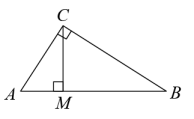 (1)、若 , , 则的长度为多少?(2)、若 , , 则的长度为多少?24. 勾股定理在全世界有超过400种证法,下面介绍欧几里得的证法:(不得直接运用勾股定理结论进行证明)
(1)、若 , , 则的长度为多少?(2)、若 , , 则的长度为多少?24. 勾股定理在全世界有超过400种证法,下面介绍欧几里得的证法:(不得直接运用勾股定理结论进行证明)在中,分别以 , , 为边向外侧做正方形,分别得到正方形 , 正方形 , 正方形.
 (1)、如图1,连接 , , 试证明线段和线段BE的数量关系.(2)、如图2,过点C作直线交正方形中边于点H,边于点l,求证:.(3)、设 , , , 运用此图合勾股定理的学习经验证明结论:.(不得直接运用勾股定理结论证明)25. 已知直线交两坐标轴于 , 两点,且a,b满足 , 点P为直线上第一象限内一动点,过点P作的垂线与过点B平行于x轴的直线相交于点Q.
(1)、如图1,连接 , , 试证明线段和线段BE的数量关系.(2)、如图2,过点C作直线交正方形中边于点H,边于点l,求证:.(3)、设 , , , 运用此图合勾股定理的学习经验证明结论:.(不得直接运用勾股定理结论证明)25. 已知直线交两坐标轴于 , 两点,且a,b满足 , 点P为直线上第一象限内一动点,过点P作的垂线与过点B平行于x轴的直线相交于点Q.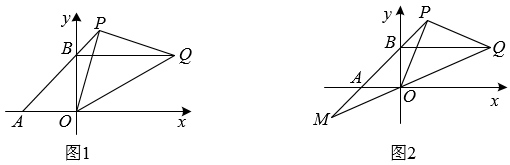 (1)、求A,B两点的坐标.(2)、如图1,当点P在直线上的第一象限内运动时,求的值.(3)、如图2,延长与直线交于点M.试证明: , , 之间的数量关系.
(1)、求A,B两点的坐标.(2)、如图1,当点P在直线上的第一象限内运动时,求的值.(3)、如图2,延长与直线交于点M.试证明: , , 之间的数量关系.