湖北省黄冈市2021-2022学年八年级下学期第一次测评数学试卷

试卷更新日期：2022-05-07 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列各式一定是二次根式的是（）

A、 $\sqrt{- 7}$ B、 $\sqrt[3]{2 m}$ C、 $\sqrt{a^{2} + 1}$ D、 $\sqrt{\frac{a}{b}}$

查看试题解析
2. 在平面直角坐标系中，已知点P的坐标为（5、12），则OP的长为（）

A、5 B、12 C、13 D、14

查看试题解析
3. 如果 $a b > 0$ ， $a + b < 0$ ，那么下面各式：① $\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}$ ， ② $\sqrt{\frac{a}{b}} \times \sqrt{\frac{b}{a}} = 1$ ， ③ $\sqrt{a b} \div \sqrt{\frac{a}{b}} = - b$ ，其中正确的是（）.

A、①② B、②③ C、①③ D、①②③

查看试题解析
4. 在下列长度的四组线段中，不能组成直角三角形的是（）

A、 $a = 5$ ， $b = 12$ ， $c = 13$ B、 $a = b = \sqrt{2}$ ， $c = 2$ C、 $a ： b ： c = 1 ： 2 ： \sqrt{5}$ D、 $a = 4$ ， $b = 5$ ， $c = 6$

查看试题解析
5. 如图，在Rt△ABC中，∠ACB=90∘，以点A为圆心，AC长为半径作圆弧交边AB于点D．若AC=3，BC=4.则BD的长是（）

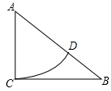A、2 B、3 C、4 D、5

查看试题解析
6. 底面周长为12，高为8的圆柱体上有一只小蚂蚁要从A点爬到B点，则蚂蚁爬行的最短距离是（）

A、10 B、8 C、5 D、4

查看试题解析
7. 在化简 $\frac{x - y}{\sqrt{x} + \sqrt{y}}$ 时，甲、乙两位同学的解答如下：
甲： $\frac{x - y}{\sqrt{x} + \sqrt{y}} = \frac{(x - y) (\sqrt{x} - \sqrt{y})}{(\sqrt{x} + \sqrt{y}) (\sqrt{x} - \sqrt{y})} = \frac{(x - y) (\sqrt{x} - \sqrt{y})}{{(\sqrt{x})}^{2} - {(\sqrt{y})}^{2}} = \sqrt{x} - \sqrt{y}$ ；
乙： $\frac{x - y}{\sqrt{x} + \sqrt{y}} = \frac{{(\sqrt{x})}^{2} - {(\sqrt{y})}^{2}}{\sqrt{x} + \sqrt{y}} = \frac{(\sqrt{x} - \sqrt{y}) (\sqrt{x} + \sqrt{y})}{\sqrt{x} + \sqrt{y}} = \sqrt{x} - \sqrt{y}$ .
这两位同学的解法，你认为（）

A、两人解法都对 B、甲错乙对 C、甲对乙错 D、两人都错

查看试题解析
8. 如图，在平面直角坐标系中，O为坐标原点，四边形OABC是长方形，点A、C的坐标分别为A（10，0 ），C（0，4），点D是OA的中点，点P在BC边上运动，当△ODP是腰长为5的等腰三角形时，点P的坐标为（）

A、（3，4），（2，4） B、（3，4），（2，4），（8，4） C、（2，4），（8，4） D、（3，4），（2，4），（8，4），（2.5，4）

查看试题解析

二、填空题

9. 若x＜3，则 $\sqrt{(x - π)^{2}}$ ＝.

查看试题解析
10. 计算： ${(3 - 2)}^{2020} {(3 + 2)}^{2021} =$ .

查看试题解析
11. 如图，学校有一块长方形花圃，有极少数同学为了避开拐角走“捷径”，在花圃内走出了一条“路”，他们仅仅少走了米，却踩伤了花草．

查看试题解析
12. 已知a、b、c是△ABC三边的长，且满足关系式 $\sqrt{c^{2} - a^{2} - b^{2}} + | a - b | = 0$ ，
则△ABC的形状为

查看试题解析
13. 如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A、B、C、D的面积分别为2，5，1，2．则最大的正方形E的面积是

查看试题解析
14.
如图，在平面直角坐标系中，点A，B的坐标分别为（﹣6，0）、（0，8）．以点A为圆心，以AB长为半径画弧，交x正半轴于点C，则点C的坐标为

查看试题解析
15. 明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》：“平地秋千未起，踏板一尺离地，送行二步恰竿齐，五尺板高离地…”翻译成现代文为：如图，秋千OA静止的时候，踏板离地高一尺（ $A C = 1$ 尺），将它往前推进两步（ $E B = 10$ 尺），此时踏板升高离地五尺（ $B D = 5$ 尺），则秋千绳索（OA或OB）的长度为尺.

查看试题解析
16. 如图，四个全等的直角三角形按如图所示的方式围成正方形ABCD，过各较长直角边的中点作垂线，围成面积为S的小正方形EFGH.已知AM为 $R t △ A B M$ 较长直角边， $A M = 2 \sqrt{3} E F$ ，则正方形ABCD的面积为S.

查看试题解析

三、解答题

17. 计算：

(1)、 $(\sqrt{12} - \sqrt{\frac{2}{3}}) \div \sqrt{3}$ ；

(2)、 $\sqrt{27} - (5 \sqrt{\frac{1}{3}} + \sqrt{75})$ .

查看试题解析
18. 已知x=2+ $\sqrt{3}$ ，y=2- $\sqrt{3}$ ．试求代数式 $\frac{x}{y} + \frac{y}{x}$ 的值．

查看试题解析
19. 如图，两艘海舰在海上进行为时2小时的军事演习，一海舰以120海里/时的速度从港口A出发，向北偏东60°方向航行到达B，另一海舰以90海里/时的速度同时从港口A出发，向南偏东30°方向航行到达C，则此时两艘海舰相距多少海里？

查看试题解析
20. 阅读下面的解答过程，然后作答：
有这样一类题目：将 $\sqrt{a + 2 \sqrt{b}}$ 化简，若你能找到两个数 m和n，使m²+n²=a 且 mn= $\sqrt{b}$ ，则a+2 $\sqrt{b}$ 可变为m²+n²+2mn，即变成（m+n）² ，从而使得 $\sqrt{a + 2 \sqrt{b}}$ 化简.

例如：∵5+2 $\sqrt{6}$ =3+2+2 $\sqrt{6}$ =（ $\sqrt{3}$ ）²+（ $\sqrt{2}$ ）²+2 $\sqrt{6}$ =（ $\sqrt{3}$ + $\sqrt{2}$ ）²

∴ $\sqrt{5 + 2 \sqrt{6}}$ = $\sqrt{{(\sqrt{3} + \sqrt{2})}^{2}}$ = $\sqrt{3}$ + $\sqrt{2}$

请你仿照上例将下列各式化简

(1)、 $\sqrt{4 + 2 \sqrt{3}}$

(2)、 $\sqrt{7 - 2 \sqrt{10}}$ .

查看试题解析
21. 如图，某中学有一块四边形的空地ABCD，学校计划在空地上种植草皮，经测量 $∠ B = 90 °$ ， $A B = 3$ 米， $B C = 4$ 米， $C D = 12$ 米， $A D = 13$ 米，若每平方米草皮需要200元，问学校需要投入多少资金买草皮？

查看试题解析
22. 如图，有一张边长为 $6 \sqrt{3} c m$ 的正方形纸板，现将该纸板的四个角剪掉，制作一个有底无盖的长方体盒子，剪掉的四个角是面积相等的小正方形，此小正方形的边长为3 $c m$ .求：

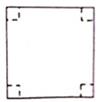(1)、剪掉四个角后，制作长方体盒子的纸板的面积；

(2)、长方体盒子的体积.

查看试题解析
23. 如图，Rt△ABC中，∠C=90°，AD平分∠CAB，DE⊥AB于E，若AC=6，BC=8，CD=3．

(1)、求DE的长；

(2)、求△ADB的面积．

查看试题解析
24. 如图，C为线段BD上一动点，分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC，已知AB＝5，DE＝1，BD＝8，设CD＝x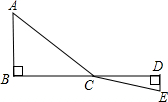

(1)、用含x的代数式表示AC+CE的长；

(2)、请问点C满足什么条件时，AC+CE的值最小？

(3)、根据（2）中的规律和结论，请构图求出代数式 $\sqrt{x^{2} + 4} + \sqrt{(12 - x)^{2} + 9}$ 的最小值.

查看试题解析
25. 如图（1），在平面直角坐标系中点 $A (x ， y)$ ， $B (2 x ， 0)$ 满足 $| x - \sqrt{3} | + \sqrt{y - x} = 0$ ，点C为线段OB上一个动点，以CA为腰作等腰直角 $△ A C D$ ，且 $A C = A D$ .

(1)、求点A、B的坐标及 $△ A O B$ 的面积；

(2)、试判断CD、OC、BC间的数量关系，并说明理由；

(3)、如图（2），若点C为线段OB延长线上一个动点，则（2）中的结论是否成立，并说明理由.

查看试题解析