河南省驻马店市部分校2021-2022学年八年级下学期第一次学情反馈数学试卷

试卷更新日期：2022-05-07 类型：月考试卷

进入出卷网下载

一、单选题

1. 在数轴上表示不等式 $x > 1$ 的解集，正确的是（）.

A、 B、 C、 D、

查看试题解析
2. 已知△ABC的三个内角分别为∠A、∠B、∠C，三边分别为a、b、c，下列条件不能判定△ABC是直角三角形的是（）

A、∠A：∠B：∠C＝3：4：7 B、∠A＝∠B﹣∠C C、a：b：c＝2：3：4 D、b²＝（a+c）（a﹣c）

查看试题解析
3.
若图示的两架天平都保持平衡，则对a、b、c三种物体的重量判断正确的是（　　）

A、a＞c B、a＜c C、a＜b D、b＜c

查看试题解析
4. 如图，OP平分∠AOB，E为OA上一点，OE＝4，P到OB的距离是2，则△OPE的面积为（）

A、2 B、3 C、4 D、8

查看试题解析
5. 下列说法中错误的是（）

A、若 $a < b$ ，则 $a + 1 < b + 1$ B、若 $- 2 a > - 2 b$ ，则 $a < b$ C、若 $a < b$ ，则 $a c < b c$ D、若 $a (c^{2} + 1) < b (c^{2} + 1)$ ，则 $a < b$

查看试题解析
6. 已知方程组 ${\begin{array}{l} 2 x + y = 1 - m \\ x + 2 y = 2 \end{array}$ 的x，y满足x﹣y≥0，则m的取值范围是（）

A、m≤﹣1 B、m≥﹣1 C、m≤1 D、m≥1

查看试题解析
7. “三等分角”大约是在公元前五世纪由古希腊人提出来的。借助如图所示的“三等分角仪”能三等分任一角。这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动，C点固定，OC=CD=DE，点D，E可在槽中滑动，若∠BDE=75°，则∠CDE的度数是（）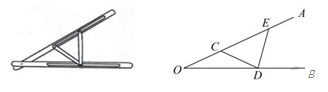

A、60° B、65° C、75° D、80°

查看试题解析
8. 如图，直线l₁、l₂、l₃表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则供选择的地址有（）

A、1处 B、2处 C、3处 D、4处

查看试题解析
9. 已知a，b为常数，若ax＋b＞0的解是x< $\frac{1}{3}$ ，则bx－a<0的解是（）

A、x＞－3 B、x <－3 C、x ＞ 3 D、x < 3

查看试题解析
10. 如图，点I是△ABC三条角平分线的交点，△ABI的面积记为S₁ ， △ACI的面积记为S₂ ， △BCI的面积记为S₃ ，关于S₁+S₂与S₃的大小关系，正确的是（）

A、S₁+S₂＝S₃ B、S₁+S₂＜S₃ C、S₁+S₂＞S₃ D、无法确定

查看试题解析

二、填空题

11. 某产品进价为每件200元，商店标价为每件300元.现商店准备将这批服装打折出售，但要保证毛利润不低于5%，则商店最低可按折出售.

查看试题解析
12. 等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为．

查看试题解析
13. 如图，在△ABC中，AB＝AC，AD＝AE.若∠B＝55°，∠BAD＝50°，则∠EDC＝°.

查看试题解析
14. 2022年北京冬奥会已经越来越近了，这是我国重要历史节点的重大标志性活动，更是全国人民的一次冰雪运动盛宴，与此同时北京冬奥会吉祥物冰墩墩也受到人们的喜爱，关于冰墩墩的各种周边纪念品：徽章、风铃、抱枕、公仔正在某商场火热销售中.已知徽章和抱枕的价格相同，公仔的单价是风铃的两倍，且徽章和风铃的单价之和不超过120元.元旦节期间，徽章的销售数量是公仔数量的2倍，风铃和抱枕的销售数量相同，其中徽章和风铃共卖出120件，抱枕和公仔的销售总额比风铃和徵章的销售总额多2200元，则徽章和风铃销售总额的最大值是元.

查看试题解析
15. 在 $△ A B C$ 中， $A B = A C = 5$ ， $B C = 6$ .若点 P在边AC上移动，则线段BP的最小值是 .

查看试题解析

三、解答题

16. 解下列一元一次不等式，并把它们的解集表示在数轴上：

(1)、2﹣5x＜8﹣6x；

(2)、 $\frac{x - 5}{3}$ +1≤ $\frac{3}{2}$ x.

查看试题解析
17. 如图，C是∠AOB内部一点，D是∠AOB外部一点，在内部求作一点P，使PC＝PD，并且使P点到∠AOB两边距离相等（保留作图痕迹）.

查看试题解析
18. 如图，在直角三角形ABC中，∠ACB＝90°，∠B＝60°，AD ， CE是角平分线，AD与CE相交于点F ， FM⊥AB ， FN⊥BC ，垂足分别为M ， N.求证：FE＝FD．

查看试题解析
19. 如图，在△ABC中，∠ACB=90°，∠A=30°，AB的垂直平分线分别交AB和AC于点D，E.

(1)、求证：AE=2CE；

(2)、连接CD，请判断△BCD的形状，并说明理由.

查看试题解析
20. 如图，在△ABC中，AC=BC，∠C＝90°，AD是△ABC的角平分线，DE⊥AB，垂足为E.

(1)、已知CD=2cm，求AC的长；

(2)、求证：AB=AC+CD.

查看试题解析
21. 如图，在△ABC中，AB＝AC，D为CA延长线上一点，DE⊥BC于点E，交AB于点F.

(1)、求证：△ADF是等腰三角形.

(2)、若AF＝BF＝ $\sqrt{13}$ ，BE＝2，求线段DE的长.

查看试题解析
22. 截至12月25日，全国累计报告接种新型冠状病毒疫苗超过12亿剂次.为了满足市场需求，某公司计划投入10个大、小两种车间共同生产同一种新型冠状病毒疫苗，已知1个大车间和2个小车间每周能生产疫苗共35万剂，2个大车间和1个小车间每周能生产疫苗共40万剂，每个大车间生产1万剂疫苗的平均成本为90万元，每个小车间生产1万剂疫苗的平均成本为80万元.

(1)、该公司每个大车间、小车间每周分别能生产疫苗多少万剂？

(2)、若投入的10个车间每周生产的疫苗不少于135万剂，请问一共有几种投入方案，并求出每周生产疫苗的总成本最小值？

查看试题解析
23. 已知△ABC是等边三角形，D，E分别是直线AC，BC上一点.

(1)、如图，若D在线段AC上，E在BC的延长线上，且DE＝DB.
①当D是线段AC的中点时（如图1），求证：CE＝AD；
②当D不是线段AC的中点时（如图2），过点D作DF∥AB交BC于点F，试确定线段CE与AD的大小关系，并证明你的结论.

(2)、若D是线段AC的延长线上一点，且CD＝CA，当△DBE是等腰三角形时，求∠DEB的度数.

查看试题解析