江苏省扬州市2022年初中毕业、升学统一考试数学模拟试题(一)
试卷更新日期:2022-05-07 类型:中考模拟
一、单选题
-
1. ﹣2018的绝对值的相反数是( )A、 B、﹣ C、2018 D、﹣20182. 下列运算正确的是( )A、x2+x2=x4 B、a2•a3=a5 C、(3x)2 =6x2 D、(mn)5÷(mn)=mn43. A,B是数轴上两点,线段AB上的点表示的数中,有互为相反数的是( )A、
 B、
B、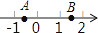 C、
C、 D、
D、 4. 通过估算,估计 的大小应在( )A、7~8之间 B、8.0~8.5之间 C、8.5~9.0之间 D、9~10之间5.
4. 通过估算,估计 的大小应在( )A、7~8之间 B、8.0~8.5之间 C、8.5~9.0之间 D、9~10之间5.已知:如图,OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,则∠ACB的度数为( )
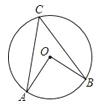 A、45° B、35° C、25° D、20°6. 为庆祝首个“中国农民丰收节”,十渡镇西河村举办“西河稻作文化节”活动.西河水稻种植历史悠久,因“色白粒粗,味极香美,七煮不烂”而享誉京城.已知每粒稻谷重约0.000035千克,将0.000035用科学记数法表示应为( )A、35×10﹣6 B、3.5×10﹣6 C、3.5×10﹣5 D、0.35×10﹣47. 如图,点A,B,P是⊙O上的三点,若 ,则∠APB的度数为( )
A、45° B、35° C、25° D、20°6. 为庆祝首个“中国农民丰收节”,十渡镇西河村举办“西河稻作文化节”活动.西河水稻种植历史悠久,因“色白粒粗,味极香美,七煮不烂”而享誉京城.已知每粒稻谷重约0.000035千克,将0.000035用科学记数法表示应为( )A、35×10﹣6 B、3.5×10﹣6 C、3.5×10﹣5 D、0.35×10﹣47. 如图,点A,B,P是⊙O上的三点,若 ,则∠APB的度数为( ) A、80° B、140° C、20° D、50°8. 将抛物线y= x2﹣6x+21向左平移2个单位后,得到新抛物线的解析式为( )A、y= (x﹣8)2+5 B、y= (x﹣4)2+5 C、y= (x﹣8)2+3 D、y= (x﹣4)2+3
A、80° B、140° C、20° D、50°8. 将抛物线y= x2﹣6x+21向左平移2个单位后,得到新抛物线的解析式为( )A、y= (x﹣8)2+5 B、y= (x﹣4)2+5 C、y= (x﹣8)2+3 D、y= (x﹣4)2+3二、填空题
-
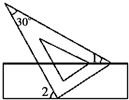
9. 若am=2,an=3,则am﹣n的值为.10. 因式分解: =.11. 如图,将一块含有30°角的直角三角板的两个顶点叠放在长方形的两条对边上,如果∠1=27°,那么∠2=°
 12. 已知关于 的方程 有两个相等的实数根,那么 的值为.13. 已知:M,N两点关于y轴对称,点M的坐标为(a,b),且点M在双曲线y= 上,点N在直线y=x+3上,则抛物线y=﹣abx2+(a+b)x的顶点坐标是.14. 某次数学测试,某班一个学习小组的六位同学的成绩如下:84、75、75、92、86、99,则这六位同学成绩的中位数是.15. 如图,在△ABC中,DE∥BC,若AD=1,DB=2,则的值为.
12. 已知关于 的方程 有两个相等的实数根,那么 的值为.13. 已知:M,N两点关于y轴对称,点M的坐标为(a,b),且点M在双曲线y= 上,点N在直线y=x+3上,则抛物线y=﹣abx2+(a+b)x的顶点坐标是.14. 某次数学测试,某班一个学习小组的六位同学的成绩如下:84、75、75、92、86、99,则这六位同学成绩的中位数是.15. 如图,在△ABC中,DE∥BC,若AD=1,DB=2,则的值为. 16. 如图,⊙O的半径为 ,圆心与坐标原点重合,在直角坐标系中,把横坐标、纵坐标都是整数的点称为格点,则⊙O上格点有个,设L为经过⊙O上任意两个格点的直线,则直线L同时经过第一、二、四象限的概率是.
16. 如图,⊙O的半径为 ,圆心与坐标原点重合,在直角坐标系中,把横坐标、纵坐标都是整数的点称为格点,则⊙O上格点有个,设L为经过⊙O上任意两个格点的直线,则直线L同时经过第一、二、四象限的概率是.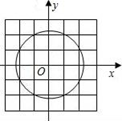 17. 如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为 .
17. 如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为 .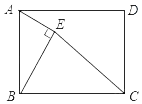 18. 如图,已知长方体的三条棱AB、BC、BD分别为4,5,2,蚂蚁从A点出发沿长方体的表面爬行到M的最短路程的平方是.
18. 如图,已知长方体的三条棱AB、BC、BD分别为4,5,2,蚂蚁从A点出发沿长方体的表面爬行到M的最短路程的平方是. 19. “2015扬州鉴真国际半程马拉松”的赛事共有三项:A、“半程马拉松”、B、“10公里”、C、“迷你马拉松”.小明和小刚参加了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组(1)、小明被分配到“迷你马拉松”项目组的概率为(2)、求小明和小刚被分配到不同项目组的概率.
19. “2015扬州鉴真国际半程马拉松”的赛事共有三项:A、“半程马拉松”、B、“10公里”、C、“迷你马拉松”.小明和小刚参加了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组(1)、小明被分配到“迷你马拉松”项目组的概率为(2)、求小明和小刚被分配到不同项目组的概率.三、解答题
-
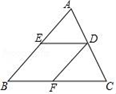
20.(1)、计算:(2)、化简:.21.(1)、解方程2(x﹣3)=4x﹣5(2)、解不等式组:22. 如图,在△ABC中,点D是AC的中点,DE∥BC交AB于点E,DF∥AB交BC于点F,说明△ADE与△DCF全等的理由.
 23. 在△ABC中,∠C=90°.(1)、已知c=8 , ∠A=60°,求∠B,a,b;(2)、已知a=3 , ∠A=45°,求∠B,b,c.24. 如图,在平面直角坐标系xOy中,点A(a,﹣ )在直线y=﹣ 上,AB∥y轴,且点B的纵坐标为1,双曲线y= 经过点B.
23. 在△ABC中,∠C=90°.(1)、已知c=8 , ∠A=60°,求∠B,a,b;(2)、已知a=3 , ∠A=45°,求∠B,b,c.24. 如图,在平面直角坐标系xOy中,点A(a,﹣ )在直线y=﹣ 上,AB∥y轴,且点B的纵坐标为1,双曲线y= 经过点B. (1)、求a的值及双曲线y= 的解析式;(2)、经过点B的直线与双曲线y= 的另一个交点为点C,且△ABC的面积为 .
(1)、求a的值及双曲线y= 的解析式;(2)、经过点B的直线与双曲线y= 的另一个交点为点C,且△ABC的面积为 .①求直线BC的解析式;
②过点B作BD∥x轴交直线y=﹣ 于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
25. 如图,AB为⊙O的直径,点C,D在⊙O 上,且点C是弧BD的中点,过点C作AD的垂线EF交直线AD于点E. (1)、求证:EF 是⊙O 的切线;(2)、连接 BC,若 AB=5,BC=3,求线段 AE 的长.26. 已知抛物线y=x2+bx+c经过点(1,0)和点(0,3).(1)、求此抛物线的解析式及顶点坐标;(2)、当自变量x满足﹣1≤x≤3时,求函数值y的取值范围;(3)、将此抛物线沿x轴平移m个单位后,当自变量x满足1≤x≤5时,y的最小值为5,求m的值.27. 某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如表:
(1)、求证:EF 是⊙O 的切线;(2)、连接 BC,若 AB=5,BC=3,求线段 AE 的长.26. 已知抛物线y=x2+bx+c经过点(1,0)和点(0,3).(1)、求此抛物线的解析式及顶点坐标;(2)、当自变量x满足﹣1≤x≤3时,求函数值y的取值范围;(3)、将此抛物线沿x轴平移m个单位后,当自变量x满足1≤x≤5时,y的最小值为5,求m的值.27. 某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如表:x/元
…
15
20
25
…
y/件
…
25
20
15
…
已知日销售量y是销售价x的一次函数.
(1)、求日销售量y(件)与每件产品的销售价x(元)之间的函数表达式;(2)、当每件产品的销售价定为35元时,此时每日的销售利润是多少元?28. 问题发现.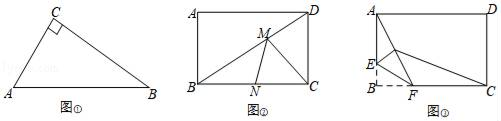 (1)、如图①,Rt△ABC中,∠C=90°,AC=3,BC=4,点D是AB边上任意一点,则CD的最小值为 .(2)、如图②,矩形ABCD中,AB=3,BC=4,点M、点N分别在BD、BC上,求CM+MN的最小值.(3)、如图③,矩形ABCD中,AB=3,BC=4,点E是AB边上一点,且AE=2,点F是BC边上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG、CG,四边形AGCD的面积是否存在最小值,若存在,求这个最小值及此时BF的长度.若不存在,请说明理由.
(1)、如图①,Rt△ABC中,∠C=90°,AC=3,BC=4,点D是AB边上任意一点,则CD的最小值为 .(2)、如图②,矩形ABCD中,AB=3,BC=4,点M、点N分别在BD、BC上,求CM+MN的最小值.(3)、如图③,矩形ABCD中,AB=3,BC=4,点E是AB边上一点,且AE=2,点F是BC边上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG、CG,四边形AGCD的面积是否存在最小值,若存在,求这个最小值及此时BF的长度.若不存在,请说明理由.