江苏省盐城市建湖县2022年中考一模数学试卷
试卷更新日期:2022-05-07 类型:中考模拟
一、单选题
-
1. 温度由﹣3℃上升8℃是( )A、5℃ B、﹣5℃ C、11℃ D、﹣11℃2. 下列计算结果正确的是( ).A、 B、 C、 D、3. 由4个大小相同的小正方体搭成的如图所示的几何体,则这个几何体的俯视图是( ).
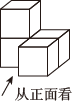 A、
A、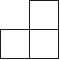 B、
B、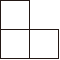 C、
C、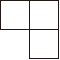 D、
D、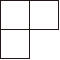 4. 如图, , 将一副直角三角板作如下摆放,图中点A、B、C在同一直线上,则的度数为( ).
4. 如图, , 将一副直角三角板作如下摆放,图中点A、B、C在同一直线上,则的度数为( ).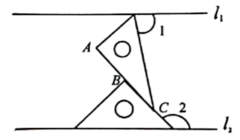 A、60° B、75° C、80° D、85°5. 2、6、m是某三角形三边的长,则等于( ).A、 B、 C、12 D、6. 若一个多边形的内角和是540°,则该多边形的边数为( )A、4 B、5 C、6 D、77. 如图,每个小方格的边长为1,A , B两点都在小方格的顶点上,点C也是图中小方格的顶点,并且△ABC是等腰三角形,那么点C的个数为( )
A、60° B、75° C、80° D、85°5. 2、6、m是某三角形三边的长,则等于( ).A、 B、 C、12 D、6. 若一个多边形的内角和是540°,则该多边形的边数为( )A、4 B、5 C、6 D、77. 如图,每个小方格的边长为1,A , B两点都在小方格的顶点上,点C也是图中小方格的顶点,并且△ABC是等腰三角形,那么点C的个数为( )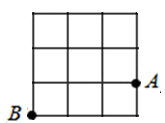 A、1 B、2 C、3 D、48. 如图,游乐园里的原子滑车是很多人喜欢的项目,惊险刺激,原子滑车在轨道上运行的过程中有一段路线可以看作是抛物线的一部分,原子滑车运行的竖直高度 (单位: )与水平距离 (单位: )近似满足函数关系 .下图记录了原子滑车在该路段运行的 与 的三组数据 、 、 ,根据上述函数模型和数据,可推断出,此原子滑车运行到最低点时,所对应的水平距离 满足( )
A、1 B、2 C、3 D、48. 如图,游乐园里的原子滑车是很多人喜欢的项目,惊险刺激,原子滑车在轨道上运行的过程中有一段路线可以看作是抛物线的一部分,原子滑车运行的竖直高度 (单位: )与水平距离 (单位: )近似满足函数关系 .下图记录了原子滑车在该路段运行的 与 的三组数据 、 、 ,根据上述函数模型和数据,可推断出,此原子滑车运行到最低点时,所对应的水平距离 满足( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
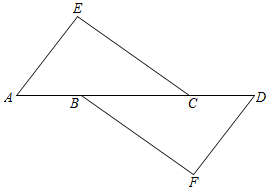
9. 已知一组数据:7、a、6、4、5、7的众数为7,则这组数据的平均数是.10. 把多项式 分解因式,结果为.11. 《2022年政府工作报告》中指出:我国有2.9亿在校学生,要坚持把教育这个关乎千家万户和中华民族未来的大事办好.将2.9亿用科学记数法表示应为.12. 已知方程组 , 则的值为.13. 如图,AE//DF,.添加下列条件中的一个:①;②;③;④EC//BF.其中能证明≌的是 (只填序号).
 14. 如图,在中, , BC的垂直平分线分别交AB、BC于点D、E,若 , , 则的周长为cm.
14. 如图,在中, , BC的垂直平分线分别交AB、BC于点D、E,若 , , 则的周长为cm. 15. 如图,在的内接四边形ABCD中, , , 点E在弧AD上,则的度数为.
15. 如图,在的内接四边形ABCD中, , , 点E在弧AD上,则的度数为.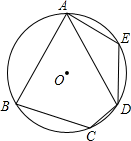 16. 如图,在平面直角坐标系中,O为坐标原点,平行四边形ABCD的边AB在x轴上、顶点D在y轴的正半轴上,点C在第二象限,将沿y轴翻折,使点A落在x轴上的点E处、点B恰好为OE的中点.DE与BC交于点F.若图象经过点C,且 , 则k的值为.
16. 如图,在平面直角坐标系中,O为坐标原点,平行四边形ABCD的边AB在x轴上、顶点D在y轴的正半轴上,点C在第二象限,将沿y轴翻折,使点A落在x轴上的点E处、点B恰好为OE的中点.DE与BC交于点F.若图象经过点C,且 , 则k的值为.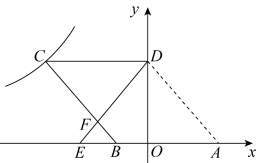
三、解答题
-
17. 计算:.18. 解不等式组 , 并写出该不等式组的最大整数解.19. 先化简,再求值: , 其中.20. 如图,点D、E分别为的边AC、BC的中点,连接DE.求证:
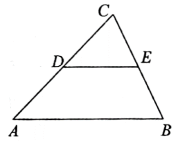 (1)、DE//AB;(2)、.21. 如图,小明和小春制作了两个质地均匀、可以自由转动的转盘,A盘被等分为四个扇形,上面分别标有数字1,2,4,5;B盘中圆心角为120°的扇形上面标有数字3,其余部分上面标有数字4.
(1)、DE//AB;(2)、.21. 如图,小明和小春制作了两个质地均匀、可以自由转动的转盘,A盘被等分为四个扇形,上面分别标有数字1,2,4,5;B盘中圆心角为120°的扇形上面标有数字3,其余部分上面标有数字4.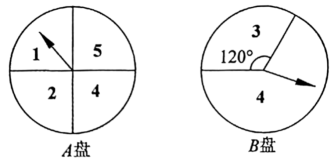 (1)、小明转动一次A盘,指针指向数字为2的概率是;(2)、小明和小春用如图所示的两个转盘做游戏,游戏规则如下:分别旋转两个转盘,将A盘转出的数字作为被减数,B盘转出的数字作为减数;如果差为负数则小春胜;若差为正数,则小明胜.这个游戏对双方公平吗?请用列表或画树状图的方法说明你的理由.22. 3月12日,某初级中学组织学生开展了义务植树社会实践活动.为了了解全校500名学生义务植树情况,小文同学开展了一次调查研究.小文从每个班级随机抽取了5名学生进行调查,并将收集的数据(单位:棵)进行整理、描述,绘制成如下两幅不完整的统计图,根据图中提供的信息解答下列问题:
(1)、小明转动一次A盘,指针指向数字为2的概率是;(2)、小明和小春用如图所示的两个转盘做游戏,游戏规则如下:分别旋转两个转盘,将A盘转出的数字作为被减数,B盘转出的数字作为减数;如果差为负数则小春胜;若差为正数,则小明胜.这个游戏对双方公平吗?请用列表或画树状图的方法说明你的理由.22. 3月12日,某初级中学组织学生开展了义务植树社会实践活动.为了了解全校500名学生义务植树情况,小文同学开展了一次调查研究.小文从每个班级随机抽取了5名学生进行调查,并将收集的数据(单位:棵)进行整理、描述,绘制成如下两幅不完整的统计图,根据图中提供的信息解答下列问题: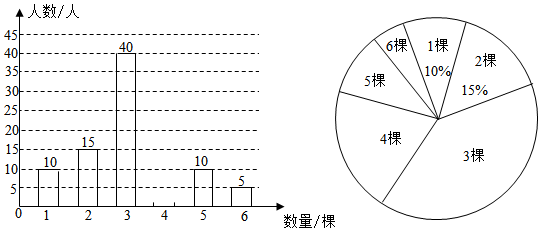 (1)、小文一共随机抽取名学生进行调查;在扇形统计图中,“4棵”所在的扇形的圆心角等于度;(2)、补全条形统计图;(3)、随机抽取的这部分学生义务植树数量的中位数是;(4)、在这次社会实践活动中,学校授予义务植树数量不少于4棵的学生为“植树小能手”的称号,根据调查结果,估计该学校获得“植树小能手”称号的学生有名.23. 如图,等腰中, , , 以C为旋转中心,顺时针旋转到位置,使点A落在BC边的延长线上的E处,连接AD和BD.
(1)、小文一共随机抽取名学生进行调查;在扇形统计图中,“4棵”所在的扇形的圆心角等于度;(2)、补全条形统计图;(3)、随机抽取的这部分学生义务植树数量的中位数是;(4)、在这次社会实践活动中,学校授予义务植树数量不少于4棵的学生为“植树小能手”的称号,根据调查结果,估计该学校获得“植树小能手”称号的学生有名.23. 如图,等腰中, , , 以C为旋转中心,顺时针旋转到位置,使点A落在BC边的延长线上的E处,连接AD和BD.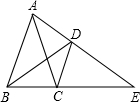 (1)、求证:≌;(2)、请判断的形状,并证明你的结论.24. 3月初某商品价格下跌,每件价格下跌20%,用3000元买到的该商品件数比下跌前多25件.3月下旬该商品开始涨价,经过两次涨价后,该商品价格为每件29.04元.(1)、求3月初该商品下跌后的价格;(2)、若该商品两次涨价率相同,求该商品价格的平均涨价率.25. 如图,在中, , 以BC为直径作 , 交AC于点F,作交AB延长线于点D,E为CD上一点,且.
(1)、求证:≌;(2)、请判断的形状,并证明你的结论.24. 3月初某商品价格下跌,每件价格下跌20%,用3000元买到的该商品件数比下跌前多25件.3月下旬该商品开始涨价,经过两次涨价后,该商品价格为每件29.04元.(1)、求3月初该商品下跌后的价格;(2)、若该商品两次涨价率相同,求该商品价格的平均涨价率.25. 如图,在中, , 以BC为直径作 , 交AC于点F,作交AB延长线于点D,E为CD上一点,且.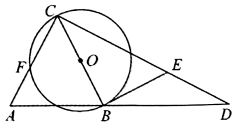 (1)、证明:BE为的切线;(2)、若 , , 求AC与DE的长.26.
(1)、证明:BE为的切线;(2)、若 , , 求AC与DE的长.26.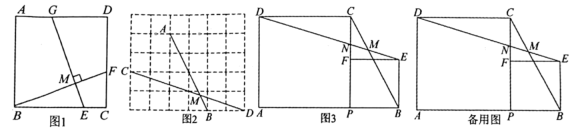 (1)、【问题再现】苏科版《数学》八年级下册第94页有这样一题:
(1)、【问题再现】苏科版《数学》八年级下册第94页有这样一题:如图1,在正方形ABCD中,E,F,G分别是BC,CD,AD上的点, , 垂足为M,那么GEBF(填“<”、“=”或“>”).
(2)、
【迁移尝试】如图2,在5×6的正方形网格中,点A,B,C,D为格点,AB交CD于点M.求的度数;(3)、【拓展应用】如图3,点P是线段AB上的动点,分别以AP,BP为边在AB的同侧作正方形APCD与正方形PBEF,连接DE分别交线段BC,PC于点M,N.
①求的度数;
②连接AC交DE于点H,直接写出的值为______.27. 在平面直角坐标系中,二次函数的图象过点和点 , 与x轴交于点A、B(点A在点B的左边),且点D与点G关于坐标原点对称.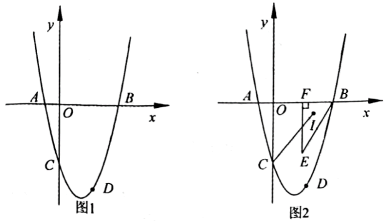 (1)、求该二次函数解析式,并判断点G是否在此函数的图象上,并说明理由;(2)、若点P为此抛物线上一点,它关于x轴,y轴的对称点分别为M,N,问是否存在这样的P点使得M,N恰好都在直线DG上?如存在,求出点P的坐标,如不存在,并说明理由;(3)、若第四象限有一动点E,满足 , 过E作轴于点F,设F坐标为 , , 的内心为I,连接CI,直接写出CI的最小值.
(1)、求该二次函数解析式,并判断点G是否在此函数的图象上,并说明理由;(2)、若点P为此抛物线上一点,它关于x轴,y轴的对称点分别为M,N,问是否存在这样的P点使得M,N恰好都在直线DG上?如存在,求出点P的坐标,如不存在,并说明理由;(3)、若第四象限有一动点E,满足 , 过E作轴于点F,设F坐标为 , , 的内心为I,连接CI,直接写出CI的最小值.