江苏省宿迁市泗阳县2022年中考一模数学试卷

试卷更新日期：2022-05-07 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列函数中是二次函数的是（　　）

A、y＝﹣2x B、y＝﹣ $\frac{6}{x}$ C、y＝1﹣3x² D、y＝x+3

查看试题解析
2. 已知∠A为锐角，且sinA＝ $\frac{1}{2}$ ，那么∠A等于（　　）

A、15° B、30° C、45° D、60°

查看试题解析
3. 方程 $x^{2} - 4 = 0$ 的解是（）

A、 $x_{1} = 2 ， x_{2} = - 2$ B、 $x = 0$ C、 $x_{1} = x_{2} = 2$ D、 $x_{1} = x_{2} = - 2$

查看试题解析
4.
如图，ABCD为⊙O内接四边形，若∠D=85°，则∠B=（　　）

A、85° B、95° C、105° D、115°

查看试题解析
5. 一个箱子里装有8个球，其中5个红球，3个白球，每个球除颜色外其它完全相同，从中任意摸出一个球，是白球的概率是（）

A、 $\frac{1}{8}$ B、 $\frac{5}{8}$ C、 $\frac{3}{5}$ D、 $\frac{3}{8}$

查看试题解析
6. 若a、b、c的平均数为7，则a+1、b+2、c+3的平均数为（　　）

A、7 B、8 C、9 D、10

查看试题解析
7. 下列成语或词语所反映的事件中，可能性大小最小的是（）

A、瓜熟蒂落 B、守株待兔 C、旭日东升 D、夕阳西下

查看试题解析
8. 两个相似三角形，其周长之比为3：2，则其面积比为（）

A、 $\sqrt{3} ： \sqrt{2}$ B、3：2 C、9：4 D、不能确定

查看试题解析
9. 某商场降价销售一批名牌衬衫，已知所获利润y(元)与降价x(元)之间的关系是y=-2x²+60x+800，则利润获得最多为（）

A、15元 B、400元 C、800元 D、1250元

查看试题解析
10. 如图，在 $△ A B C$ 中， $C H ⊥ A B$ ， $C H = h$ ， $A B = c$ ，若内接正方形 $D E F G$ 的边长是x，则h、c、x的数量关系为（）

A、 $x^{2} + h^{2} = c^{2}$ B、 $\frac{1}{2} x + h = c$ C、 $h^{2} = x c$ D、 $\frac{1}{x} = \frac{1}{h} + \frac{1}{c}$

查看试题解析

二、填空题

11. 一组数据：5，6，5，3，7的众数是.

查看试题解析
12. “若a²＝b² ，则a＝b”这一事件是.（填“必然事件”“不可能事件”或“随机事件”）

查看试题解析
13. 若关于x的一元二次方程 $x^{2} - 4 x + m - 1$ 有两个相等的实数根，则m的值为.

查看试题解析
14. 如图， $△ A B D$ 内接于 $⊙ O$ ， $∠ A D B = 90 °$ ， $∠ A D B$ 的角平分线 $D C$ 交 $⊙ O$ 于C.若 $B D = 8$ ， $B C = 5 \sqrt{2}$ ，则 $A D$ 的长为.

查看试题解析
15. 圆锥的母线长为4，底面半径为3，圆锥的侧面积为（结果保留 $π$ ）.

查看试题解析
16. 若二次函数y＝（m+1）x^|m|的图象的开口向下，则m的值为．

查看试题解析
17. 在锐角 $△ A B C$ 中， $A B = 8$ ， $∠ B = 60 °$ ， $A C = 7$ ， $∠ C = α$ ，则 $c o s α =$ .

查看试题解析
18. 二次函数 $y = \frac{1}{2} x^{2} + \frac{1}{2} x$ 的图象如图所示，点 $A_{1} 、 A_{2} 、 A_{3} 、 A_{4} 、 ⋯ ⋯ 、 A_{2022}$ 在二次函数 $y = \frac{1}{2} x^{2} + \frac{1}{2} x$ 位于第一象限的图象上，点 $B_{1} 、 B_{2} 、 B_{3} 、 B_{4} 、 ⋯ ⋯ 、 B_{2022}$ 在y轴的正半轴上， $△ O A_{1} B_{1} 、 △ B_{1} A_{2} B_{2} 、 ⋯ ⋯ 、 △ B_{2021} A_{2022} B_{2022}$ 都是等腰直角三角形，则 $B_{2021} A_{2022} =$ .

查看试题解析

三、解答题

19. 解下列方程：

(1)、 $x^{2} - 6 x + 8 = 0$ ；

(2)、 $3 x - x^{2} = x - 3$ .

查看试题解析
20. 如图，在⊙O中，AC $∥$ OB，∠BAO＝25°，求∠BOC的度数.

查看试题解析
21. 为了进一步完善“课后延时服务”，某学校额外开设了A班电影鉴赏，B班漫画漫游，C班跑步健身三门兴趣课程，小智和小慧需选择一门课程学习.

(1)、用列表法或画树状图法，列出小智、小慧两人选课所有可能出现的情况.

(2)、求小智、小慧两人同班的概率.

查看试题解析
22. 如图， $∠ B A D = ∠ C A E$ ， $∠ B = ∠ D$ .

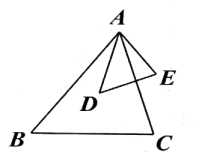(1)、 $△ A B C$ 与 $△ A D E$ 相似吗？为什么？

(2)、如果 $A B = 2 A D$ ， $B C = 4$ ，那么 $D E$ 的长为多少？

查看试题解析
23. 如图，某校教学楼（矩形 $A G H D$ ）前是办公楼（矩形 $B E N M$ ），教学楼与办公楼之间是学生活动场所（ $A B$ ）和旗杆（ $C F$ ），教学楼、办公楼和旗杆都垂直于地面，在旗杆底C处测得教学楼顶的仰角为 $45 °$ ，在旗杆底C处测得办公楼顶的俯角为 $37 °$ ，已知教学楼高度 $A D$ 为 $20 m$ ，旗杆底部（C）到办公楼底部（B）的距离比到教学楼底部（A）的距离少 $4 m$ ，求办公楼的高度 $E B$ .（参考数据 $s i n 31 ° \approx 0.60$ ， $c o s 37 ° \approx 0.80$ ， $t a n 37 ° \approx 0.75$ ）

查看试题解析
24. 某学校想了解学生家长对“双减”政策的认知情况，随机抽查了部分学生家长进行调查，将抽查的数据结果进行统计，并绘制两幅不完整的统计图（A：不太了解，B：基本了解，C：比较了解，D：非常了解）.请你根据图中提供的信息回答以下问题：

(1)、请求出这次被调查的学生家长共有多少人？

(2)、请补全条形统计图.

(3)、试求出扇形统计图中“比较了解”部分所对应的圆心角度数.

(4)、该学校共有1200名学生家长，估计对“双减”政策了解程度为“非常了解”的学生家长大约有多少？

查看试题解析
25. 如图，AB是⊙O的直径，射线BC交⊙O于点D，E是劣弧AD上一点，且 $\overset{⌢}{A E} = \overset{⌢}{D E}$ ，过点E作EF⊥BC于点F，延长FE和BA的延长线交于点G.

(1)、证明：GF是⊙O的切线；

(2)、若AG＝6，GE＝6 $\sqrt{2}$ ，求△GOE的面积.

查看试题解析
26. 2022年2月4日，第24届冬季奥林匹克运动会在北京胜利召开，在冬奥会期间，北京某校打算组织部分师生利用周日时间到现场观看比赛，经了解在离学校最近的比赛场馆当日共有A、B两场比赛，两场比赛的票价如下图所示，其中x轴表示一次性购票人数，y轴表示每张票的价格，如：一次性购买A场比赛门票10张，票价为400元/张，若一次性购买A场比赛门票80张，则每张票价为200元.

(1)、若一次性购买B场比赛门票10张，则每张票价为元（直接写出结果）.

(2)、若一次性购买A场比赛门票 $a (50 < a < 60)$ 张，需支付门票费用多少元？（用a的代数式表示）

(3)、该校共组织120人（每人购买一张门票）分两组分别观看A、B两场比赛，共花费32160元，若观看A场比赛的人数不足50人，则有多少人观看了B场比赛？

查看试题解析
27. 如图1，已知矩形 $A B C D$ 的边长 $A B = 3 c m$ ， $B C = 6 c m$ .某一时刻，动点M从点A出发，沿 $A B$ 以 $1 c m / s$ 的速度向点B匀速运动：同时点N从点D出发，沿 $D A$ 方向以 $2 c m / s$ 的速度向点A匀速运动，点N运动到点A时停止运动，运动时间为t.

(1)、若 $△ A M N$ 是等腰直角三角形，则t=（直接写出结果）.

(2)、是否存在时刻t，使以A、M、N为顶点的三角形与 $△ A C D$ 相似？若存在，求t的值，若不存在，请说明理由.

(3)、如图2，连接 $C N 、 C M$ ，试求 $C N + 2 C M$ 的最小值.

查看试题解析
28. 如图1，探照灯、汽车前灯的反光曲面都是“抛物镜面”，它是由过等腰直角三角形（ $△ A B C$ ）顶点的抛物线绕着对称轴旋转一周所形成的，我们将抛物线和线段 $A B$ 所围成的封闭图形称之为“碗形”，记作“碗形 $A B C$ ”，其中抛物线部分叫“标准线”，记作“标准线 $A C B$ ”，抛物线的顶点C称为“碗顶”，直角三角形的斜边 $A B$ 的长度称为“碗宽”，碗顶C到 $A B$ 的距离称为“碗高”.

(1)、若碗形 $A B C$ 的碗宽是 $20 c m$ ，则碗高是 $c m$ （直接写出结果）.

(2)、如图2，碗形 $A B C$ 的碗宽为4，点A与坐标原点重合，点B在x轴的正半轴上，点C在x轴下方，求标准线 $A C B$ 的函数表达式（不需要写出自变量的取值范围）

(3)、将（2）中的碗形 $A B C$ 绕点B顺时针旋转得到碗形 $A^{'} B C^{'}$ ，旋转角为 $α$ ，且 $t a n α = \frac{1}{2}$
①标准线 $A C B$ 、标准线 $A^{'} C^{'} B$ 和线段 $A A^{'}$ 围成的封闭图形的面积为（直接写出结果）.

②过点 $C^{'}$ 作 $C^{'} D ⊥ A B$ 交 $A B$ 于点D，交 $A^{'} B$ 于点F.试求 $\frac{F D}{D C^{'}}$ 的值.

查看试题解析