江苏省宿迁市泗洪县2022年中考数学一模试题

试卷更新日期：2022-05-07 类型：中考模拟

进入出卷网下载

一、单选题

1. -2的相反数是（）

A、 $- 2$ B、2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. （﹣2）³=（　　）

A、﹣6 B、6 C、﹣8 D、8

查看试题解析
3. 下列图形中既是轴对称图形又是中心对称图形的是( )

A、正六边形 B、正五边形 C、平行四边形 D、等腰三角形

查看试题解析
4. 圆内接四边形ABCD，∠A，∠B，∠C的度数之比为3∶4∶6，则∠D的度数为(　　)

A、60° B、80° C、100° D、120°

查看试题解析
5. 有9名同学参加歌咏比赛，他们的预赛成绩各不相同，现取其中前4名参加决赛，小红同学在知道自己成绩的情况下，要判断自己能否进入决赛，还需要知道这9名同学成绩的（）

A、众数 B、中位数 C、平均数 D、极差

查看试题解析
6. 抛掷一枚质地均匀的普通骰子2次，朝上一面的点数之和可能为2，3，4，5，6，7，8，9，10，11，12，其中概率最大的是（　　）

A、5 B、6 C、7 D、8

查看试题解析
7. 已知二元一次方程组 ${\begin{array}{l} | x | + x + y = 10 \\ x + | y | - y = 12 \end{array}$ ，则x+y的值等于（　　）

A、﹣2 B、 $\frac{18}{5}$ C、9 D、22

查看试题解析
8. 已知二次函数 $y = x^{2} + b x + c$ 中，其函数y与自变量x的部分对应值如下表所示：
$x$
…
0
1
2
3
…
$y$
…
5
2
1
2
…
点 $A (x_{1} ， y_{1})$ 、 $B (x_{2} ， y_{2})$ 在函数的图象上，当 $0 < x_{1} < 1$ 、 $2 < x_{2} < 3$ 时， $y_{1}$ 与 $y_{2}$ 的大小关系是（）

A、 $y_{1} \geq y_{2}$ B、 $y_{1} \leq y_{2}$ C、 $y_{1} > y_{2}$ D、 $y_{1} < y_{2}$

查看试题解析

二、填空题

9. 因式分解： $a x^{2} - 2 a x + a =$ .

查看试题解析
10. 在函数 $y = \frac{\sqrt{x - 2}}{x - 3}$ 中，自变量x的取值范围是.

查看试题解析
11. 如图，大圆的弦AB切小圆于点C，且大圆的半径为5cm，小圆的半径为3cm，则弦AB的长为 cm.

查看试题解析
12. 已知x＝﹣2时，二次三项式x²﹣2mx+4的值等于﹣4，当x＝时，这个二次三项式的值等于﹣1.

查看试题解析
13. 一箱饮品（每箱12瓶）中有2瓶的盖内印有“奖”字，小明的爸爸买了一箱这种品牌的饮品，但连续打开2瓶均未中奖，此时小明在剩下的饮品中任意拿一瓶，那么他拿出的这瓶饮品中奖的机会是 .

查看试题解析
14. 某工厂两年内产值翻了一番，则该工厂产值年平均增长的百分率等于 .（结果精确到0.1%，参考数据： $\sqrt{2} \approx$ 1.414， $\sqrt{3} \approx$ 1.732.）

查看试题解析
15. 已知抛物线 $y = a x^{2} + b x + c$ 的对称轴是直线 $x = - 1$ .若关于x的一元二次方程 $a x^{2} + b x + c = 0$ 的一个根为4，则该方程的另一个根为.

查看试题解析
16.
如图所示，每个小正方形的边长为1，A、B、C是小正方形的顶点，则∠ABC的度数为

查看试题解析
17. 如图，在矩形ABCD中，AB＝2，BC＝3，在边BC上取点P，使∠DAP的平分线过DC的中点Q，则线段BP的长等于 .

查看试题解析
18. 已知△ABC的边长都是关于x的方程x²﹣3 $\sqrt{k}$ x+8＝0的解，其中整数k＜5，则△ABC的周长等于 .

查看试题解析

三、解答题

19. 已知：a $= \sqrt{5} +$ 2，b $= \sqrt{5} -$ 2，求（a+b）（a²+b²﹣ab）的值.

查看试题解析
20. 解下列方程：

(1)、（2x+1）（x﹣3）＝0；

(2)、 $x^{2} - 4 \sqrt{2} x + 8 = 0$ .

查看试题解析
21. 小明所在的数学兴趣小组共10名学生，在一次数学知识拓展测试中，全组的平均得分是88分，除小明外，另9名同学的得分如表（单位：分）：
得分
97
91
88
86
85
84
82
人数
1
2
1
1
2
1
1

(1)、小明得分是多少？

(2)、求该小组此次测试得分的方差.

查看试题解析
22. 如图，在四边形ABCD中，AD∥BC，AD＝2，AB＝2 $\sqrt{2}$ ，以点A为圆心，AD为半径的圆与BC相切于点E，交AB于点F.若扇形AFD是一个圆锥的侧面，求这个圆锥的底面圆的半径.

查看试题解析
23. 把二次函数y＝x²+bx+c的图象向下平移1个单位长度，再向左平移5个单位长度，所得的抛物线顶点坐标为（﹣3，2），求原抛物线相应的函数表达式.

查看试题解析
24. 小明和小丽在做一个“配紫色”游戏：一个不透明的袋子中装有1个白球，1个蓝球和2个红球，它们除颜色外都相同.从中摸出2个球，若一个是红色，一个是蓝色，则可以配成紫色，游戏获胜、搅匀后，小明从中任意摸出一个球，记录颜色后放回、搅匀，再从中任意摸出一个球；搅匀后，小丽从中任意摸出1个球（不放回），再从余下的3个球中任意摸出1个球.这个游戏公平吗？为什么？

查看试题解析
25. 我们知道，可以借助于函数图象求方程的近似解.如图（甲），把方程x﹣2＝1﹣x的解看成函数y＝x﹣2的图象与函数y＝1﹣x的图象的交点的横坐标，求得方程x﹣2＝1﹣x的解为x＝1.5.

(1)、如图（乙），已画出了反比例函数 $y = \frac{1}{x}$ 在第一象限内的图象，借助于此图象求出方程2x²﹣2x﹣1＝0的正数解.（要求画出相应函数的图象，结果精确到0.1）

(2)、选择：三次方程x³﹣x²﹣2x+1＝0的根的正负情况是　　.

A、有两个负根，一个正根 B、有三个负根 C、有一个负根，两个正根 D、有三个正根

查看试题解析
26. 如图， $A B$ 是 $⊙ O$ 的直径，点P是 $⊙ O$ 外一点， $P A$ 切 $⊙ O$ 于点A，连接 $O P$ ，过点B作 $B C ∥ O P$ 交 $⊙ O$ 于点C，点E是 $\overset{⌢}{A B}$ 的中点，且 $A B ＝ 10 ， B C ＝ 6$ .

(1)、 $P C$ 与 $⊙ O$ 有怎样的位置关系？为什么？

(2)、求 $C E$ 的长.

查看试题解析
27. 某种蔬菜在3﹣6月份的销售单价与销售月份之间的关系如图（甲）所示，成本与销售月份之间的关系如图（乙）所示.（图（甲）中4个点在一条直线上，图（乙）中的4个点在一条抛物线上）

(1)、求该蔬菜5月份的销售单价.（精确到0.1元）

(2)、求该蔬菜4月份每千克的成本.（精确到0.1元）

(3)、哪个月出售这种蔬菜，每千克的收益最大？每千克的最大收益是多少元？（收益＝售价﹣成本）

查看试题解析
28.
如图，已知抛物线m：y=ax²﹣6ax+c（a＞0）的顶点A在x轴上，并过点B（0，1），直线n：y=﹣ $\frac{1}{2}$ x+ $\frac{7}{2}$ 与x轴交于点D，与抛物线m的对称轴l交于点F，过B点的直线BE与直线n相交于点E（﹣7，7）．

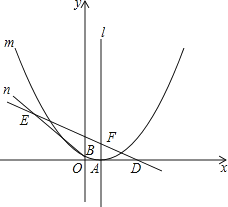(1)、求抛物线m的解析式；

(2)、P是l上的一个动点，若以B，E，P为顶点的三角形的周长最小，求点P的坐标；

(3)、抛物线m上是否存在一动点Q，使以线段FQ为直径的圆恰好经过点D？若存在，求点Q的坐标；若不存在，请说明理由．

查看试题解析

$x$	…	0	1	2	3	…
$y$	…	5	2	1	2	…

得分	97	91	88	86	85	84	82
人数	1	2	1	1	2	1	1