河南省驻马店市上蔡县2022年中招质量检测数学试卷

试卷更新日期：2022-05-07 类型：中考模拟

进入出卷网下载

一、单选题

1. 0， $- 1$ ， 2， $- \frac{2021}{2022}$ 这四个数中，最小的数是（）

A、0 B、 $- 1$ C、2 D、 $- \frac{2021}{2022}$

查看试题解析
2. 据新华社报道，截至2021年10月，全国冰雪运动参与人数达到3.46亿.将数据“3.46亿”用科学记数法表示为（）

A、 $3.46 \times 1 0^{7}$ B、 $3.46 \times 1 0^{8}$ C、 $0.346 \times 1 0^{9}$ D、 $34.6 \times 1 0^{7}$

查看试题解析
3. 如图，该几何体由6个大小相同的小正方体堆成，则该几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
4. 下列运算正确的是（）

A、 $3 m n - 2 m = n$ B、 ${(- 3 m)}^{2} = 6 m^{2}$ C、 ${(m + n)}^{2} = m^{2} + n^{2}$ D、 $2 m^{2} \cdot 3 m = 6 m^{3}$

查看试题解析
5. 如图， $a ∥ b$ ，点A在直线b上，点C在直线a上， $A B ⊥ B C$ .若 $∠ 2 = 140 °$ ，则∠1的度数为（）

A、140° B、130° C、120° D、150°

查看试题解析
6. 下列方程有两个相等的实数根的是（）

A、 $x^{2} + 1 = 0$ B、 $x^{2} + x = 0$ C、 $x^{2} + x + 1 = 0$ D、 $x^{2} + 2 x + 1 = 0$

查看试题解析
7. 某班级男生在体育课上进行投篮测试，每人投10次.他们投中的次数统计如下表：
投中次数
5
6
7
8
9
10
人数
2
4
5
10
3
1
则该班级男生在此次测试中投中次数的中位数、众数分别是（）

A、8，8 B、7.5，7 C、8，7 D、7，8

查看试题解析
8. 如图，直线AB经过原点O，且交反比例函数 $y = \frac{k}{x}$ 的图象于点B，A，点C在x轴上，且 $B C = \frac{1}{2} B A$ .若 $S_{△ B C A} = 12$ ，则k的值为（）

A、12 B、 $- 12$ C、 $- 6$ D、6

查看试题解析
9. 如图，在矩形ABCD中，原点O为其对角线BD的中点， $A B ∥ y$ 轴，点C的坐标为 $(2 ， - 1)$ ，将 $△ A B D$ 沿BD方向平移得到 $△ A^{'} B^{'} D^{'}$ ，当点 $A^{'}$ 在y轴上时，点 $D^{'}$ 的坐标为（）

A、 $(3 ， 2)$ B、 $(2 \sqrt{5} ， \sqrt{5})$ C、 $(3 ， 4)$ D、 $(4 ， 2)$

查看试题解析
10. 如图，在菱形ABCD中， $∠ B = 60 °$ ， $A B = 2$ ，以点D为圆心，CD长为半径作 $\overset{⌢}{C A}$ ，分别以点A，D为圆心，大于 $\frac{1}{2} A D$ 的长为半径作孤，两弧交于点E，作直线CE，F为菱形内部直线CE上一点，连接AF，DF，AC.若 $∠ A F D = 90 °$ ，则阴影部分的面积为（）

A、 $\frac{2}{3} π - \frac{\sqrt{3} + 1}{2}$ B、 $\frac{2}{3} π - \frac{\sqrt{3} - 1}{2}$ C、 $π - \frac{\sqrt{3} + 1}{2}$ D、 $\frac{2}{3} π + \frac{\sqrt{3} + 1}{2}$

查看试题解析

二、填空题

11. 计算： $\sqrt[3]{- 8} + {(- \sqrt{2022})}^{0} + {(- 1)}^{- 1} =$ .

查看试题解析
12. 写一个函数解析式，使其图象经过第一、二、三象限，且在第三象限内函数值随自变量的增大而增大，则这个函数解析式可以是.

查看试题解析
13. 一个不透明的袋子里装着2个红球，3个白球，它们除了颜色不同以外，其他完全相同.若从袋子里随机摸出一个球，不放回，再从袋子里摸出一个球，两次摸到的球恰好颜色相同的概率为.

查看试题解析
14. 若将三个如图1所示的直角三角形拼成如图2所示的图形，在图2中标记字母，并连接AE，CD，G，H分别为AE，CD的中点，连接GH，如图3所示.若 $A C = 2$ ，则GH的长为.

查看试题解析
15. 如图，在平行四边形ABCD中，对角线AC，BD相交于点O， $∠ B C D = 45 °$ ， $A B = B D = 6$ ， E为AD上一动点，连接BE，将 $△ A B E$ 沿BE折叠得到 $△ F B E$ ，当点F落在平行四边形的对角线上时，OF的长为.

查看试题解析

三、解答题

16.

(1)、化简： $(x - \frac{4 x - 4}{x}) \div \frac{x - 2}{x}$ .

(2)、解不等式组： ${\begin{array}{l} 2 (x - 1) > x + 1 ① \\ 1 - \frac{2 x + 5}{3} \leq x - \frac{7}{3} ② \end{array}$

查看试题解析
17. 某学校为了解学生关于新冠病毒防疫常识的掌握情况，特开展了网络防疫测试.某小组随机抽取部分学生的测试成绩x（满分100分），并进行整理分析，绘制了如下尚不完整的统计图表.
学生测试成绩频数分布表
组别
成绩x/分
人数
A
$60 \leq x < 70$
n
B
$70 \leq x < 80$
9
C
$80 \leq x < 90$
12
D
$90 \leq x \leq 100$
6
根据以上信息，回答下列问题：

(1)、本次共抽取了名学生的测试成绩.

(2)、m= ， n=.

(3)、若成绩低于80分，视为对防疫常识了解不到位，根据以上信息，分析学生对防疫常识的了解情况，并向学校提出合理化建议.

查看试题解析
18. 如图，在 $△ B C D$ 中， $B D = C D$ ，以BC为直径作⊙O，交BD于点E，交CD于点F，连接EF，BG平分 $∠ F B C$ ，交⊙O于点G，GH为⊙O的切线，交BC的延长线于点H.

(1)、求证： $D E = D F$ .

(2)、若⊙O的直径为10， $C H = 1$ ，求BE的长.

查看试题解析

19. 为了测量学校旗杆（垂直于水平地面）的高度，班里三个兴趣小组设计了三种不同的测量方案，如下表所示.

课题	测量校园旗杆的高度
测量工具	测角仪（测量角度的仪器），卷尺，平面镜等
测量小组	A组	B组	C组
测量方案示意图
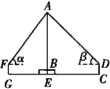
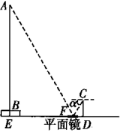
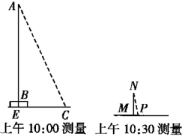
说明	线段AB表示旗杆的高度，线段BE表示旗杆底座高度，点A，B，E共线，线段CD，FG表示测角仪的高度，点A，B，C，D，E，F，G在同一竖直平面内，CG表示两次测角仪摆放位置的距离，测角仪可测得旗杆顶端A的仰角	线段AB表示旗杆的高度，线段BE表示旗杆底座高度，点A，B，E共线，线段CD表示测角仪的高度，DE表示测角仪到旗杆的距离，点F表示平面镜的中心，点E，F，D共线，眼睛在C处，移动平面镜，看向中心F，恰好看到旗杆顶端A，此时用测角仪测得平面镜的俯角，A，B，C，D，E，F六点在同一竖直平面内	线段AB表示旗杆的高度，线段BE表示旗杆底座高度，点A，B，E共线，EC为旗杆与底座某一时刻下的影长，A，B，C，E四点在同一竖直平面内，标杆NM垂直于水平地面，PM为标杆NM在某一时刻的影长
测量数据	$α$ 为 $53 °$ ， $β$ 为 $45 °$ ， $C D = F G = 1.5$ 米， $B E = 0.5$ 米， $C G = 14.79$ 米	$D E = 6.61$ 米， $C D = 1.5$ 米， $B E = 0.5$ 米， $α$ 为 $60 °$	$C E = 4.66$ 米， $M N = 1$ 米， $M P = 0.21$ 米， $B E = 0.5$ 米

(1)、上述A，B，C三个小组中，用哪个小组测量的数据计算出的旗杆高度不是旗杆的真实高度，为什么？

(2)、请结合所学知识，利用A组测量的数据计算出旗杆的高度AB.（结果保留两位小数.参考数据：

t a n 53 ° \approx \frac{4}{3}

，

\sqrt{3} \approx 1.732

）

查看试题解析

20. 某校需要购进一批消毒液，经了解，某商场供应A，B两种类型的消毒液.购买2瓶A类型消毒液所需费用和3瓶B类型消毒液所需费用相同；购头3瓶A类型消毒液和1瓶B类型消毒液共需要55元.

(1)、求A，B两种类型消毒液的单价.

(2)、若根据需求，需要购买A，B两种类型消毒液共300瓶，其中A类型消毒液的数量不少于B类型消毒液数量的 $\frac{1}{2}$ ，如何购买才能使得花费最少，最少花费为多少元？

查看试题解析
21. 在学完二次函数的图象与性质后，某数学兴趣小组对函数 $y = \frac{x^{2} - 1}{x^{2} + 1}$ 的图象与性质进行了探究，下面是该兴趣小组的探究过程，请补充完整：

(1)、列表
x
…
$- 3$
$- 2$
$- 1$
$- 0.75$
$- 0.5$
$- 0.25$
0
0.25
0.5
0.75
1
2
3
…
y
…
$\frac{4}{5}$
$\frac{3}{5}$
0
$- \frac{7}{25}$
$- \frac{3}{5}$
$- \frac{15}{17}$
a
$- \frac{15}{17}$
$- \frac{3}{5}$
$- \frac{7}{25}$
0
$\frac{3}{5}$
$\frac{4}{5}$
…
表格中a的值为.

(2)、描点，连线，根据以上信息将函数图象补充完整.

(3)、观察函数图象，请写出此函数的两条性质：
①；
②.

(4)、已知关于x的方程 $\frac{x^{2} - 1}{x^{2} + 1} = m$
①若方程有两个相等的实数根，则m的值为；
②若方程有两个不相等的实数根，则m的取值范围为.

查看试题解析
22. 如图，在平面直角坐标系 $x O y$ 中， $A (1 ， 2)$ ， $B (- 3 ， 1)$ .已知抛物线 $y = a x^{2} + 4 a x - 5$ .

(1)、求抛物线的对称轴.

(2)、若当 $- 3 \leq x \leq 1$ 时，函数的最大值为10，求a的值.

(3)、若抛物线的顶点在 $△ A O B$ 的内部（不含边界），求a的取值范围.

查看试题解析
23. 如图，在 $△ A B C$ 中， $∠ B = α$ ， $A B = A C$ ， O为BC的中点，D为AB上一点，作直线DO，过点A作 $A E ⊥ D O$ 于点E，过点C作 $C F ⊥ D O$ 于点F.

(1)、如图1，当 $α = 45 °$ 时，EF，AE和CF的数量关系为.

(2)、如图2，若 $0 ° < α < 90 °$ 时，请求出EF，AE和CF的数量关系（用含 $α$ 的三角函数值的式子表示）.

(3)、若 $α = 30 °$ ， $B C = 2 \sqrt{3}$ ，当 $E F ⊥ A B$ 时，直接写出CD的长.

查看试题解析

组别	成绩x/分	人数
A	$60 \leq x < 70$	n
B	$70 \leq x < 80$	9
C	$80 \leq x < 90$	12
D	$90 \leq x \leq 100$	6

x	…	$- 3$	$- 2$	$- 1$	$- 0.75$	$- 0.5$	$- 0.25$	0	0.25	0.5	0.75	1	2	3	…
y	…	$\frac{4}{5}$	$\frac{3}{5}$	0	$- \frac{7}{25}$	$- \frac{3}{5}$	$- \frac{15}{17}$	a	$- \frac{15}{17}$	$- \frac{3}{5}$	$- \frac{7}{25}$	0	$\frac{3}{5}$	$\frac{4}{5}$	…

投中次数	5	6	7	8	9	10
人数	2	4	5	10	3	1