河南省中考信阳市部分重点中学2022年第一次联合摸底数学试卷

试卷更新日期：2022-05-07 类型：中考模拟

进入出卷网下载

一、单选题

1. $\sqrt{9}$ 的相反数是（）

A、 $\frac{1}{9}$ B、-3 C、-9 D、 $- \frac{1}{3}$

查看试题解析
2. 聪聪在阅读一篇文章时看到水分子的直径约为0.4纳米，通过百度搜索聪聪又知道1纳米 $= 10^{- 9}$ 米，则水分子的直径约为（）

A、 $4 \times 10^{- 10}$ 米 B、 $0.4 \times 10^{- 10}$ 米 C、 $4 \times 10^{- 9}$ 米 D、 $4 \times 10^{- 8}$ 米

查看试题解析
3. 如图，胶带的左视图是（）

A、 B、 C、 D、

查看试题解析
4. 如图，将矩形纸带ABCD沿直线EF折叠，A，D两点分别与 $A^{'}$ ， $D^{'}$ 对应.若 $∠ 1 = 2 ∠ 2$ ，则 $∠ A E F$ 的度数为（）

A、60° B、65° C、72° D、75°

查看试题解析
5. 下列运算正确的是（）

A、（xy³）²＝xy⁶ B、 $\sqrt{8} + \sqrt{2} = 4 \sqrt{2}$ C、2x¹²÷x⁶＝2x⁶ D、（a﹣3）²＝a²﹣9

查看试题解析
6. 在对一组样本数据进行分析时，小华列出了方差的计算公式S²＝ $\frac{(5 - \bar{x})^{2} + (4 - \bar{x})^{2} + (4 - \bar{x})^{2} + (3 - \bar{x})^{2} + (3 - \bar{x})^{2}}{5}$ ，下列说法错误的是（）

A、样本容量是5 B、样本的中位数是4 C、样本的平均数是3.8 D、样本的众数是4

查看试题解析
7. 定义运算：a※b＝3ab²﹣4ab﹣2.例如：4※2＝3×4×2²﹣4×4×2﹣2＝14.则方程2※x＝0的根的情况为（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、无法确定

查看试题解析
8. 已知点A（﹣1，6），B（m，y₁），C（m+1，y₂）在反比例函数y＝ $\frac{k}{x}$ 的图象上，若m＞0，则y₁ ， y₂的大小关系是（）

A、y₁＞y₂＞6 B、y₁＜y₂＜6 C、y₁＝y₂＝6 D、无法确定

查看试题解析
9. 如图，在 $R t Δ A B C$ 中， $∠ A C B = 90^{\circ}$ ，以点 $A$ 为圆心， $A C$ 的长为半径作弧交 $A B$ 于点 $D$ ，再分别以点 $C$ ， $D$ 为圆心，大于 $\frac{1}{2} C D$ 的长为半径作弧，两弧交于点 $P$ ，作射线 $A P$ 交 $B C$ 于点 $E$ ．若 $A C = 3$ ， $B C = 4$ ，则 $\frac{C E}{B E}$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{3}{5}$ C、 $\frac{3}{4}$ D、 $\frac{4}{5}$

查看试题解析
10. 如图，等边 $△ A B C$ 的顶点 $A (1 ， 1)$ ， $B (3 ， 1)$ ；规定把 $△ A B C$ “先沿x轴翻折，再向左平移1个单位”为一次变换，这样连续经过2021次变换后，等边 $△ A B C$ 的顶点C的坐标为（）.

A、 $(- 2020 ， \sqrt{3} + 1)$ B、 $(- 2017 ， - \sqrt{3} - 1)$ C、 $(- 2018 ， \sqrt{3} + 1)$ D、 $(- 2019 ， - \sqrt{3} - 1)$

查看试题解析

二、填空题

11. 写出一个比 $\sqrt{7}$ 大比 $\sqrt{11}$ 小的整数.

查看试题解析
12. 不等式组 ${\begin{array}{l} 5 x - 2 > 3 x - 4 \\ \frac{1}{3} x \geq x - \frac{2}{3} \end{array}$ 的最大整数解为.

查看试题解析
13. 为了解某区六年级8400名学生中会游泳的学生人数，随机调查了其中400名学生，结果有150名学生会游泳，那么估计该区会游泳的六年级学生人数约为．

查看试题解析
14. 如图，在扇形AOB中，∠AOB=90°，OA=4，以OB为直径作半圆，圆心为点C，过点C作OA的平行线分别交两弧点D、E，则阴影部分的面积为.

查看试题解析
15. 如图，直线 $y = - x + 4$ 与坐标轴分别交于 $A ， B$ 两点， $O C ⊥ A B$ 于点C，P是线段 $O C$ 上一个动点，连接 $A P$ ，将线段 $A P$ 绕点A逆时针旋转45°，得到线段 $A P^{^{'}}$ ，连接 $C P^{'}$ ，则线段 $C P^{'}$ 的最小值为

查看试题解析

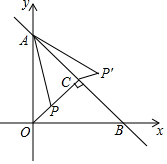
三、解答题

16. 下面是小明同学进行分式化简的过程，请认真阅读并完成相应任务.
$(\frac{a^{2} - 1}{a^{2} + 2 a + 1} + 1) \div \frac{a}{a + 1} = [\frac{(a + 1) (a - 1)}{(a + 1)^{2}} + 1] \div \frac{a}{a + 1}$ （第一步）

＝ $(\frac{a - 1}{a + 1} + 1) \div \frac{a}{a + 1}$ （第二步）

＝ $\frac{a - 1 + 1}{a + 1} \div \frac{a}{a + 1}$ （第三步）

＝ $\frac{a}{a + 1} \times \frac{a + 1}{a}$ （第四步）

＝1（第五步）.

(1)、任务一：填空：

①第一步进行的运算是（填序号）；

A、整式乘法.

B、因式分解.

②第步开始出现错误，这一步错误的原因是.

(2)、任务二：请直接写出该分式化简的正确的结果；

(3)、任务三：请根据平时数学的学习经验，就分式的化简过程写出一条注意事项.

查看试题解析
17. 为监控某条生产线上产品的质量，检测员每隔相同时间抽取一件产品，并测量其长度，在一天的抽检结束后，检测员将测得的各数据按从小到大的顺序整理成如下表格：
编号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
长度（cm）
8.72
8.88
8.92
8.93
8.94
8.96
8.97
8.98
a
9.03
9.04
9.06
9.07
9.08
b
按照生产标准，产品等次规定如表：
长度（单位：cm）
产品等次
$8.97 \leq x \leq 9.03$
特等品
$8.95 \leq x \leq 9.05$
优等品
$8.90 \leq x \leq 9.10$
合格品
$x < 8.90$ 或 $x > 9.10$
非合格品
注：在统计优等品个数时，将特等品计算在内；在统计合格品个数时，将优等品（含特等品）计算在内.

(1)、已知此次抽检产品的合格率为80%，则非合格品有个.

(2)、已知此次抽检出的优等品长度的中位数为9 $c m$ .
①求a的值：
②将这些优等品分成两组，一组长度大于9 $c m$ ，另一组长度不大于9 $c m$ ，从这两组中各随机抽取1件进行复检，求抽到的2件产品都是特等品的概率.

查看试题解析
18. 如图，某工地有一辆吊车， $A B$ 为车身， $A C$ 为吊臂，吊车从水平地面C处吊起货物，此时测得吊臂 $A C$ 与水平线的夹角为 $18 °$ .当货物吊至D处时，测得吊臂 $A D$ 与水平线的夹角为 $53 °$ ，且吊臂转动过程中长度始终保持不变，此时D处离水平地面的高度 $D E = 12 m$ ，求吊臂的长.（结果保留一位小数，参考数据： $\sin 18 ° \approx 0.30$ ， $\cos 18 ° \approx 0.95$ ， $\tan 18 ° \approx 0.32$ ， $\sin 53 ° \approx 0.80$ ， $\cos 53 ° \approx 0.60$ ， $\tan 53 ° \approx 1.33$ ）

查看试题解析
19. 已知 $△ A B C$ 是⊙O的内接三角形， $A B$ 为⊙O的直径.点D是⊙O外一点，连接 $A D$ 和 $O D$ ， $O D$ 与 $A C$ 相交于点E，且 $O D ⊥ A C$ .

(1)、如图1，若 $A D$ 是⊙O的切线， $t a n ∠ B A C = \frac{1}{2}$ ，证明： $A D = A B$ ；

(2)、如图2，延长 $D O$ 交⊙O于点F，连接 $C D$ ， $C F$ ， $A F$ .当四边形 $A D C F$ 为菱形，且 $∠ B A C = 30 °$ ， $B C = 1$ 时，求 $D F$ 的长.

查看试题解析
20. 某文具店准备购进A、B两种品牌的文具袋进行销售，若购进A品牌文具袋和B品牌文具袋各5个共花费120元，购进A品牌文具袋3个和B品牌文具袋4个共花费88元.

(1)、求购进A品牌文具袋和B品牌文具袋的单价；

(2)、若该文具店购进了A，B两种品牌的文具袋共100个，其中A品牌文具袋售价为12元，B品牌文具袋售价为23元，设购进A品牌文具袋x个，获得总利润为w元.
①求w关于x的函数关系式；

②要使销售文具袋的利润最大，且所获利润不低于进货价格的45%，请你帮该文具店设计一个进货方案，并求出其所获利润的最大值.

查看试题解析
21. 已知抛物线 $y = a x^{2} - 2 a x - 2 + 3 a^{2}$ .

(1)、求该抛物线的对称轴；

(2)、若该抛物线的顶点在x轴上，求其解析式；

(3)、当 $a > 0$ 时，若 $A (m - 1 ， y_{1}) ， B (1 ， y_{2}) ， C (m + 2 ， y_{3})$ 为该抛物线上三点，且总有 $y_{1} > y_{3} > y_{2}$ ，请结合图象直接写出m的取值范围.

查看试题解析

22. 小航在学习中遇到这样一个问题：

如图，点C是 $\overset{⌢}{A B}$ 上一动点，直径 $A B = 8 c m$ ，过点C作 $C D ∥ A B$ 交 $\overset{⌢}{A B}$ 于点D，O为AB的中点，连接OC，OD，当 $△ O C D$ 的面积为 $3.5 c m^{2}$ 时，求线段CD的长.

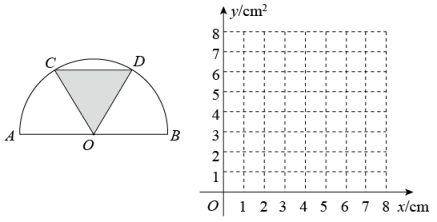
小航结合学习函数的经验探究此问题，请将下面的探究过程补充完整：

(1)、根据点C在

\overset{⌢}{A B}

上的不同位置，画出相应的图形，测量、计算线段CD的长度和

△ O C D

的面积

S_{△ O C D}

得到下表的几组对应值（当点C与点A或点B重合时，

△ O C D

的面积为0）.

$C D / c m$	0	1.0	2.0	3.0	4.0	5.0	6.0	7.0	8.0
$S_{△ O C D} / c m^{2}$	0	2.0	3.9	5.6	m	7.8	7.9	6.8	0

填空：m=.（结果保留一位小数，参考数据： $\sqrt{2} \approx 1.414$ ， $\sqrt{3} \approx 1.732$ ）

(2)、将线段CD的长度作为自变量x（cm），

△ O C D

的面积是x的函数，记为

y (c m^{2})

，请在如下平面直角坐标系xOy中画出y关于x的函数图象，并根据图象判断下列说法是否正确.（正确的打“√”，错误的打“×”）

①该函数图象为抛物线的一部分；（）

②当 $x > 3$ 时，y随x的增大而增大；（）

③ $△ O C D$ 的面积有最大值.（）

(3)、继续在同一坐标系中画出所需的图象，并结合图象直接写出：当

△ O C D

的面积为

3.5 c m^{2}

时，线段CD长度的近似值.（结果保留一位小数）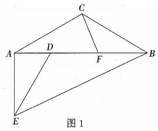

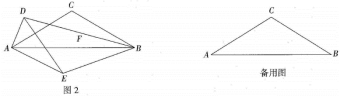查看试题解析

23. 在 $△ A B C$ 中， $A C = B C = \sqrt{3}$ ， $∠ A C B = 120 °$ ，在 $△ A D E$ 中， $∠ D A E = 90 °$ ， $∠ A E D = 30 °$ ， $A D = 1$ ，连接 $B D$ ， $B E$ ，点 $F$ 是 $B D$ 的中点，连接 $C F$ .

(1)、如图1，当顶点 $D$ 在边 $A B$ 上时，线段 $B E$ 与线段 $C F$ 的数量关系是，线段 $B E$ 与线段 $C F$ 的位置关系是；

(2)、将 $△ A D E$ 绕点 $A$ 旋转，转到图2的位置时，（1）中结论是否仍然成立？若成立，请给予证明，若不成立，请说明理由；

(3)、在 $△ A D E$ 绕点 $A$ 旋转的过程中，线段 $A F$ 的最大值为；当 $D E // C F$ 时，线段 $C F$ 的长为.

查看试题解析

编号	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
长度（cm）	8.72	8.88	8.92	8.93	8.94	8.96	8.97	8.98	a	9.03	9.04	9.06	9.07	9.08	b

长度（单位：cm）	产品等次
$8.97 \leq x \leq 9.03$	特等品
$8.95 \leq x \leq 9.05$	优等品
$8.90 \leq x \leq 9.10$	合格品
$x < 8.90$ 或 $x > 9.10$	非合格品