2022年甘肃省兰州市中考数学模拟试卷一（5月份）

试卷更新日期：2022-05-07 类型：中考模拟

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列运算正确的是（）

A、 $\sqrt{3} + 3 = 3 \sqrt{3}$ B、 $4 \sqrt{2} - \sqrt{2} = 4$ C、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ D、 $3 \sqrt{3} - \sqrt{3} = 2 \sqrt{3}$

查看试题解析
2. 观察一列数： $\frac{1}{2} ， - \frac{3}{4} ， \frac{5}{6} ， - \frac{7}{8}$ ， …，按此规律，这一列数的第2022个数是（）

A、 $- \frac{4043}{4044}$ B、 $\frac{4043}{4044}$ C、 $\frac{2022}{4044}$ D、 $\frac{2023}{4044}$

查看试题解析
3. 如图，大矩形分割成五个小矩形，④号、⑤号均为正方形，其中⑤号正方形边长为1．若②号矩形的长与宽的差为2，则知道哪个小矩形的周长，就一定能算出这个大矩形的面积（）

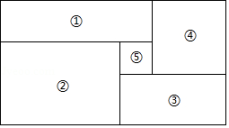A、①或③ B、② C、④ D、以上选项都可以

查看试题解析

4. 2022年2月20日，北京冬奥会圆满闭幕，冬奥会的部分金牌榜如表所示，榜单上各国代表团获得的金牌数的众数为（）

代表团	挪威	德国	中国	美国	瑞典	荷兰	奥地利
金牌数	16	12	9	8	8	8	7

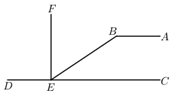
A、9 B、8.5 C、8 D、7

查看试题解析

5. 从-4，-3，1，3，4这五个数中，随机抽取一个数，记为m，若使得关于x，y的二元一次方程组 ${\begin{cases} 2 x + y = 2 \\ m x - 2 y = - 3 \end{cases}$ 有解，且使关于x的分式方程 $\frac{1 - m}{x - 1} - 1 = \frac{2}{1 - x}$ 有正数解，那么这五个数中所有满足条件的m的值之和是（）

A、1 B、2 C、-1 D、-2

查看试题解析
6. 如图所示，长方形中放入5张长为x，宽为 $y$ 的相同的小长方形，其中A，B，C三点在同一条直线上．若阴影部分的面积为52，大长方形的周长为36，则一张小长方形的面积为（）

A、3 B、4 C、5 D、6

查看试题解析
7. 下列命题不正确的是（）

A、连接直线外一点与直线上各点的所有线段中，垂线段最短 B、在同一平面内，两条不重合的直线位置关系不平行必相交 C、两点确定一条直线 D、过一点有且只有一条直线与已知直线垂直

查看试题解析
8. 如图，△ABC是等边三角形，P是三角形内一点，PD∥AB，PE∥BC，PF∥AC，若△ABC的周长为24，则PD+PE+PF＝（）

A、8 B、9 C、12 D、15

查看试题解析
9. 如图是二次函数图象的y=ax²+bx+c一部分，图象过点A（-3，0），对称轴为直线x=-1。则以下结论错误的是（）

A、b²>4ac B、2a+b=0 C、a+b+c=0 D、5a<b

查看试题解析
10. 如图， ▱ABCD的顶点A，D分别在直角∠MON的两边OM，ON上运动（不与点O重合），▱ABCD的对角线AC，BD相交于点P，连接OP，若OP=5，则▱ABCD的周长最小值是（）

A、20 B、25 C、10 D、15

查看试题解析

二、填空题（每题2分，共16分）

11. 计算 $4 x \cdot (- 3 x y^{2}) =$ .

查看试题解析
12. 若m是方程x²-3x+1=0的一个根，则3m²-9m+2022的值为

查看试题解析
13. 不透明袋子中装有1个红球，5个黑球，4个白球，这些球除颜色外无其他差别，从袋子中随机摸出一个球，则摸出红球的概率是．

查看试题解析
14. 若素数p，使得 $4 p^{2} + p + 81$ 是一个完全平方数，则p=.（若一个数能表示成某个整数的平方的形式，则称这个数为完全平方数.）

查看试题解析
15. 如图，AB∥CD，∠ABE＝148°，FE⊥CD于E，则∠FEB的度数是度．

查看试题解析
16. 公园新增设了一台滑梯，该滑梯高度AC=2米，滑梯AB的坡比是1：2，则该滑梯AB的长是米．

查看试题解析
17. 如图，已知 $A$ 为反比例函数 $y = \frac{k}{x} (k > 0)$ 图象上一点， $B$ 为 $x$ 轴正半轴上一点，过点 $B$ 作 $BC ⊥ x$ 轴交反比例函数图象于点 $C$ ，连结 $OA$ ， $AB$ ， $OC .$ 当 $OA = AB$ ， $△ DBC$ 的面积等于2时， $k$ 的值为.

查看试题解析
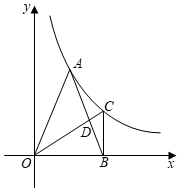18. 如图，在平面直角坐标系中，一动点从原点O出发，按向上、向右、向下、向右的方向依次平移，每次移动一个单位，得到点A₁(0，1)，A₂(1，1)，A₃(1，0)，A₄(2，0)，…那么点A₂₀₂₂的坐标为.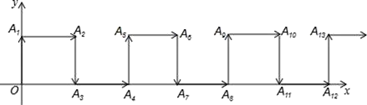

查看试题解析

三、解答题（共9题，共74分）

19.

(1)、计算： $4 cos 30 ° + 2021^{0} - \sqrt{12}$ ；

(2)、解分式方程： $\frac{2}{x - 3} = \frac{1}{x - 1}$ .

查看试题解析
20. 先化简，再求值： $[\frac{4}{(\sqrt{x} + \sqrt{y}) (\sqrt{x} - \sqrt{y})} + \frac{\sqrt{x} + \sqrt{y}}{\sqrt{x y} (\sqrt{y} - \sqrt{x})}] \div \frac{\sqrt{x} - \sqrt{y}}{\sqrt{x y}}$ ，其中x＝1，y＝2．

查看试题解析
21. 如图是由边长为1的小正方形构成的 $6 \times 6$ 的网格，点 $A ， B$ 均在格点上.

(1)、在图1中画出以 $A B$ 为对角线的正方形 $A C B D$ ，点 $C ， D$ 为格点.

(2)、在图2中画出以 $A B$ 为边且周长最大的平行四边形 $A B C D$ ，点 $C ， D$ 为格点 (画一个即可).

查看试题解析
22. 操作：第一步：如图1，对折长方形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开.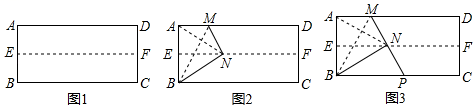
第二步：如图2，再一次折叠纸片，使点A落在EF上的N处，并使折痕经过点B，得到折痕BM，同时得到线段BN.连结AN，易知△ABN的形状是 ▲ .
论证：如图3，若延长MN交BC于点P，试判定△BMP的形状，请说明理由.

查看试题解析
23. 转盘被分成面积相等的若干个扇形，不同扇形分别填涂颜色，分界线可忽略，游戏者同时转动两个转盘，两个转盘停止转动时，若有一个转盘的指针指向红色，另一个转盘的指针指向黄色，则“配橙色”游戏成功，游戏者获胜.求游戏者获胜的概率.（用列表法或画树状图说明）

查看试题解析
24. 如图，等边△ABC中，D，E分别是AB，AC的中点，延长BC到点F，使CF＝ $\frac{1}{2}$ BC，连结DE，CD，EF．

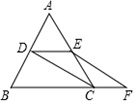(1)、求证：四边形DCFE是平行四边形．

(2)、若AB=6，求四边形DCFE的周长．

查看试题解析
25. 图①是一个长为 $m$ ，宽为 $4 n$ $(m > n)$ 的长方形，用剪刀沿图中虚线剪开，把它平均分成形状和大小都一样的四个小长方形，然后按图②那样拼成一个正方形．

(1)、观察图②，可得： ${(m + n)}^{2} - {(m - n)}^{2} =$ ；

(2)、若 $m - n = 7$ ， $m n = 6$ ，求 ${(m + n)}^{2}$ 的值．

(3)、当 $(x - 10) (20 - x) = 8$ 时，求 ${(2 x - 30)}^{2}$ 的值．

查看试题解析
26. 如图1，在 $⊙ O$ 中， $M$ 为弦 $A B$ 的中点，过点 $M$ 作直径 $C D ， E$ 为线段 $O M$ 上一点，连结 $A E$ 并延长交 $⊙ O$ 于点 $F$ ，连结 $B F$ ， AE=BF.

(1)、证明： $A C = B F$ .

(2)、当 $E M ： O E = 2$ 时，求 $t a n ∠ E A B$ .

(3)、如图2，连结 $C F$ 交 $A B$ 于点 $G$ ，当 $C D = 2$ 时，设 $E M = x ， A G \cdot A B = y$ ，求 $y$ 关于 $x$ 的函数解析式，并确定 $y$ 的最大值.

查看试题解析
27. 如图， $R t △ A B O$ 的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，O为坐标原点，A、B两点的坐标分别为 $(- 3 ， 0)$ 、 $(0 ， 4)$ ，抛物线 $y = \frac{2}{3} x^{2} + b x + c$ 经过B点，且顶点在直线 $x = \frac{5}{2}$ 上.

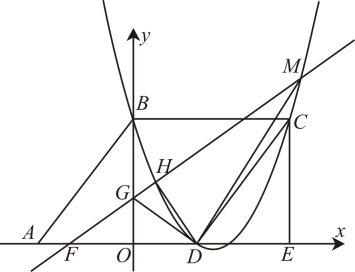(1)、求抛物线对应的函数关系式；

(2)、若 $△ D C E$ 是由 $△ A B O$ 沿x轴向右平移得到的，当四边形ABCD是菱形时，试判断点C和点D是否在该抛物线上，并说明理由；

(3)、在（2）的条件下，若点F与点D关于y轴对称，过点F作直线GF交抛物线于点H、M.点H在点M左侧，连接GD、DM、HD.设直线GF解析式为 $y = k x + b$ ，是否存在实数k，使得 $△ G H D$ 与 $△ D G M$ 相似.若存在，请求出k值以及 $△ D H M$ 的面积，若不存在，请说明理由.

查看试题解析