辽宁省葫芦岛市2022届高三数学第一次模拟考试试卷
试卷更新日期:2022-05-06 类型:高考模拟
一、单选题
-
1. , , 则( )A、 B、{1} C、 D、2. 若复数 , 则( )A、 B、 C、 D、3. 有一组样本数据 , , …, , 由这组数据得到新样本数据, , , …, , 其中 , c为非零常数,则( )A、两组样本数据的样本方差相同 B、两组样本数据的样本众数相同 C、两组样本数据的样本平均数相同 D、两组样本数据的样本中位数相同4. 的展开式中的常数项为( ).A、-120 B、120 C、-60 D、605. 某高中综合实践兴趣小组做一项关于某水果酿制成醋的课题研究.经大量实验和反复论证得出,某水果可以酿成醋的成功指数M与该品种水果中氢离子的浓度N有关,酿醋成功指数M与浓度N满足 . 已知该兴趣小组同学通过数据分析估计出某水果酿醋成功指数为2.9,则该水果中氢离子的浓度约为()( )A、0.2 B、0.4 C、0.6 D、0.86. 函数在单调递增,且为奇函数,若 , 则满足的的取值范围是( )A、 B、 C、 D、7. 已知直线恒过定点M,点N在曲线上,若(O为坐标原点),则的面积为( )A、 B、2 C、 D、8. 已知函数的图象如图所示,将的图象向右平移个单位,使新函数为偶函数,则的最小值为( )
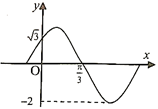 A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
9. 已知抛物线过点 , 焦点为F,则( )A、点M到焦点的距离为3 B、直线MF与x轴垂直 C、直线MF与C交于点N,以弦MN为直径的圆与C的准线相切 D、过点M与C相切的直线方程为10. 对于实数 , , 下列真命题的为( )A、若 , 则 B、若 , , 则 C、若 , 则 D、若 , 且 , 则a+2b的最小值为11. 如图所示,点A,B,C,M,N为正方体的顶点或所在棱的中点,则下列满足平面ABC的是( )A、
 B、
B、 C、
C、 D、
D、 12. 已知函数 , , 函数的图象在点处的切线为 , 与两坐标轴交点分别为 , ;在点的切线为 , 与两坐标轴交点分别为 , . 若两条切线互相垂直,则下列变量范围正确的是( )A、 B、 C、 D、
12. 已知函数 , , 函数的图象在点处的切线为 , 与两坐标轴交点分别为 , ;在点的切线为 , 与两坐标轴交点分别为 , . 若两条切线互相垂直,则下列变量范围正确的是( )A、 B、 C、 D、三、填空题
-
13. 已知向量 , , , . 若 , 则 .14. 写出一个使命题“ , ”成立的充分不必要条件(用m的值或范围作答).15. 已知数列 , , 对于任意正整数m,n,都满足 , 则 .16. 已知双曲线G的方程 , 其左、右焦点分别是 , , 已知点P坐标为 , 双曲线G上点 , 满足 , 则 .
四、解答题
-
17. 记为等差数列的前项和,已知 , .(1)、求的通项公式;(2)、求 , 并求的最大值.18. 如图,四边形ABCD的四个顶点在同一个圆上.已知 , , .
 (1)、求边AB的长;(2)、设 , , 求的值.19. 如图,在正六棱柱中, , .
(1)、求边AB的长;(2)、设 , , 求的值.19. 如图,在正六棱柱中, , . (1)、证明:;(2)、求二面角的正弦值.20. 已知椭圆过点 , , 分别为椭圆C的左、右焦点.请从下面两个条件中选择一个补充到题中,并完成下列问题.条件①:;条件②:离心率 .(1)、求椭圆C的标准方程;(2)、若直线与圆相切,且与椭圆C交于MN两点,求面积的取值范围.21. 葫芦岛市矿产资源丰富,拥有煤、钼、锌、铅等51种矿种,采矿业历史悠久,是葫芦岛市重要产业之一.某选矿场要对即将交付客户的一批200袋钼矿进行品位(即纯度)检验,如检验出品位不达标,则更换为达标产品,检验时;先从这批产品中抽20袋做检验,再根据检验结果决定是否对余下的所有钼矿做检验,设每袋钼矿品位不达标的概率都为 , 且每袋钼矿品位是否达标相互独立.(1)、若20袋钼矿中恰有2袋不达标的概率为 , 求的最大值点;(2)、已知每袋钼矿的检验成本为10元,若品位不达标钼矿不慎出场,对于每袋不达标钼矿要赔付客户110元.现对这批钼矿检验了20袋,结果恰有两袋品位不达标.
(1)、证明:;(2)、求二面角的正弦值.20. 已知椭圆过点 , , 分别为椭圆C的左、右焦点.请从下面两个条件中选择一个补充到题中,并完成下列问题.条件①:;条件②:离心率 .(1)、求椭圆C的标准方程;(2)、若直线与圆相切,且与椭圆C交于MN两点,求面积的取值范围.21. 葫芦岛市矿产资源丰富,拥有煤、钼、锌、铅等51种矿种,采矿业历史悠久,是葫芦岛市重要产业之一.某选矿场要对即将交付客户的一批200袋钼矿进行品位(即纯度)检验,如检验出品位不达标,则更换为达标产品,检验时;先从这批产品中抽20袋做检验,再根据检验结果决定是否对余下的所有钼矿做检验,设每袋钼矿品位不达标的概率都为 , 且每袋钼矿品位是否达标相互独立.(1)、若20袋钼矿中恰有2袋不达标的概率为 , 求的最大值点;(2)、已知每袋钼矿的检验成本为10元,若品位不达标钼矿不慎出场,对于每袋不达标钼矿要赔付客户110元.现对这批钼矿检验了20袋,结果恰有两袋品位不达标.①若剩余钼矿不再做检验,以(1)中确定的作为p的值.这批钼矿的检验成本与赔偿费用的和记作 , 求;
②以①中检验成本与赔偿费用和的期望值为决策依据,是否该对余下的所有钼矿进行检验?
22. 已知函数 , .(1)、求的单调区间;(2)、设 , 若存在 , 使得 , 求证:①;
② .