贵州省普通高等学校招生2022届高三理数全国统一模拟测试试卷
试卷更新日期:2022-05-06 类型:高考模拟
一、单选题
-
1. 设集合 , , 则( )A、{0} B、 C、 D、2. 若复数在复平面内对应的点在直线上,则( )A、-4 B、0 C、2 D、43. 展开式中第5项的系数是( )A、 B、 C、 D、4. 已知命题:函数的最小值为2,命题: , , 则下列命题为真命题的是( )A、 B、 C、 D、5. 生物入侵是指生物由原生存地侵入到另一个新的环境,从而对入侵地的生态系统造成危害的现象.若某入侵物种的个体平均繁殖数量为Q,一年四季均可繁殖,繁殖间隔T为相邻两代间繁殖所需的平均时间.在物种入侵初期,可用对数模型(为常数)来描述该物种累计繁殖数量与入侵时间K(单位:天)之间的对应关系,且 , 在物种入侵初期,基于现有数据得出 , .据此估计该物种累计繁殖数量比初始累计繁殖数量增加11倍所需要的时间为( , )( )A、22.0天 B、13.8天 C、24.8天 D、17.9天6. 已知角 满足 ,则 ( )A、 B、 C、 D、7. 若双曲线的实轴的一个端点是由双曲线的一个焦点和虛轴的两个端点所构成的三角形的重心,则该双曲线的离心率为( )A、3 B、2 C、 D、8. 如图,这是某几何体的三视图,网格纸上小正方形的边长为1,则该几何体的体积为( )
 A、 B、 C、12 D、9. 若是定义在上的偶函数,为奇函数,则( )A、-1 B、0 C、 D、110. 在一个边长为4的正方形的四边上分别取一个距顶点最近的四等分点,连接成正方形,再在新的正方形中,以同样的方式形成一个更小的正方形,如此重复9次,得到如图所示的一个优美图形.若在这个大正方形内部随机投掷一粒豆子,则这粒豆子落在图中阴影部分的概率为( )
A、 B、 C、12 D、9. 若是定义在上的偶函数,为奇函数,则( )A、-1 B、0 C、 D、110. 在一个边长为4的正方形的四边上分别取一个距顶点最近的四等分点,连接成正方形,再在新的正方形中,以同样的方式形成一个更小的正方形,如此重复9次,得到如图所示的一个优美图形.若在这个大正方形内部随机投掷一粒豆子,则这粒豆子落在图中阴影部分的概率为( )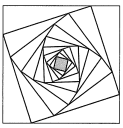 A、 B、 C、 D、11. 如图,已知多面体的底面是边长为的正方形,四边形为等腰梯形,平面平面 , 且 , , 则该几何体外接球的表面积为( )
A、 B、 C、 D、11. 如图,已知多面体的底面是边长为的正方形,四边形为等腰梯形,平面平面 , 且 , , 则该几何体外接球的表面积为( ) A、12π B、16π C、20π D、24π12. 已知函数 , 点是直线与函数的图象从左至右的某三个相邻交点,且 , 则下列命题中正确的是( )
A、12π B、16π C、20π D、24π12. 已知函数 , 点是直线与函数的图象从左至右的某三个相邻交点,且 , 则下列命题中正确的是( )①;②函数在上单调递增;③函数的图象关于直线对称;④将函数的图象向右平移个单位长度后得到的函数图象关于原点对称.
A、①②③ B、②④ C、①③④ D、①④二、填空题
-
13. 函数在处的切线方程为 .14. 已知 , 均为单位向量,且 , 若 , 则.15. 在锐角三角形中,角 , , 所对的边分别为a, , c,已知 , , , 则的面积为.16. 如图,在直角坐标系中,已知椭圆的左、右焦点分别为、 , 点、为椭圆上位于轴上方的两点,且 , 则的取值范围为.

三、解答题
-
17. 2021年9月30日,电影《长津湖》在各大影院.上映,并获得一致好评.该片是以长津湖战役为背景,讲述了一个中国志愿军连队在极度严酷的环境下坚守阵地,奋勇杀敌,为长津湖战役胜利作出重要贡献的感人的历史故事.某同学看完电影后以抗美援朝时期的历史为内容制作了一份知识问卷,并邀请了该校100名同学(男女各一半)参与了问卷的知识竞赛,将得分情况统计如下表:
得分
性别
男生
5
8
13
4
10
5
5
女生
3
10
12
10
6
5
4
将比赛成绩超过60分的考生视为对抗美援朝的历史了解.
附: ,
0.10
0.05
0.010
2.706
3.841
6.635
(1)、从这100名同学中随机抽选一人,求该位同学对抗美援朝的历史了解的频率;(2)、能否有95%的把握认为对抗美援朝的历史了解与性别有关?18. 已知数列的前项和为 , 且 , 数列为等差数列, , .(1)、求数列 , 的通项公式;(2)、数列是由数列的项删去数列的项后按从小到大的顺序排列构成的新数列,求数列的前50项和.19. 如图,在三棱锥中,是边长为4的正三角形, , , 点在底面上的投影为点. (1)、求证:平面平面.(2)、求二面角的余弦值.20. 已知函数(1)、当时,讨论的单调性;(2)、若函数在(为自然对数的底数)上有零点,求实数的取值范围.
(1)、求证:平面平面.(2)、求二面角的余弦值.20. 已知函数(1)、当时,讨论的单调性;(2)、若函数在(为自然对数的底数)上有零点,求实数的取值范围.