广西桂林市、梧州市2022届高三理数高考联合调研（一模）试卷

试卷更新日期：2022-05-05 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知 $R$ 是实数集，集合 $A = {x \in Z | | x | < 3}$ ， $B = {x | 2 x^{2} - x - 3 > 0}$ ，则 $A ∩ (∁_{R} B) =$ （）

A、 ${- 1 ， 0}$ B、 ${- 1 ， 0 ， 1}$ C、 ${0 ， 1 ， 2}$ D、 ${- 1 ， 0 ， 1 ， 2}$

查看试题解析
2. 已知复数 $z = (a - 2 i) (1 + 3 i) (a \in R)$ 的实部与虚部的和为12，则 $| z - 5 | =$ （）

A、3 B、4 C、5 D、6

查看试题解析
3. 已知向量 $\vec{a} = (1 ， - \sqrt{7})$ ， $| \vec{b} | = 3$ ， $\vec{a} \cdot \vec{b} = 3 \sqrt{6}$ ，则 $\vec{a}$ 与 $\vec{b}$ 的夹角为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{4}$ C、 $\frac{π}{3}$ D、 $\frac{2 π}{3}$

查看试题解析
4. 北京天坛圜丘坛的地面由石板铺成，最中间的是圆形的天心石，围绕天心石的是9圈扇环形的石板，从内到外各圈的石板数依次为 $a_{1} ， a_{2} ， a_{3} ， \cdot \cdot \cdot ， a_{9}$ ，设数列 ${a_{n}}$ 为等差数列，它的前 $n$ 项和为 $S_{n}$ ，且 $a_{2} = 18$ ， $a_{4} + a_{6} = 90$ ，则 $S_{8} =$ （）

A、189 B、252 C、324 D、405

查看试题解析
5. 已知 $M$ 为抛物线 $C ：$ $x^{2} = 2 p y (p > 0)$ 上一点，点 $M$ 到 $C$ 的焦点的距离为7，到 $x$ 轴的距离为5，则 $p =$ （）

A、3 B、4 C、5 D、6

查看试题解析
6. 已知 $t a n α = 2$ ，则 $\frac{c o s^{3} α - c o s α}{c o s (α + \frac{π}{2})} =$ （）

A、 $\frac{2}{5}$ B、 $\frac{3}{4}$ C、 $\frac{2}{3}$ D、 $\frac{1}{2}$

查看试题解析
7. 某几何体的三视图如图所示，则该几何体的体积是（）

A、18 B、36 C、54 D、108

查看试题解析
8. 某保险公司销售某种保险产品，根据2020年全年该产品的销售额（单位：万元）和该产品的销售额占总销售额的百分比，绘制出如图所示的双层饼图.根据双层饼图，下列说法正确的是（）

A、2020年第四季度的销售额为380万元 B、2020年上半年的总销售额为500万元 C、2020年2月份的销售额为60万元 D、2020年12个月的月销售额的众数为60万元

查看试题解析
9. 第24届冬季奥运会将于2022年2月4日至2022年2月20日在北京市和河北省张家口市举行．现要安排甲、乙、丙、丁四名志愿者去国家高山滑雪馆、国家速滑馆、首钢滑雪大跳台三个场馆参加活动，要求每个场馆都有人去，且这四人都在这三个场馆，则甲和乙都没被安排去首钢滑雪大跳台的种数为（）

A、12 B、14 C、16 D、18

查看试题解析
10. 在四边形 $A B C D$ 中（如图1所示）， $A B = A D$ ， $∠ A B D = 4 5^{∘}$ ， $B C = B D = C D = 2$ ，将四边形 $A B C D$ 沿对角线 $B D$ 折成四面体 $A^{'} B C D$ （如图2所示），使得 $∠ A^{'} B C = 9 0^{∘}$ ， E，F，G分别为棱 $B C$ ， $A^{'} D$ ， $A^{'} B$ 的中点，连接 $E F$ ， $C G$ ，则下列结论错误的是（）．

A、 $A^{'} C ⊥ B D$ B、直线 $E F$ 与 $C G$ 所成角的余弦值为 $\frac{4 \sqrt{5}}{15}$ C、C，E，F，G四点不共面 D、四面体 $A^{'} B C D$ 外接球的表面积为 $8 π$

查看试题解析
11. 已知双曲线 $C$ ： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点分别为 $F_{1} ， F_{2}$ ，左、右顶点分别为 $A_{1} ， A_{2}$ ， $P$ 为双曲线的左支上一点，且直线 $P A_{1}$ 与 $P A_{2}$ 的斜率之积等于3，则下列说法正确的是（）

A、双曲线 $C$ 的离心率为 $\sqrt{3}$ B、若 $P F_{1} ⊥ P F_{2}$ ，且 $S_{△ P F_{1} F_{2}} = 3$ ，则 $a = 2$ C、以线段 $P F_{1}$ ， $A_{1} A_{2}$ 为直径的两个圆外切 D、若点 $F_{2}$ 到 $C$ 的一条渐近线的距离为 $\sqrt{3}$ ，则 $C$ 的实轴长为4

查看试题解析
12. 已知 $i \in N^{*}$ ，数列1，1，2，1，1，2，4，2，1，1，2，4，8，4，2，1，···，1，2，4，···， $2^{i}$ ， $2^{i - 1}$ ， ···，2，1，···的前 $n$ 项和为 $S_{n}$ ，若 $S_{n} > 2022$ ，则 $n$ 的最小值为（）

A、81 B、90 C、100 D、2021

查看试题解析

二、填空题

13. 已知 $f (x)$ 是奇函数，且当 $x > 0$ 时， $f (x) = - l n (a x)$ ．若 $f (- e^{2}) = 2$ ，则 $a =$ ．

查看试题解析
14. 若 $x$ ， $y$ 满足约束条件 ${\begin{array}{l} y ⩾ - 1 ， \\ 3 x + y - 5 ⩽ 0 ， \\ 3 x - 2 y + 1 ⩾ 0 ， \end{array}$ 则 $z = x + y$ 的最大值为．

查看试题解析
15. 若曲线 $y = l n x$ 在点 $P (e ， 1)$ 处的切线与曲线 $y = e^{a x}$ 相切，则 $a =$ ．

查看试题解析
16. 函数 $f (x) = 2 s i n (ω x + φ) (ω > 0 ， 0 < φ < π)$ 的部分图象如图所示，其中 $f (0) = f (\frac{5 π}{9})$ ， $f (- \frac{2 π}{9}) = 0$ ，若对于任意的 $x_{1} \in [- \frac{π}{9} ， \frac{π}{6})$ ， $x_{2} \in (\frac{π}{6} ， \frac{π}{3})$ ， $f (x_{1}) - λ > c o s 2 x_{2} - s i n 3 x_{1}$ 恒成立，则实数 $λ$ 的取值范围为．

查看试题解析

三、解答题

17. 在 $△ A B C$ 中，内角A，B，C所对的边分别为a，b，c， $△ A B C$ 的面积为S，已知 $a c o s C + c c o s A = \sqrt{3}$ ， $a = \sqrt{2} b$ ．

(1)、求a；

(2)、若 $S = \frac{\sqrt{3}}{12} (a^{2} + c^{2} - b^{2})$ ，求A．

查看试题解析
18. 某中学组织一支“雏鹰”志愿者服务队，带领同学们利用周末的时间深入居民小区开展一些社会公益活动．现从参加了环境保护和社会援助这两项社会公益活动的志愿者中，随机抽取男生80人，女生120人进行问卷调查（假设每人只参加环境保护和社会援助中的一项），整理数据后得到如下统计表：

女生
男生
合计
环境保护
80
40
120
社会援助
40
40
80
合计
120
80
200
附： $K^{2} = \frac{n (a d - b c)^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ ．
$P (K^{2} \geq k_{0})$
0.025
0.010
0.005
0.001
$k_{0}$
5.024
6.635
7.879
10.828

(1)、能否有99％的把握认为学生参加社会公益活动所选取的项目与学生性别有关？

(2)、以样本的频率作为总体的概率，若从本校所有参加社会公益活动的女生中随机抽取4人，记这4人中参加环境保护的人数为 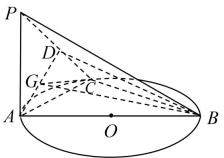$X$ ，求 $X$ 的分布列和期望．

查看试题解析
19. 如图， $A B$ 是圆 $O$ 的直径， $P A ⊥$ 圆 $O$ 所在的平面， $C$ 为圆周上一点， $D$ 为线段 $P C$ 的中点， $∠ C B A = 3 0^{°}$ ， $A B = 2 P A$ ．

(1)、证明：平面 $A B D ⊥$ 平面 $P B C$ .

(2)、若 $G$ 为 $A D$ 的中点，求二面角 $P - B C - G$ 的余弦值.

查看试题解析
20. 已知O坐标原点，椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的上顶点为A，右顶点为B， $△ A O B$ 的面积为 $\frac{\sqrt{2}}{2}$ ，原点O到直线AB的距离为 $\frac{\sqrt{6}}{3}$ ．

(1)、求椭圆C的方程；

(2)、过C的左焦点F作弦DE，MN，这两条弦的中点分别为P，Q，若 $\vec{D E} \cdot \vec{M N} = 0$ ，求 $△ F P Q$ 面积的最大值．

查看试题解析
21. 已知函数 $f (x) = l n x + 2$ ， $g (x) = \frac{1}{a} e^{2 x} - l n \frac{2}{a} (a > 0)$ ．

(1)、设函数 $h (x) = f (x + 1) - x - 2$ ，求 $h (x)$ 的最大值；

(2)、证明： $f (x) \leq g (x)$ ．

查看试题解析
22. 在直角坐标系 $x O y$ 中，直线 $l$ 的参数方程为 ${\begin{array}{l} x = 4 - \frac{\sqrt{3}}{2} t ， \\ y = 2 + \frac{1}{2} t \end{array}$ （ $t$ 为参数）．以坐标原点 $O$ 为极点， $x$ 轴的非负半轴为极轴建立极坐标系，圆 $C$ 的极坐标方程为 $ρ^{2} - 2 ρ c o s θ - 4 ρ s i n θ - 1 = 0$ ．

(1)、求圆 $C$ 的直角坐标方程；

(2)、设圆 $C$ 与直线 $l$ 交于点 $A$ ， $B$ ，若点 $P$ 的坐标为（4，2），求 $| P A | + | P B |$ ．

查看试题解析
23. 已知函数 $f (x) = | 2 x - \frac{1}{a} | + | 2 x + a | (a > 0)$ ．

(1)、当 $a = 1$ 时，求不等式 $f (x) \leq 3$ 的解集；

(2)、若 $f (\frac{3}{2}) < 6$ ，求 $a$ 的取值范围．

查看试题解析

	女生	男生	合计
环境保护	80	40	120
社会援助	40	40	80
合计	120	80	200

$P (K^{2} \geq k_{0})$	0.025	0.010	0.005	0.001
$k_{0}$	5.024	6.635	7.879	10.828