广东省惠州市2022届高三下学期数学一模试卷

试卷更新日期：2022-05-05 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $M = {- 2 ， 1 ， 2 ， 3}$ ， $N = {- 2 ， 2}$ ，下列结论成立的是（）

A、 $M \subseteq N$ B、 $M \cap N = \emptyset$ C、 $M ∪ N = M$ D、 $∁_{M} N = {1}$

查看试题解析
2. 若抛物线 $y^{2} = 2 p x$ （ $p > 0$ ）上一点P（2， $y_{0}$ ）到其焦点的距离为4，则抛物线的标准方程为（）

A、y²=2x B、y²=4x C、y²=6x D、y²=8x

查看试题解析
3. 已知 $t a n α = 2$ ， $π < α < \frac{3}{2} π$ ，则 $c o s α - s i n α =$ （）

A、 $\frac{\sqrt{5}}{5}$ B、 $- \frac{\sqrt{5}}{5}$ C、 $\frac{3 \sqrt{5}}{5}$ D、 $- \frac{3 \sqrt{5}}{5}$

查看试题解析
4. 若 ${(1 - 2 x)}^{2022} = a_{0} + a_{1} x + a_{2} x^{2} + \cdot \cdot \cdot + a_{2022} x^{2022}$ ，则 $a_{1} + a_{2} + \cdot \cdot \cdot + a_{2022} =$ （）

A、-1 B、0 C、1 D、2

查看试题解析
5. 现有 $3$ 名学生报名参加校园文化活动的3个项目，每人须报1项且只报1项，则恰有2名学生报同一项目的报名方法有（）

A、36种 B、18种 C、9种 D、6种

查看试题解析
6. 已知 $f (x) = {\begin{array}{l} e^{x - 4} ， x \leq 4 \\ (x - 16)^{2} - 143 ， x > 4 \end{array}$ ，则当 $x \geq 0$ 时， $f (2^{x})$ 与 $f (x^{2})$ 的大小关系是（）

A、 $f (2^{x}) \leq f (x^{2})$ B、 $f (2^{x}) \geq f (x^{2})$ C、 $f (2^{x}) = f (x^{2})$ D、不确定

查看试题解析
7. 设等差数列 ${a_{n}}$ 的公差为d，若 $b_{n} = 2^{a_{n}}$ ，则“ $d < 0$ ”是“ $b_{n + 1} < b_{n}$ （ $n \in N^{*}$ ）”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
8. 中国的5G技术领先世界，5G技术的数学原理之一便是著名的香农公式： $C = W l o g_{2} (1 + \frac{S}{N})$ ，它表示：在受噪声干扰的信道中，最大信息传递速率C取决于信道带宽W､信道内信号的平均功率S､信道内部的高斯噪声功率N的大小，其中 $\frac{S}{N}$ 叫做信噪比.当信噪比比较大时，公式中真数中的1可以忽略不计，按照香农公式，若不改变带宽W，而将信噪比 $\frac{S}{N}$ 从1000提升至5000，则C大约增加了（）（附： $l g 2 \approx 0.3010$ ）

A、20% B、23% C、28% D、50%

查看试题解析

二、多选题

9. 对于实数 $a ， b ， c$ ，下列结论正确的是（）

A、若 $a > b$ ，则 $a c < b c$ B、若 $a c^{2} > b c^{2}$ ，则 $a > b$ C、若 $a < b < 0$ ，则 $| a | > | b |$ D、若 $c > a > b > 0$ ，则 $\frac{1}{c - a} > \frac{1}{c - b}$

查看试题解析
10. 如图，点O是正八边形ABCDEFGH的中心，且 $| \vec{A B} | = 1$ ，则（）

A、 $\vec{A H}$ 与 $\vec{C F}$ 能构成一组基底 B、 $\vec{O A} \cdot \vec{O C} = 0$ C、 $\vec{O A} + \vec{O C} = \sqrt{2} \vec{O B}$ D、 $\vec{A C} \cdot \vec{C D} = - \frac{\sqrt{2}}{2}$

查看试题解析
11. 已知函数 $f (x) = A s i n (ω x + φ)$ （其中 $A > 0$ ， $ω > 0$ ， $| φ | < π$ ）的部分图象如图所示，则下列结论正确的是（）

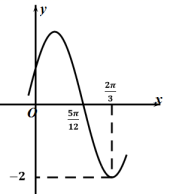A、函数 $f (x)$ 的图象关于 $x = \frac{π}{2}$ 直线对称 B、函数 $f (x)$ 的图象关于点 $(- \frac{π}{12} ， 0)$ 对称 C、函数 $f (x)$ 在区间 $[- \frac{π}{3} ， \frac{π}{6}]$ 上单调递增 D、 $y = 1$ 与图象 $y = f (x) (- \frac{π}{12} \leq x \leq \frac{23 π}{12})$ 的所有交点的横坐标之和为 $\frac{8 π}{3}$

查看试题解析
12. 近年来，纳米晶的多项技术和方法在水软化领域均有重要应用.纳米晶体结构众多，下图是一种纳米晶的结构示意图，其是由正四面体沿棱的三等分点作平行于底面的截面得到所有棱长均为n的几何体，则下列说法正确的有（）

A、该结构的纳米晶个体的表面积为 $7 \sqrt{3} n^{2}$ B、该结构的纳米晶个体的体积为 $\frac{23 \sqrt{2}}{12} n^{3}$ C、该结构的纳米晶个体外接球的表面积为 $\frac{11}{4} π n^{2}$ D、二面角A₁−A₂A₃−B₃的余弦值为 $- \frac{1}{3}$

查看试题解析

三、填空题

13. 已知i是虚数单位，则复数 ${(\frac{1 + i}{\sqrt{2}})}^{4}$ 的模等于.

查看试题解析
14. 已知双曲线 $C$ 的渐近线方程为 $y = \pm \frac{\sqrt{2}}{2} x$ ，则双曲线 $C$ 的标准方程可以是.（写出一个正确的方程即可.）

查看试题解析
15. 若一个圆台的侧面展开图是半圆面所在的扇环，且扇环的面积为 $4 π$ ，圆台上､下底面圆的半径分别为 $r_{1}$ ， $r_{2}$ （ $r_{1} < r_{2}$ ），则 $r_{2}^{2} - r_{1}^{2} =$ .

查看试题解析
16. 如图，曲柄连杆机构中，曲柄CB绕C点旋转时，通过连杆AB的传递，活塞做直线往复运动.当曲柄在CB₀位置时，曲柄和连杆成一条直线，连杆的端点A在A₀处.设连杆AB长200 $m m$ ，曲柄CB长70 $m m$ ，则曲柄自CB₀按顺时针方向旋转53.2°时，活塞移动的距离（即连杆的端点A移动的距离A₀A）约为 $m m$ .（结果保留整数）（参考数据：sin53.2°≈0.8）

查看试题解析

四、解答题

17. 惠州市某高中学校组织航天科普知识竞赛，分小组进行知识问题竞答.甲乙两个小组分别从6个问题中随机抽取3个问题进行回答，答对题目多者为胜.已知这6个问题中，甲组能正确回答其中4个问题，而乙组能正确回答每个问题的概率均为 $\frac{2}{3}$ .甲､乙两个小组的选题以及对每题的回答都是相互独立，互不影响的.

(1)、求甲小组至少答对2个问题的概率；

(2)、若从甲乙两个小组中选拔一组代表学校参加全市决赛，请分析说明选择哪个小组更好？

查看试题解析
18. 在△ABC中，内角A，B，C所对的边分别为a，b，c， $1 - c o s 2 B = c o s (A - C) + c o s B$ ，且 $\vec{A D} = \vec{D C}$ .

(1)、求证： $b^{2} = a c$ ；

(2)、当 $B D = b$ 时，求 $c o s ∠ A B C$ .

查看试题解析
19. 已知数列 ${a_{n}} ， {b_{n}}$ 满足 $b_{n} = a_{n} - (- 1)^{n} n^{2} ， a_{1} + b_{1} = 1 ， a_{2} + b_{2} = 8$ ，且数列 ${b_{n}}$ 是等差数列.

(1)、求数列 ${a_{n}}$ 的通项公式：

(2)、设数列 ${a_{n}}$ 的前 $n$ 项和为 $T_{n}$ ，若 $A = {n ∣ n \leq 110$ 且 $T_{n} \leq 110}$ ，求集合A中所有元素的和T.

查看试题解析
20. 如图1所示，梯形ABCD中，AB=BC=CD=2，AD=4，E为AD的中点，连结BE，AC交于F，将△ABE沿BE折叠，使得平面ABE⊥平面BCDE（如图2）.

(1)、求证：AF⊥CD；

(2)、求平面AFC与平面ADE的夹角的余弦值.

查看试题解析
21. 已知抛物线C₁： $y^{2} = 4 x$ 与椭圆C₂： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （ $a > b > 0$ ）有公共的焦点，C₂的左､右焦点分别为F₁ ， F₂ ，该椭圆的离心率为 $\frac{1}{2}$ .

(1)、求椭圆C₂的方程；

(2)、如图，若直线l与x轴，椭圆C₂顺次交于P，Q，R（P点在椭圆左顶点的左侧），且∠PF₁Q与∠PF₁R互为补角，求△F₁QR面积S的最大值.

查看试题解析
22. 已知函数 $f (x) = e^{x} + m s i n x - \frac{1}{2} x^{2} - 1$ （ $m \in R$ ）.

(1)、当m=0时，讨论 $f (x)$ 的单调性；

(2)、若不等式 $x \cdot f (x) \geq 0$ 对 $x \in [- \frac{π}{2} ， \frac{π}{2}]$ 恒成立，求m的取值范围.

查看试题解析