2021-2022苏科版数学七年级下册10.4 三元一次方程组同步练习

试卷更新日期：2022-05-02 类型：同步测试

进入出卷网下载

一、单选题

1. 三元一次方程组 ${\begin{cases} 2 x - 3 y + 4 z = 3 \\ 3 x - 2 y + z = 7 \\ x + 2 y - 3 z = 1 \end{cases}$ 的解为（）

A、 B、 C、 D、

查看试题解析
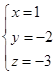2. 已知三元一次方程组 ${\begin{matrix} x + y = 10 \\ y + z = 20 \\ z + x = 40 \end{matrix}$ ，则x+y+z=（）

A、20 B、30 C、35 D、70

查看试题解析
3. 已知 ${\begin{cases} x = 1 \\ y = 2 \\ z = 3 \end{cases}$ 是方程组 ${\begin{cases} a x + b y = 2 \\ b y + c z = 3 \\ c x + a z = 7 \end{cases}$ 的解，则a+b+c的值是（）

A、3 B、2 C、1 D、无法确定

查看试题解析
4.
以为解建立三元一次方程组，不正确的是（）

A、 $3 x - 4 y + 2 z = 3$ B、 C、 $x + y - z = - 2$ D、 $\frac{x}{2} - \frac{2}{3} y - z = 1 \frac{5}{6}$

查看试题解析
5. 若三元一次方程组 ${\begin{matrix} x + y = 5 \\ x + z = - 1 \\ y + z = - 2 \end{matrix}$ 的解使ax+2y+z=0，则a的值为（）

A、1 B、0 C、﹣2 D、4

查看试题解析
6. 设“●■▲”分别表示三种不同的物体，如图所示，前两架天平保持平衡，如果要使第三架天平也平衡，那么“？”处应放“■”的个数为（）

A、5 B、4 C、3 D、2

查看试题解析
7. 已知方程组 ${\begin{array}{l} x - y = 5 \\ 4 x - 3 y + k = 0 \end{array}$ 的解也是方程3x－2y=0的解，则k的值是（）

A、k=－5 B、k=5 C、k=－10 D、k=10

查看试题解析

二、填空题

8. 已知 ${\begin{matrix} x + y = 5 \\ y + z = - 2 \\ z + x = 3 \end{matrix}$ ，则x＋y＋z＝.

查看试题解析
9. 有甲、乙、丙三种货物，若购买甲2件、乙8件、丙5件共需400元；若购买甲3件、乙11件、丙7件只需600元，则购买甲、乙、丙各一件共需元.

查看试题解析
10. 已知a、b、c满足 ${\begin{cases} 4 a - 2 b + c = 0 \\ a + b + c = 0 \\ 4 a + 2 b + c = 8 \end{cases}$ ，则a= ， b= ， c= ．

查看试题解析
11. 判断 ${\begin{cases} x = 5 \\ y = 10 \\ z = - 15 \end{cases}$ 是否是三元一次方程组 ${\begin{cases} x + y + z = 0 \\ 2 x - y + z = - 15 \\ x + 2 y - z = 40 \end{cases}$ 的解：（填：“是”或者“不是”）．

查看试题解析
12. 已知 ${\begin{matrix} 4 x -3 y -6 z = 0, \\ 2 x + 4 y -14 z = 0 \end{matrix}$ (x,y,z≠0),则 $\frac{2 x^{2} + 3 y^{2} + 6 z^{2}}{x^{2} + 5 y^{2} + 7 z^{2}}$ 的值为.

查看试题解析
13. 解三元一次方程组 ${\begin{matrix} 3 x + 2 y + z = 13 ① \\ x + y + 2 z = 7 ② \\ 2 x + 3 y - z = 12 ③ \end{matrix}$ 时，首先消去z，得二元一次方程组为，再消去未知数x，得一元一次方程为.解得y=；将y代入变形得到的二元一次方程组中，求得x= ，最后将x和y值同时代入②；得z=.

查看试题解析
14. “洞庭碧螺春，品香醉天下.”洞庭碧螺春产于苏州市太湖洞庭山，以形美、色艳、香浓、味醇“四绝”驰名中外.如图，若将一壶碧螺春茶倒满2个小杯，则还剩 $\frac{1}{4}$ 壶；若倒满1个小杯后再全部倒入1个大杯中，则只能倒满这个大杯的 $\frac{1}{2}$ .1个小杯与1个大杯的容积之比为.

查看试题解析

三、计算题

15. 解下列方程组或不等式（组）：

(1)、 ${\begin{array}{l} 3 x + 5 y = 8 \\ 2 x - y = 1 \end{array}$

(2)、 ${\begin{array}{l} x + y + z = 1 \\ x - 2 y - z = 3 \\ 2 x - y + z = 0 \end{array}$

查看试题解析
16. 解下列方程组：

(1)、 ${\begin{array}{l} y - x = - 3 \\ 7 x - 5 y = 9 \end{array}$ （代入法）；

(2)、 ${\begin{matrix} 2 x + y = 5 \\ 3 x - 2 y = 11 \end{matrix}$ （加减法）；

(3)、 ${\begin{matrix} \frac{a}{3} = \frac{b}{4} = \frac{c}{5} \\ 2 a - 3 b + c = 6 \end{matrix}$ .

查看试题解析
17. 已知关于 $x$ ， $y$ 的二元一次方程组 ${\begin{matrix} 3 x + 4 y = k \\ x + 2 y = - 1 \end{matrix}$ 的解互为相反数，求k的值.

查看试题解析

四、解答题

18. 小明去超市买三种商品．其中丙商品单价最高．如果购买3件甲商品、2件乙商品和1件丙商品，那么需要付费20元，如果购买4件甲商品，3件乙商品和2件丙商品，那么需要付费32元．
（1）如果购买三种商品各1件，那么需要付费多少元？
（2）如果需要购买1件甲商品，3件乙商品和2件丙商品，那么小明至少需多少钱才能保证一定能全部买到？（结果精确到元）

查看试题解析
19. 对于未知数为 $x$ ， $y$ 的二元一次方程组，如果方程组的解 $x$ ， $y$ 满足 $| x - y | = 1$ ，我们就说方程组的解 $x$ 与 $y$ 具有“邻好关系”.

(1)、方程组 ${\begin{matrix} x + 2 y = 7 \\ x = y + 1 \end{matrix}$ 的解 $x$ 与 $y$ 是否具有“邻好关系”?说明你的理由：

(2)、若方程组 ${\begin{matrix} 4 x - y = 6 \\ 2 x + y = 4 m \end{matrix}$ 的解 $x$ 与 $y$ 具有“邻好关系”，求 $m$ 的值：

(3)、未知数为 $x$ ， $y$ 的方程组 ${\begin{array}{l} x + a y = 7 \\ 2 y - x = 5 \end{array}$ ，其中 $a$ 与 $x$ 、 $y$ 都是正整数，该方程组的解 $x$ 与 $y$ 是否具有“邻好关系”?如果具有，请求出 $a$ 的值及方程组的解：如果不具有，请说明理由.

查看试题解析
20. （阅读感悟）
对于方程组的问题，有时候要求的结果不是每个未知数的值，而是求关于未知数的代数式的值.如已知实数 $a$ 、 $b$ 满足 ${\begin{array}{l} 3 a - b = 5 ① \\ 2 a + 3 b = 7 ② \end{array}$ ，求 $a - 4 b$ 和 $7 a + 5 b$ 的值.

方法一：解方程组，分别求出 $a$ 、 $b$ 的值，代入代数式求值；

方法二：仔细观察两个方程中未知数的系数之间的关系，通过适当变形整体求代数式的值.解法如下：

①－②，得： $a - 4 b = - 2$ ；①＋②×2，得： $7 a + 5 b = 19$ .

比较：方法一运算量较大，是常规思路；方法二运算较为简单，这种解题思路就是通常所说的“整体思想”.

（问题解决）

(1)、已知二元一次方程组 ${\begin{array}{l} 3 x + 2 y = 7 \\ 2 x + 3 y = 5 \end{array}$ ，则 $x - y =$ ； $x + y =$ .

(2)、某班级因组织活动购买奖品.买13支铅笔、4块橡皮、2本笔记本共需48元；买25支铅笔、7块橡皮、3本笔记本共需84元.则购买5只铅笔、5块橡皮、5本笔记本共需元.

(3)、对于实数 $x$ 、 $y$ ，定义新运算： $x ※ y = a x + b y - c$ ，其中 $a$ 、 $b$ 、 $c$ 是常数，等式右边是通常的加减法和乘法运算.已知 $3 ※ 5 = 15$ ， $4 ※ 7 = 28$ ，那么 $1 ※ 1$ 的值是.

查看试题解析