山西省太原市2021-2022学年高一下学期物理期中质量监测试卷

试卷更新日期：2022-04-29 类型：期中考试

进入出卷网下载

一、单选题

1. 关于物体的受力和运动，下列说法中正确的是（）

A、物体做曲线运动时，其速度可能不变 B、物体做曲线运动时，某点加速度的方向沿这一点曲线的切线方向 C、物体受到变化的合力作用时，它的速度大小一定改变 D、物体的运动状态改变时，其运动轨迹可能是直线，也可能是曲线

查看试题解析
2. 对于生活中的离心运动，下列说法正确的是（）

A、增大洗衣机脱水筒转动的周期可以使衣服甩的更干 B、汽车转弯时，若转弯半径过大会引起侧滑而造成交通事故 C、赛跑通过弯道时，身体应该向弯道内侧倾斜一些 D、当火车速度低于规定速度通过弯道时，轮缘会对外轨产生挤压

查看试题解析
3. 一颗卫星在地球表面所受的重力大小为G，当它被发射到距地球表面高度为6倍地球半径的轨道上时，所受地球对它的万有引力大小为（）

A、 $\frac{G}{6}$ B、 $\frac{G}{7}$ C、 $\frac{G}{36}$ D、 $\frac{G}{49}$

查看试题解析
4. 在建立万有引力定律的过程中，下面说法错误的是（）

A、建构了模型，将椭圆轨道简化为圆轨道 B、使用了卡文迪许得到的引力常量 C、运用牛顿第三定律进行了推理 D、用“月-地检验”进行了验证

查看试题解析
5. 用挖掘机从底部拆除高大的烟囱，在烟囱即将倒下时，司机会紧盯烟囱的顶端，根据顶端的运动情形判断烟囱倒下的方向，从而针对性回避。以下说法正确的是（）

A、烟囱倒下时，其顶端的线速度较大，易于判断 B、烟囱倒下时，其顶端的角速度较大，易于判断 C、烟囱倒下时，其顶端的向心加速度较小，易于判断 D、烟囱倾倒的方向与顶端的速度方向无关

查看试题解析
6. 太原方特中的《勇闯鹿族》过山车，既有在轨道外侧的圆周运动，也有在轨道内侧的圆周运动，如图甲、乙所示。过山车都有安全锁（由上、下、侧三个轮子组成），把过山车套在了轨道上，设两图中轨道的半径都为R，下列说法正确的是（）

A、甲图中，过山车通过轨道最高点时，对人的作用力一定向上 B、乙图中，过山车通过轨道最低点时，对人的作用力一定向上 C、甲图中，过山车通过轨道最高点时的最小速度为 $\sqrt{g R}$ D、乙图中，过山车通过轨道最低点时，对人的作用力可能小于他的重力

查看试题解析
7. 2月15日，中国小将苏翊鸣在北京冬奥会摘得了男子单板滑雪金牌。如图是他在空中翻转时经多次连续曝光得到的照片，相邻两次曝光的时间间隔相等。已知他重心的轨迹与同速度斜抛小球（不计空气阻力）的轨迹重合，A、B、C和D表示其重心的位置，且A和D处于同一高度。将运动员视为质量集中于重心的质点，则运动员（）

A、在A，D位置时的速度相同 B、从A到B和从C到D的时间相同 C、相邻时间间隔内速度的变化相同 D、运动最高点位于B和C中间

查看试题解析
8. 一个可以看作质点的小球从y轴上的A点开始做平抛运动，经过时间t到达P点，最后落到x轴上的Q点。已知P点的横坐标和纵坐标相等，小球经过P点时速度方向与x轴正方向成45°角，则小球从A点运动到Q点的时间为（）

A、 $\sqrt{2} t$ B、 $\sqrt{3} t$ C、 $\frac{\sqrt{2}}{2} t$ D、 $\frac{\sqrt{3}}{2} t$

查看试题解析
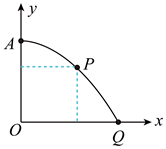9. 往复式活塞压缩机原理如图所示，圆盘上的B点与活塞上的A点通过铰链连接在直杆两端，圆盘绕固定转动轴O点以角速度ω逆时针匀速转动，从而使活塞水平左右移动。以O为圆心，AO为x正方向建立如图的坐标系，已知 $O B = R$ ，下列说法正确的是（）

A、当B到达（R，0）位置时，活塞的速度最大 B、当B到达（0，R）位置时，活塞的速度向左且最大 C、在B从（0，R）到（-R，0）的过程中，活塞的速度先增大后减小 D、在B从（0，R）到（0，-R）的过程中，活塞的速度先增大后减小

查看试题解析
10. 如图，两个完全相同的小球P、Q被细绳 $O P$ 、 $O Q$ 悬挂在同一点O，并在同一水平面内做匀速圆周运动，且绳长度 $O P = 2 O Q$ ，则（）

A、 $O P$ 绳张力的值等于 $O Q$ 绳张力的值的2倍 B、P球角速度的值等于Q球角速度的值的2倍 C、P球向心加速度的值等于Q球向心加速度的值 D、P球线速度的值等于Q球线速度的值的2倍

查看试题解析

二、多选题

11. 百武彗星是人类第一次探测到发射X射线的彗星，它的近日点仅0.1AU，周期很长（200年以上）。已知地球的轨道半径为1AU，只考虑行星与太阳间的作用力，下列说法正确的是（）

A、百武彗星在近日点的速度比在远日点的速度大 B、百武彗星轨道的半长轴大于地球的轨道半径 C、太阳处在百武彗星椭圆轨道的中心点上 D、在远离太阳的过程中，百武彗星与太阳的连线在相等时间内扫过的面积逐渐增大

查看试题解析
12. 图甲是一种可自动计数的智能呼啦圈。腰带外侧带有轨道，将带有滑轮的短杆穿入轨道，短杆的另一端固定有配重，其简化模型如图乙所示。锻炼身体时，水平固定好腰带，通过人体微小扭动，这时腰带可看作不动，配重可视为在水平面内做匀速圆周运动，下列说法正确的是（）

A、匀速转动时，配重受到的合力恒定不变 B、若增大转速，腰受到腰带的弹力变大 C、若增大转速，杆受到配重的弹力变大 D、如果转速足够大，配重可上升到腰带所在的高度

查看试题解析
13. 河流中河水的速度大小为5m/s，小船相对于静水的速度大小为3m/s。小船船头正对河岸渡河时，恰好行驶到河对岸的B点。若小船船头偏向上游某方向渡河，则小船（）

A、到达对岸时一定在B点的上游 B、到达对岸时可能还在B点 C、渡河时间可能变短 D、渡河位移可能变短

查看试题解析
14. 汽车更换轮胎后其重心会偏离转轴，这时需对轮胎进行动平衡旋转（动平衡）调整。卸下轮胎固定在动平衡机上，在轮毂上的恰当位置贴上适当质量的平衡块，就可以让其重心恢复到转轴。若平衡块的质量为m，与转轴的距离为R，当轮胎以角速度 $ω$ 匀角速转动时（）

A、若平衡块到达最高点时车轴受到的合力竖直向上，则应减小平衡块的质量 B、若平衡块到达最高点时车轴受到的合力沿水平方向，则只应调整平衡块的质量 C、平衡块到达最低点时对轮毂的作用力大小为 $m ω^{2} R$ D、平衡块到达与转轴等高的位置时，受到轮毂的作用力为 $m \sqrt{ω^{4} R^{2} + g^{2}}$

查看试题解析
15. 在斜面的顶端，将甲、乙两小球分别以v和 $\frac{v}{2}$ 的速度沿同一方向水平抛出，两球都落在该斜面上。则（）

A、甲、乙两球的水平位移之比为2∶1 B、甲、乙两球的水平位移之比为4∶1 C、甲、乙两球落至斜面时的速率之比为4∶1 D、甲、乙两球落至斜面时的速率之比为2∶1

查看试题解析

三、实验题

16. 如图，向心力演示器塔轮自上而下有三层，对应各层左、右半径之比分别是1∶1、2∶1和3∶1，A、C到左、右塔轮中心的距离相等，A、B的距离等于A到左塔轮中心的距离。实验时转动手柄，塔轮、长槽和短槽随之转动。

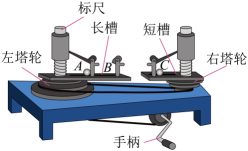(1)、在探究向心力与半径、质量、角速度的关系时，用到的实验方法是____。

A、理想实验 B、等效替代法 C、微元法 D、控制变量法

(2)、保持两小球质量相等，将小球分别放在B处和C处，同时左、右塔轮采用1∶1半径比，可得到的关系是；将小球分别放在A处和C处，同时左、右塔轮采用2∶1半径比，可得到的关系是；（填正确选项字母）
A．质量和角速度一定时，向心力的大小与半径的关系
B．质量和半径一定时，向心力的大小与角速度的关系

(3)、在探究角速度和半径一定的条件下向心力与小球质量的关系时，应将质量不同的两小球分别放在处（选填“A和B”、“A和C”或“B和C”），同时左、右塔轮采用的半径比应为（选填“1∶1”、“2∶1”或“3∶1”）。

查看试题解析
17. 为研究平抛物体的运动规律，某同学在水平桌面上用字典和薄木板搭成一个斜面，让小球从斜面滚下后沿桌面飞出，桌面右侧的地面上放置一个高低可调的水平木板，木板上有复写纸用来记录小球的落点。

(1)、为让小球在空中做平抛运动，下列措施正确的是____；

A、应使斜面与桌面足够光滑 B、桌面必须水平 C、应选择空心轻质小球 D、应选择质量较大、体积较小的实心小球

(2)、改变木板离地的高度，将小球从斜面上同一位置释放，落点会不同。测得当木板的离地高度为 $h_{1}$ 时，小球的水平位移为x₁；木板的离地高度为 $h_{2} (h_{2} > h_{1})$ 时，小球的水平位移为x₂。已知重力加速度为g，则小球离开桌面时速度的大小为。（用物理量的符号表示）

查看试题解析

四、解答题

18. 在飞机灭火演练中，离地 $h = 125 m$ 的高空，以大小为 $v_{0} = 60 m / s$ 的速度水平飞行的飞机，释放了一枚灭火弹，灭火弹恰好落到地面上的着火点上，如图所示。不计空气阻力，取 $g = 10 m / s^{2}$ ，求灭火弹被释放后：

(1)、在空中运动的时间；

(2)、释放点与着火点水平距离。

查看试题解析
19. 2022年6月16日凌晨，太阳系中除地球外的七颗行星将大致排列成一条直线，形成“七星连珠”的天文奇观（如图）。部分行星的质量及其与太阳的距离如下表，已知引力常量为G，忽略各星球的大小，求：
行星名称
地球
火星
木星
土星
质量/ $\times 1 0^{24} k g$
$M_{地} = 5.97$
$M_{火} = 0.64$
/
$M_{土} = 568$
日星距/AU
$r_{地} = 1$
$r_{火} = 1.52$
/
$r_{土} = 9.54$

(1)、已知地球的公转周期为1年，估算火星的公转周期；（不考虑行星间的相互作用力）

(2)、届时土星和火星间将有木星阻挡，此时土星和火星间是否还存在万有引力。如果不存在，说出理由；如果存在，写出其间万有引力大小的表达式。（用题中字母表示，不必计算数值。）

查看试题解析
20. 在一次施工中，塔吊将重物从 $O$ 点吊起，从此刻开始计时，以 $O$ 为原点，分别沿水平、竖直方向建立x轴、y轴，重物x、y方向的运动规律分别如图甲、乙所示，求：

(1)、 $t = 8 s$ 时重物速度的大小；

(2)、 $0 - t (8 s)$ 时间内重物运动的轨迹方程。

查看试题解析
21. 如图，竖立的圆轨道直径 $d = 15 m$ ，固定在地面上。一辆质量 $m = 1.2 \times 1 0^{3} k g$ 的小汽车在进行特技表演时，以某一速度冲上圆轨道，到达最高点时速度 $v_{1} = 54 k m / h$ ；之后到达最低点时速度 $v_{2} = 72 k m / h$ 。将汽车视为质点，求小汽车：（取 $g = 10 m / s^{2}$ ）

(1)、在圆轨道最高点受到的弹力；

(2)、在圆轨道最低点受到的弹力。

查看试题解析
22. 抛石机是古代战场的破城重器（如图甲），可简化为图乙所示。将石块放在长臂A端的半球形凹槽，在短臂B端挂上重物，将A端拉至地面然后突然释放，石块过最高点P时就被水平抛出。已知转轴O到地面的距离 $h = 5 m$ ， $O A = L = 15 m$ ，质量 $m = 60 k g$ 的石块从P点抛出后的水平射程达到90m，不计空气阻力和所有摩擦，取 $g = 10 m / s^{2}$ ，求：

(1)、石块落地时速度的大小；

(2)、石块到达P时对凹槽压力的大小及方向。

查看试题解析
23. 如图（俯视）所示，水平转盘可绕过圆心O的竖直轴转动，在转盘上的P点放一质量为m的小碟子，已知重力加速度为g，碟子与转盘间的动摩擦因数为μ，设最大静摩擦力等于滑动摩擦力，测得P与O的距离为r。现让转盘开始转动并缓慢增大转盘的转速，求：

(1)、当转盘的角速度为ω₁时碟子与转盘相对静止，求碟子受到的摩擦力；

(2)、当转盘的转速增大为某一值n时碟子相对转盘开始滑动，求此时转盘的转速。

查看试题解析
24. 如图所示，半径 $R = 1 m$ 的水平圆盘可绕其竖直轴转动，在圆盘的边缘关于转轴对称的两点放上质量均为m的相同小物块A、B，并将它们用轻质细线连接，当圆盘静止时，保持细线伸直且恰无张力。已知物块与圆盘间的动摩擦因数 $μ = 0.4$ ，细线可承受的最大拉力 $T_{m} = 0.5 m g$ ，认为最大静摩擦力均等于滑动摩擦力，取 $g = 10 m / s^{2}$ 。现让圆盘开始转动并缓慢增大其角速度，求：

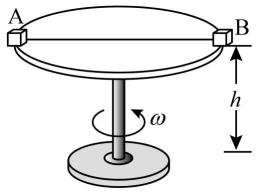(1)、细线产生弹力时圆盘的角速度 $ω_{1}$ ；

(2)、细线断裂时圆盘的角速度 $ω_{m}$ ；

(3)、已知圆盘距地面的高度 $h = \frac{15}{9} m$ ，求细线断裂后A、B落地点间的距离。

查看试题解析

行星名称	地球	火星	木星	土星
质量/ $\times 1 0^{24} k g$	$M_{地} = 5.97$	$M_{火} = 0.64$	/	$M_{土} = 568$
日星距/AU	$r_{地} = 1$	$r_{火} = 1.52$	/	$r_{土} = 9.54$