北京市房山区2021-2022学年高一下学期数学期中考试试卷

试卷更新日期：2022-04-29 类型：期中考试

进入出卷网下载

一、单选题

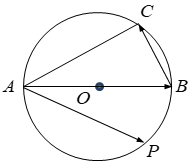
1. 将120°转化为弧度为（）

A、 $\frac{5 π}{6}$ B、 $\frac{2 π}{3}$ C、 $\frac{5}{6}$ D、 $\frac{2}{3}$

查看试题解析
2. 若角 $θ$ 满足 $t a n θ < 0$ ， $s i n θ < 0$ ，则角 $θ$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 如图，已知点 $A$ 是单位圆与 $x$ 轴的交点，角 $α$ 的终边与单位圆的交点为 $P$ ， $P M ⊥ x$ 轴于 $M$ ，过点 $A$ 作单位圆的切线交角 $α$ 的终边于 $T$ ，则角 $α$ 的正弦线、余弦线、正切线分别是（）

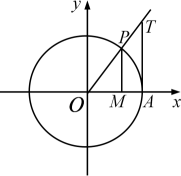A、 $\vec{O M}$ ， $\vec{A T}$ ， $\vec{M P}$ B、 $\vec{O M}$ ， $\vec{M P}$ ， $\vec{A T}$ C、 $\vec{M P}$ ， $\vec{A T}$ ， $\vec{O M}$ D、 $\vec{M P}$ ， $\vec{O M}$ ， $\vec{A T}$

查看试题解析
4. 已知扇形面积为 $\frac{3 π}{8}$ ，半径是1，则扇形的圆心角是( )

A、 $\frac{3 π}{16}$ B、 $\frac{3 π}{8}$ C、 $\frac{3 π}{4}$ D、 $\frac{3 π}{2}$

查看试题解析
5. 函数 $f (x) = t a n \frac{x}{2}$ 是（）

A、周期为 $π$ 的奇函数 B、周期为 $2 π$ 的奇函数 C、周期为 $π$ 的偶函数 D、周期为 $2 π$ 的偶函数

查看试题解析
6. 已知向量 $\vec{a} = (1 ， - 2)$ ， $\vec{b} = (t ， 1)$ ，若 $\vec{a} / / \vec{b}$ ，则 $t =$ （）

A、-1 B、 $- \frac{1}{2}$ C、 $\frac{1}{2}$ D、1

查看试题解析
7. 若角 $α$ 的终边经过点 $(3 ， 4)$ ，将角 $α$ 的终边绕原点O逆时针旋转 $\frac{π}{2}$ 与角 $β$ 的终边重合，则 $c o s β =$ （）

A、 $\frac{3}{5}$ B、 $- \frac{3}{5}$ C、 $- \frac{4}{5}$ D、 $\frac{4}{5}$

查看试题解析
8. 设 $\vec{a}$ ， $\vec{b}$ 是非零向量，则“ $| \vec{a} - \vec{b} | = | \vec{a} | + | \vec{b} |$ ”是“ $\vec{a}$ 与 $\vec{b}$ 共线”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
9. 已知角 $θ$ 与 $φ$ 都是任意角，若满足 $θ + φ = \frac{π}{2}$ ，则称 $θ$ 与 $φ$ “广义互余”．已知 $s i n (π + α) = - \frac{1}{4}$ ，下列角 $β$ 中，可能与角 $α$ “广义互余”的是（）

A、 $s i n β = \frac{1}{4}$ B、 $c o s (π - β) = \frac{1}{4}$ C、 $t a n β = \frac{\sqrt{15}}{15}$ D、 $c o s (2 π - β) = \frac{1}{4}$

查看试题解析
10. 对于函数 $f (x) = {\begin{matrix} \sin x ， \sin x \geq \cos x \\ \cos x ， \sin x < \cos x \end{matrix}$ ，给出下列四个命题：
①该函数的值域为 $[- 1 ， 1]$ ；②当且仅当 $x = 2 k π + \frac{π}{2} (k \in Z)$ 时，该函数取得最大值；③该函数是以 $π$ 为最小正周期的周期函数；④当且仅当 $2 k π + π < x < 2 k π + \frac{3 π}{2} (k \in Z)$ 时， $f (x) < 0$ .

上述命题中正确命题的个数为（）

A、 $1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析

二、填空题

11. 已知 $α = - 30 0^{∘}$ ，则与角 $α$ 终边相同的最小正角是．

查看试题解析
12. 函数 $f (x) = t a n x ， x \in [- π ， π]$ 的零点的个数是．

查看试题解析
13. 若 $c o s x = 2 m + 1$ ，且 $m \in R$ ，则 $m$ 的取值范围是．

查看试题解析
14. 已知 $O$ 是平行四边形 $A B C D$ 对角线的交点，若 $\vec{D O} = m \vec{A B} + n \vec{A C}$ ，其中 $m ， n \in R$ ，则 $m + n =$ ．

查看试题解析
15. 已知向量 $\vec{m} = (a ， b)$ ， $\vec{n} = (c ， d)$ ，规定 $\vec{m} ， \vec{n}$ 之间的一种运算 $\vec{m} ⊙ \vec{n} = (a d - b c ， a c + b d)$ .若向量 $\vec{h} = (1 ， 2)$ ，运算 $\vec{h} ⊙ \vec{k} = (3 ， 6)$ ，则向量 $\vec{k} =$ .

查看试题解析
16. 已知△ $A B C$ 为等腰直角三角形，且 $∠ A = 90 °$ .给出下列结论：
① $| \vec{A B} + \vec{A C} | = | \vec{A B} - \vec{A C} |$ ；

②| $(\vec{A B} + \vec{A C}) \cdot \vec{C B} = 0$ ；

③ $\vec{A B} - \vec{C B} = \vec{A C} - \vec{B C}$ ；

④ ${| \vec{A B} - \vec{A C} |}^{2} = {| \vec{B C} - \vec{A C} |}^{2} + {| \vec{C B} - \vec{A B} |}^{2}$ ．

其中正确结论的序号为．（写出所有正确结论的序号）

查看试题解析

三、解答题

17. 已知向量 $\vec{a} = \vec{e_{1}} - \vec{e_{2}}$ ， $\vec{b} = 2 \vec{e_{1}} + \vec{e_{2}}$ ，其中 $\vec{e_{1}} = (- 1 ， 1)$ ， $\vec{e_{2}} = (1 ， 0)$ ，求：

(1)、 $\vec{a} \cdot \vec{b}$ 和 $| \vec{a} + \vec{b} |$ 的值；

(2)、 $\vec{a}$ 与 $\vec{b}$ 的夹角 $θ$ 的余弦值．

查看试题解析
18. 已知函数 $f (x) = 2 c o s (2 x + \frac{π}{6})$ ．

(1)、求函数 $f (x)$ 的最小正周期；

(2)、求函数 $f (x)$ 的最大值，并写出 $f (x)$ 取得最大值时，自变量 $x$ 的集合；

(3)、说明由余弦曲线 $y = c o s 2 x$ 经过怎样的变换，可以得到该函数的图象.

查看试题解析
19. 已知 $\frac{π}{2} < α < π$ ， $s i n α = \frac{3}{5}$ .

(1)、求 $t a n α$ 的值；

(2)、求 $\frac{s i n (π + α) - 2 c o s (\frac{π}{2} - α)}{- s i n (- α) + c o s (π - α)}$ 的值．

查看试题解析
20. 已知函数 $f (x) = s i n (2 x + φ) (0 < φ < π)$ 的图象过点 $(\frac{π}{8} ， 1)$ .

(1)、求 $φ$ ；

(2)、求函数 $y = f (x)$ 的单调增区间；

(3)、 $\forall x \in [0 ， \frac{π}{2}]$ ， $f (x) \geq m$ 总成立．求实数 $m$ 的取值范围.

查看试题解析
21. 如图， $A B$ 是半径为 $1$ 的圆 $O$ 的直径，点 $C$ 为圆周上一点，且 $∠ A B C = 60 °$ ，点 $P$ 为圆周上一动点.

(1)、求 $\vec{A B} \cdot \vec{B C}$ 的值；

(2)、求 $\vec{A B} \cdot \vec{A P}$ 的最大值.

查看试题解析