浙江省温州十校联合体2021-2022学年高二下学期数学期中联考试卷

试卷更新日期：2022-04-29 类型：期中考试

进入出卷网下载

一、单选题

1. 设集合 $M = {1 ， 2 ， 3} ， N = {2 ， 3 ， 5}$ ，则 $M ∪ N =$ （）

A、{2，3} B、{1，2，3，5} C、{1，2，5} D、{1，5}

查看试题解析
2. “ $x > 1$ ”是“ $x > 2$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
3. 已知角α的顶点与原点O重合，始边与x轴的非负半轴重合，它的终边过点P（ $\frac{3}{5}$ ， $- \frac{4}{5}$ ），则 $s i n (π - a) + c o s (π + α)$ 的值是（）

A、 $\frac{1}{5}$ B、 $- \frac{1}{5}$ C、 $\frac{7}{5}$ D、 $- \frac{7}{5}$

查看试题解析
4. 设a，b，c是空间不同的三条直线，α，β是不同的平面，则下列推导正确的个数是（）
① $\begin{array}{l} a / / c \\ b / / c \end{array}} \Rightarrow a / / b$ ② $\begin{array}{l} a / / b \\ b \subset α \end{array}} \Rightarrow a / / α$ ③ $\begin{array}{l} a ⊥ α \\ b / / α \end{array}} \Rightarrow a ⊥ b$ ④ $\begin{array}{l} α ⊥ β \\ a \subset α \end{array}} \Rightarrow a ⊥ β$ ⑤ $\begin{array}{l} a ⊥ α \\ a ⊥ β \end{array}} \Rightarrow α / / β$

A、1 B、2 C、3 D、4

查看试题解析
5. 一半径为2米的水轮如图所示，水轮圆心O距离水面1米，已知水轮每60秒逆时针匀速转动一圈，如果当水轮上点P从水中浮现时（图中点 $P_{0}$ ）开始计时，则点P距离水面的高度h（米）与t（秒）的一个函数解析式为（）

A、 $h = 2 s i n (\frac{π}{30} t - \frac{π}{6}) + 1$ B、 $h = 2 s i n (\frac{π}{30} t - \frac{π}{3}) + 1$ C、 $h = 2 s i n (\frac{π}{30} t + \frac{π}{6}) + 1$ D、 $h = 2 s i n (\frac{π}{60} t - \frac{π}{6}) + 1$

查看试题解析
6. 下表是某饮料专卖店一天卖出奶茶的杯数y与当天气温x（单位：℃）的对比表，已知表中数据计算得到y关于x的线性回归方程为 $\hat{y} = \hat{b} x + 27$ ，则据此模型预计 $3 0^{∘} C$ 时卖出奶茶的杯数为（）
气温x/℃
5
10
15
20
25
杯数y
26
20
16
14
14

A、9 B、10 C、11 D、12

查看试题解析
7. 如图，在平面四边形ABCD中，△BCD是边长为7的等边三角形， $A D = 3 ， ∠ B A D = 12 0^{∘}$ ，则△ABC的面积为（）

A、5 $\sqrt{3}$ B、7 $\sqrt{3}$ C、10 $\sqrt{3}$ D、20 $\sqrt{3}$

查看试题解析
8. 如图，在直角梯形ABCD中， $A B / / C D$ ， $A D ⊥ A B$ ， $A B = A D = 4$ ， $C D = 2$ ， M是AD的中点，P是梯形ABCD内一点（含边界），若 $\vec{B P} = λ \vec{B M} + μ \vec{B C}$ ，且 $λ + 2 μ = 1$ ，则 $\vec{P M} \cdot \vec{P C}$ 的最小值是（）

A、-7 B、-2 C、-1 D、0

查看试题解析

二、多选题

9. 下列计算正确的是（）

A、 ${(2^{\frac{1}{4}})}^{2} = \sqrt{2}$ B、 $l g 2 + l g 5 = 1$ C、 $e^{2 l n 3} = 6$ D、 $l o g_{2} 3 \cdot l o g_{3} 4 \cdot l o g_{4} 8 = 3$

查看试题解析
10. 如图是一个正方体的表面展开图，还原成正方体后，下列判断正确的是（）

A、AC∥FH B、BG与FH所成的角为60° C、二面角G—AB—C的大小为45° D、B，D，E，G恰好是一个正四面体的四个顶点

查看试题解析
11. 下列结论正确的是（）

A、若随机变量 $X ∼ N (0 ， 1)$ ，则 $P (x \leq - 1) = P (x \geq 1)$ B、已知随机变量X，Y满足 $X + 2 Y = 8$ ，若 $X ∼ B (10 ， 0.6)$ ，则 $E (Y) = 1 ， D (Y) = 1.2$ C、某中学志愿者协会有6名男同学，4名女同学，现从这10名同学中随机选取3名同学去参加某公益活动（每位同学被选到的可能性相同）.则至少选到2名女同学的概率是0.3 D、三批同种规格的产品，第一批占20%，第二批占30%，第一批占50%，次品率依次为6%、5%、4%，将三批产品混合，从混合产品中任取1件，则这件产品是合格品的概率是0.953

查看试题解析
12. 已知 $a > 0 ， b > 0$ ，且 $a + b = 1$ ，则（）

A、ab的最大值为 $\frac{1}{4}$ B、 $\frac{1}{a} + \frac{2}{b}$ 的最小值为 $3 + 2 \sqrt{2}$ C、 $a^{2} + b^{2}$ 的最小值为 $\frac{1}{2}$ D、 $(a + 1) (2 b + 1)$ 的最大值为3

查看试题解析

三、填空题

13. 若复数z满足 $(1 + 2 i) z - i = 3$ （i是虚数单位），则 $| z | =$ .

查看试题解析
14. 在 $(\frac{2}{x} + \sqrt{x})^{7}$ 的展开式中 $x^{- 1}$ 的系数为.

查看试题解析
15. 从2，4，6，8中任取3个数字，从1，3，5，7，9中任取2个数字，一共可以组成个没有重复数字的五位偶数（用数字作答）.

查看试题解析
16. 已知函数 $f (x) = {(x^{2} + \frac{1}{x^{2}} + 9 - m)}^{2} + {(m - a x - \frac{a}{x})}^{2}$ 对任意 $m \in R$ 和任意 $x \in [\frac{1}{2} ， 2]$ 都有 $f (x) \geq 2$ 恒成立，则实数a的取值范围是.

查看试题解析

四、解答题

17. 在平面直角坐标系中，已知向量 $\vec{a} = (\sqrt{3} ， 1 ）， \vec{b} = (c o s x ， - s i n x) ， x \in (0 ， π)$

(1)、若 $\vec{a} / / \vec{b}$ ，求x的值；

(2)、若 $\vec{a}$ 与 $\vec{b}$ 夹角为 $\frac{π}{3}$ ，求x的值.

查看试题解析
18. 为激活国内消费市场，挽回疫情造成的损失，国家出台一系列的促进国内消费的优惠政策.某机构从某一电商的线上交易大数据中来跟踪调查消费者的购买力，现从电商平台消费人群中随机选出200人，并将这200人按年龄分组，记第1组[15，25），第2组[25，35），第3组[35，45），第4组[45，55），第5组[55，65），得到如下频率分布直方图：

(1)、求出频率分布直方图中的a值和这200人的年龄的众数、中位数及平均数；

(2)、从第1，2组中用分层抽样的方法抽取10人，并再从这10人中随机抽取2人进行电话回访，求这两人恰好属于同一组别的概率；

查看试题解析
19. 在△ABC中，角A，B，C的对边分别为a，b，c，且 $a^{2} + c^{2} - b^{2} = \sqrt{3} a c$ ， $2 a c o s C = 2 b + c$ .

(1)、求△ABC各内角的大小；

(2)、若D，E是边BC上的两点， $∠ D A E = \frac{π}{3}$ ， $b = 2$ ，设 $∠ B A D = α$ ， △ADE的面积为f（a），求函数f（a）的最小值.

查看试题解析
20. 如图，在四面体ABCD中， $A B = A C = B D = C D = B C = 2$ ， $A D = \sqrt{3}$ ， M是棱AD的中点.

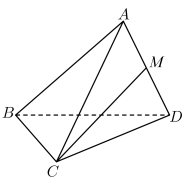(1)、求四面体ABCD的表面积和体积；

(2)、求直线CM与底面BCD所成的角的正弦值.

查看试题解析

21. 某中学为了解中学生的课外阅读时间，决定在该中学抽取20名学生，对他们的课外阅读A类（不参加课外阅读），B类（参加课外阅读，但平均每周参加课外阅读的时间不超过3小时），C类（参加课外阅读，且平均每周参加课外阅读的时间超过3小时）.调查结果如下表：

	A类	B类	C类
男生	3	5	4
女生	1	3	4

附： $x^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$

a	0.1	0.05	0.01	0.005	0.001
x₀	2.706	3.841	6.635	7.897	10.828

(1)、根据表中的统计数据，完成下面的列联表，并判断是否有90%的把握认为“参加课外阅读与否”与性别有关；

	男生	女生	总计
不参加课外阅读
参加课外阅读
总计

(2)、从抽出女生中再随机抽取3人进一步了解情况，记X为抽取的这3名女生中B类人数和C类人数差的绝对值，求随机变量X的分布列和均值（数学期望）.

查看试题解析

22. 已知函数 $f (x) = x^{2} - a | x | + b$ ， $g (x) = c o s 2 x + (2 a - 1) c o s x + 1 - a (a ， b \in R)$

(1)、判断 $f (x)$ 的奇偶性并证明；

(2)、若 $a = 1 ， x \in [0 ， π]$ ，求 $g (x)$ 的最小值和最大值；

(3)、定义 $m i n {x ， y} = {\begin{array}{l} x ， x \leq y \\ y ， x > y \end{array}$ ，设 $h (x) = m i n {f (x) ， g (x)}$ .若 $h (x)$ 在 $(- \frac{π}{2} ， \frac{π}{2})$ 内恰有三个不同的零点，求a的取值集合.

查看试题解析

气温x/℃	5	10	15	20	25
杯数y	26	20	16	14	14