江西省赣州市十六县(市)十九校2021-2022学年高二下学期理数期中考试试卷
试卷更新日期:2022-04-29 类型:期中考试
一、单选题
-
1. 为虚数单位,( )A、 B、 C、-1 D、12. 设 存在导函数且满足 ,则曲线 上的点 处的切线的斜率为( )A、-1 B、-2 C、1 D、23. ( )A、8π B、4π C、2π D、π4. 空间中,与向量同向共线的单位向量为( )A、 B、或 C、 D、或5. “干支(gàn zhī)纪年法”是中国历法上自古以来就一直使用的纪年方法,干支是天干和地支的总称.甲、乙、丙、丁、戊、己、庚、辛、壬、癸十个符号叫天干,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥十二个符号叫地支,干支按序相配,组成干支纪年法,相配顺序为甲子、乙丑、丙寅…癸酉;甲戌、乙亥、丙子…癸未;甲申、乙酉、丙戌…癸巳;……共得60种不同组合,这就是俗称的“六十甲子”,也叫“干支表”,周而复始干支纪年以每年立春换年,是中华民族的伟大发明.2022年是干支纪年中的壬寅年,则2036年是干支纪年中的( )A、甲寅年 B、乙卯年 C、丙辰年 D、甲巳年6. 已知函数 , 则=( )A、21 B、20 C、16 D、117. 用数学归纳法证明 时,第一步应验证不等式( )A、 B、 C、 D、8. 已知函数f(x)= x2+cosx,f'(x)是函数f(x)的导函数,则f'(x)的图象大致是( )A、
 B、
B、 C、
C、 D、
D、 9. 对于三次函数 , 给出定义:设是函数的导数,是的导数.若方程有实数解 , 则称点为函数的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数 , 则( )A、0 B、1 C、2 D、310. 如图,已知多面体 , 其中是边长为4的等边三角形,四边形是矩形, , 平面平面 , 则点到平面的距离是( )
9. 对于三次函数 , 给出定义:设是函数的导数,是的导数.若方程有实数解 , 则称点为函数的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数 , 则( )A、0 B、1 C、2 D、310. 如图,已知多面体 , 其中是边长为4的等边三角形,四边形是矩形, , 平面平面 , 则点到平面的距离是( )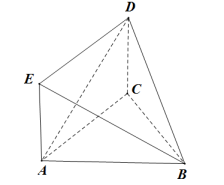 A、 B、 C、 D、11. 设直线 与双曲线 两条渐近线分别交于点 , ,若点 满足 ,则该双曲线的渐近线方程是( )A、 B、 C、 D、12. 已知函数 的导函数为 , 为自然对数的底数,对 均有 成立,且 ,则不等式 的解集是( )A、 B、 C、 D、
A、 B、 C、 D、11. 设直线 与双曲线 两条渐近线分别交于点 , ,若点 满足 ,则该双曲线的渐近线方程是( )A、 B、 C、 D、12. 已知函数 的导函数为 , 为自然对数的底数,对 均有 成立,且 ,则不等式 的解集是( )A、 B、 C、 D、二、填空题
-
13. 设复数满足 , 则 .14. 已知函数在上不单调,则实数t的取值范围是 .15. 已知椭圆与双曲线有相同的焦点 , 且两曲线在第一象限的交点为P,若 , 且 , 则双曲线的离心率为 .16. 体积为8的四棱锥的底面是边长为的正方形,四棱锥的外接球球心O到底面ABCD的距离为2,则点P的轨迹长度为.
三、解答题
-
17. 已知a为实数,函数 , .(1)、求a的值;(2)、求函数在上的极值.18. 如图,已知四棱锥的底面是矩形,平面ABCD, , 点E是棱AD上的一点,且 , 点F是棱PC上的一点,且 .
 (1)、求证:平面PEB;(2)、求直线PC与平面PEB所成角的正弦值.19. 已知抛物线上一点到焦点的距离与到轴的距离相等.(1)、求抛物线的方程;(2)、若直线与抛物线交于A,两点,且满足(为坐标原点),证明:直线与轴的交点为定点.
(1)、求证:平面PEB;(2)、求直线PC与平面PEB所成角的正弦值.19. 已知抛物线上一点到焦点的距离与到轴的距离相等.(1)、求抛物线的方程;(2)、若直线与抛物线交于A,两点,且满足(为坐标原点),证明:直线与轴的交点为定点.
