山东省青岛市市北区2021-2022学年下学期期中质量检测数学试题(一模)
试卷更新日期:2022-04-29 类型:中考模拟
一、单选题
-
1. 下列四个数中,属于有理数的是( )A、 B、 C、 D、2. 2022年2月4日至20日,第24届冬奥会在北京和张家口举办,北京是唯一同时举办过夏季和冬季奥运会的城市.下列4个图像是四届冬奥会的部分图标,属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 2021年11月3日揭晓的2020年度国家自然科学奖,共评出了两项一等奖,其中一项是“有序介孔高分子和碳材料的创制应用”.有序介孔材料是上世纪90年代迅速兴起的新型纳米材料,孔径在0.000000002米~0.000000005米范围内.数据0.000000005用科学记数法可表示为( )A、5×10-9 B、5×10-8 C、5×10-7 D、0.5×10-74. 在如图各选项中,可以由左边的平面图形折成右边的封闭立体图形的是( )A、
3. 2021年11月3日揭晓的2020年度国家自然科学奖,共评出了两项一等奖,其中一项是“有序介孔高分子和碳材料的创制应用”.有序介孔材料是上世纪90年代迅速兴起的新型纳米材料,孔径在0.000000002米~0.000000005米范围内.数据0.000000005用科学记数法可表示为( )A、5×10-9 B、5×10-8 C、5×10-7 D、0.5×10-74. 在如图各选项中,可以由左边的平面图形折成右边的封闭立体图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,AB是⊙O 的直径,C、F为⊙O 上的点,AE是⊙O 的切线,A为切点,连接BC并延长交AE于点D.若∠ADB=50°,则∠BFC 的度数为( )
5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,AB是⊙O 的直径,C、F为⊙O 上的点,AE是⊙O 的切线,A为切点,连接BC并延长交AE于点D.若∠ADB=50°,则∠BFC 的度数为( ) A、40° B、50° C、60° D、20°7. 若一元二次方程有两个不相等的实数根,则二次函数的图象与一次函数在同一平面直角坐标系中的图象可能是( )A、
A、40° B、50° C、60° D、20°7. 若一元二次方程有两个不相等的实数根,则二次函数的图象与一次函数在同一平面直角坐标系中的图象可能是( )A、 B、
B、 C、
C、 D、
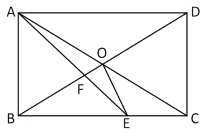
D、 8. 如图,在矩形ABCD中,AC、BD相交于点O,∠AOB=60°,AE平分∠BAD,AE与BC相交于点E,与BD相交于点F.则下列结论中正确的有( )
8. 如图,在矩形ABCD中,AC、BD相交于点O,∠AOB=60°,AE平分∠BAD,AE与BC相交于点E,与BD相交于点F.则下列结论中正确的有( )①OB=OE;②∠BOE=75°;③OE2=OF•OD ;④若OE=1,则EC=;⑤若△BOE的面积是矩形ABCD的面积的 , 则BC=AB .
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
9. 计算:•cos30°= .10. 某大型商场为了吸引顾客,规定凡在本商场一次性消费100元的顾客可以参加一次摇奖活动,摇奖规则如下:一个不透明的纸箱里装有1个红球、2个黄球、5个绿球、12个白球,所有除颜色外完全相同.充分摇匀后,从中随机抽取出一球,若取出的球分别是红、黄、绿球,顾客将分别获得50元、25元、20元现金,若取出白球则没有奖.若某位顾客有机会参加摇奖活动,则他每参与一次的平均收益为元.11. 若一个圆内接正六边形的边长是4cm,则这个正六边形的边心距=cm.12. 高铁为居民出行提供了便利,从铁路沿线相距360公里的甲地到乙地,乘坐高铁列车比乘坐普通列车少用3小时.已知高铁列车的平均速度是普通列车平均速度的3倍,设普通列车的平均速度为x公里/小时,则根据题意可得方程 .13. 如图,正比例函数y=kx与反比例函数y= 的图象有一个交点A(2,m),AB⊥x轴于点B,平移直线y=kx使其经过点B,得到直线l,则直线l对应的函数表达式是 .
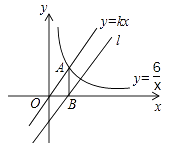 14. 如图所示,在扇形OAB中,∠AOB=90°,半径OA=4,点F位于弧AB的处,且靠近点A的位置.点C、D分别在线段OA、OB上,CD=4,E为CD的中点,连接EF、BE.在CD滑动过程中(CD长度始终保持不变),当EF取最小值时,阴影部分的面积为 .
14. 如图所示,在扇形OAB中,∠AOB=90°,半径OA=4,点F位于弧AB的处,且靠近点A的位置.点C、D分别在线段OA、OB上,CD=4,E为CD的中点,连接EF、BE.在CD滑动过程中(CD长度始终保持不变),当EF取最小值时,阴影部分的面积为 .
三、解答题
-
15. 如图是一张形状为四分之一圆的纸片,要在纸片上裁剪出一个尽可能大的正方形,请你在图中做出这个正方形.
 16. 计算(1)、化简:;(2)、解不等式组 .17. 某校组建了射击兴趣小组,甲、乙两人连续8次射击成绩如下列图、表所示(统计图中乙的第8次射击成绩缺失).
16. 计算(1)、化简:;(2)、解不等式组 .17. 某校组建了射击兴趣小组,甲、乙两人连续8次射击成绩如下列图、表所示(统计图中乙的第8次射击成绩缺失).
甲、乙两人连续射击8次成绩统计表
平均成绩(环)
中位数(环)
方差(环2)
甲
7.5
乙
6
3.5
(1)、乙的第8次射击成绩是环;(2)、补全统计图;(3)、如果你是教练,要从甲、乙两人中选一位参加比赛,你会选择谁?写出你这样选择的2条理由.18. 小亮是个集邮爱好者,他收集了如图所示的四张纪念邮票(除正面内容不同外,其余均相同),现将四张邮票背面朝上,洗匀放好 (1)、小亮从中随机抽取一张邮票是“冬奥会吉祥物冰墩墩”的概率是(2)、小亮从中随机抽取一张邮票(不放回),再从余下的邮票中随机抽取一张,求抽到的两张邮票恰好是“冬奥会会徽”和“冬奥会吉祥物冰墩墩”的概率.(这四张邮票从左到右依次分别用字母A、B、C、D表示)19. 矗立在高速公路水平地面上的交通示警牌如图所示,测量得到如下数据:∠B=90°,∠BDC=72°,∠E=35°,CD=2.8米,BE=7.5米.求线段AC的长.(结果精确到0.1米)
(1)、小亮从中随机抽取一张邮票是“冬奥会吉祥物冰墩墩”的概率是(2)、小亮从中随机抽取一张邮票(不放回),再从余下的邮票中随机抽取一张,求抽到的两张邮票恰好是“冬奥会会徽”和“冬奥会吉祥物冰墩墩”的概率.(这四张邮票从左到右依次分别用字母A、B、C、D表示)19. 矗立在高速公路水平地面上的交通示警牌如图所示,测量得到如下数据:∠B=90°,∠BDC=72°,∠E=35°,CD=2.8米,BE=7.5米.求线段AC的长.(结果精确到0.1米)(参考数据:sin35° , cos35° , tan35° , sin72° , cos72° , tan72°)
 20. 崂山茶是青岛的特产之一,某崂山茶企业为了扩大生产规模,计划投入一笔资金购进甲、乙两种设备.已知购进2件甲设备和1件乙设备共需3.5万元;购进1件甲设备和3件乙设备共需3万元.(1)、求购进1件甲设备和1件乙设备分别需要多少万元;(2)、如果扩大规模后,在一个季度内,每件甲设备能为企业增加0.5万元利润,每件乙设备能为企业增加0.2万元利润.该企业计划购进甲、乙两种设备共10件,且投入资金不超过12万元,求应该如何采购甲、乙两种设备,才能使企业这个季度的利润最大?21. 如图,延长平行四边形ABCD的边AD到F,使DF=AD,连接BF,交DC于点E,延长CD至点G,使DG=DE,分别连接AE、AG、FG.
20. 崂山茶是青岛的特产之一,某崂山茶企业为了扩大生产规模,计划投入一笔资金购进甲、乙两种设备.已知购进2件甲设备和1件乙设备共需3.5万元;购进1件甲设备和3件乙设备共需3万元.(1)、求购进1件甲设备和1件乙设备分别需要多少万元;(2)、如果扩大规模后,在一个季度内,每件甲设备能为企业增加0.5万元利润,每件乙设备能为企业增加0.2万元利润.该企业计划购进甲、乙两种设备共10件,且投入资金不超过12万元,求应该如何采购甲、乙两种设备,才能使企业这个季度的利润最大?21. 如图,延长平行四边形ABCD的边AD到F,使DF=AD,连接BF,交DC于点E,延长CD至点G,使DG=DE,分别连接AE、AG、FG. (1)、求证:△BCE≌△FDE;(2)、当平行四边形ABCD的边或角满足什么条件时,四边形AEFG是菱形?证明你的结论.22. 手榴弹作为一种威力较大,体积较小,方便携带的武器,在战争中能发挥重要作用,然而想把手榴弹扔远,并不是一件容易的事.军训中,借助小山坡的有利地势,小刚在教官的指导下用模拟弹进行一次试投:如图所示,把小刚投出的手榴弹的运动路线看做一条抛物线,手榴弹飞行的最大高度为12米,此时它的水平飞行距离为6米,山坡OA的坡度为1:3.
(1)、求证:△BCE≌△FDE;(2)、当平行四边形ABCD的边或角满足什么条件时,四边形AEFG是菱形?证明你的结论.22. 手榴弹作为一种威力较大,体积较小,方便携带的武器,在战争中能发挥重要作用,然而想把手榴弹扔远,并不是一件容易的事.军训中,借助小山坡的有利地势,小刚在教官的指导下用模拟弹进行一次试投:如图所示,把小刚投出的手榴弹的运动路线看做一条抛物线,手榴弹飞行的最大高度为12米,此时它的水平飞行距离为6米,山坡OA的坡度为1:3. (1)、求这条抛物线的表达式;(2)、山坡上A处的水平距离OE为9米,A处有一棵树,树高5米,则小刚投出的手榴弹能否越过这棵树?请说明理由;(3)、求飞行的过程中手榴弹离山坡的最大高度是多少米.23. 定义:
(1)、求这条抛物线的表达式;(2)、山坡上A处的水平距离OE为9米,A处有一棵树,树高5米,则小刚投出的手榴弹能否越过这棵树?请说明理由;(3)、求飞行的过程中手榴弹离山坡的最大高度是多少米.23. 定义:如果一个正整数n能表示为两个正整数的平方差,那么称正整数n为“智慧数”,即:若正整数n=a2-b2(a,b为正整数,且a>b),则称正整数n为“智慧数”.例如:∵5=32-22 , ∴5是“智慧数”.根据定义,直接写出最小的“智慧数”是 .
提出问题:
如果按照从小到大的顺序排列起来,那么第2022个“智慧数”是哪位数?
探究问题:
要解答这个问题,我们先要明白“智慧数”产生的规律.
探究1:“智慧数”一定是什么数?
假设n是“智慧数”,则至少存在一组正整数a、b,使n=a2-b2(a,b为正整数,且a>b).
情况1:a、b均为奇数,或均为偶数.
分析:
∵a、b均为奇数,或均为偶数
∴(a+b)、(a-b)均为偶数
此时不妨设(a+b)=2c,(a-b)=2d
又∵n=a2-b2=(a+b)(a-b)=4cd
∴a2-b2为4的倍数,即n为4的倍数.
情况2:a、b为一奇数、一偶数.
分析:
∵a、b为一奇数、一偶数
∴(a+b)、(a-b)均为奇数
此时不妨设(a+b)=2c1,(a-b)=2d1
又∵n=a2-b2=(a+b)(a-b)=4cd2c2d1
∴a2-b2为奇数,即n为奇数.
综上所述:“智慧数”为奇数或4的倍数.
探究2:所有奇数和4的倍数都一定“智慧数”吗?
我们先从最简单的情形入手,从中找到解决问题的方法,最后得出一般性的结论.
先举例几组数值较小,容易验证的“智慧数”(①--⑧),因为“智慧数”不是奇数就是4的倍数,所以我们把这“智慧数”分成两类.
情况1:n是奇数
分析n=a2-b2
结论
①
3是“智慧数”
②
5是“智慧数”
③
7是“智慧数”
④
9是“智慧数”
……
……
……
情况2:n是4的倍数
分析n=a2-b2
结论
⑤
8是“智慧数”
⑥
12是“智慧数”
⑦
16是“智慧数”
⑧
20是“智慧数”
……
……
……
情况1:n是奇数
观察①②③④中n、a、b的值,容易发现,每个算式中,n均是奇数,且a、b的值均为连续的正整数.
猜想:所有奇数都是“智慧数”.
验证:设a=k+1,b=k(k≥1,且k为整数)
∵a2-b2=(k+1)2-k2=2k+1
∴2k+1是“智慧数”
又∵k≥1
∴2k+1≥3,即2k+1表示所有奇数(1除外)
∴所有奇数(1除外)都是“智慧数”
应用:
请直接填空:∵11= 2-2 ∴11是“智慧数”
情况2:n是4的倍数.
观察⑤⑥⑦⑧中n、a、b的值,容易发现,每个算式中,n均是4的倍数,且a、b的差都为2.
猜想:所有4的倍数都是“智慧数”.
验证:设a=k+2,b=k(k≥1,且k为整数)
∵a2-b2=(k+2)2-k2=4k+4
∴4k+4是“智慧数”
又∵k≥1
∴4k+4≥8,即4k+4表示所有4的倍数(4除外)
∴所有4的倍数(4除外)都是“智慧数”
应用:
请直接填空:∵24= 2- 2 ∴24“智慧数”
归纳“智慧数”的发现模型:
⑴对所有的正整数而言,除了1和4之外,其余的奇数以及4的倍数是智慧数.
⑵当1≤n≤4时,只有1个“智慧数”;
当n≥5时,如果把从5开始的正整数按照从小到大的顺序,依次每个连续正整数分成一组(注:组与组之间的数字互不重复),则每组有个“智慧数”,且第个数不是“智慧数”.
问题解决:
直接写出:如果按照从小到大的顺序排列起来,那么第2022个“智慧数”是 .
实际应用:
若一个直角三角形纸片三边的长度都是整数厘米,已知一条直角边长是12cm,则这个直角三角形纸片的周长最大是cm.
24. 如图,在△ABC中,∠ACB=90°,AC=12,BC=9,点D为边AB的中点.点P从点A出发,沿AC方向以每秒1个单位的速度向终点C运动;同时点Q从点C出发,以每秒2个单位的速度沿CB方向运动,以DP、DQ为邻边构造平行四边形PEQD.设点P运动的时间为t秒, . (1)、求当t为何值时,?(2)、设平行四边形PEQD的面积为S(),求S关于t之间的函数关系式;(3)、连接CD,是否存在某一时刻t,CD经过平行四边形PEQD的对称中心O?若存在,求出t的值;若不存在,请说明理由;
(1)、求当t为何值时,?(2)、设平行四边形PEQD的面积为S(),求S关于t之间的函数关系式;(3)、连接CD,是否存在某一时刻t,CD经过平行四边形PEQD的对称中心O?若存在,求出t的值;若不存在,请说明理由;