山东省菏泽市牡丹区2021-2022年九年级下学期3月月考数学试题(一模)
试卷更新日期:2022-04-29 类型:中考模拟
一、单选题
-
1. 若与是同类项,则( )A、-1 B、7 C、1 D、02. 如果关于 的一元二次方程 有两个不相等的实数根,那么 的取值范围是( )
A、 B、 且 C、 D、 且3. 关于函数的图象,下列结论正确的是( )A、必经过点(1,2) B、与x轴交点的坐标为(0,-4) C、过第一、三、四象限 D、可由函数的图象平移得到4. 如图,在中, , , , 将绕一逆时针方向旋转40°,得到 , 点B经过的路径为弧BD,则图中阴影部分的面积为( )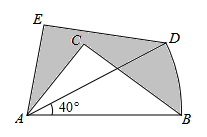 A、 B、 C、 D、5. 如图,PA,PB分别与⊙O相切于A,B两点,点C为⊙O上一点,连接AC,BC,若∠P=50°,则∠ACB的度数为( ).
A、 B、 C、 D、5. 如图,PA,PB分别与⊙O相切于A,B两点,点C为⊙O上一点,连接AC,BC,若∠P=50°,则∠ACB的度数为( ).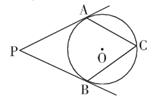 A、60° B、75° C、70° D、65°6. 以下四个命题中,真命题的个数为( )
A、60° B、75° C、70° D、65°6. 以下四个命题中,真命题的个数为( )
(1)已知等腰△ABC中,AB=AC,顶角∠A=36°,一腰AB的垂直平分线交AC于点E,AB 为点D,连接BE,则∠EBC的度数为36°;(2)经过一点有且只有一条直线与这条直线平行;(3)长度相等的弧是等弧;(4)顺次连接菱形各边得到的四边形是矩形.A、1个 B、2个 C、3个 D、4个7. 对一组数据:2,1,3,2,3分析错误的是( )A、平均数是2.2 B、方差是4 C、众数是3和2 D、中位数是28. 如图,CE是□ABCD的边AB的垂直平分线,垂足为点O , CE与DA的延长线交于点E、连接AC , BE , DO , DO与AC交于点F , 则下列结论:①四边形ACBE是菱形;②∠ACD=∠BAE;③AF:BE=2:3;④S四边形AFOE:S△COD=2:3.其中正确的结论有( )个.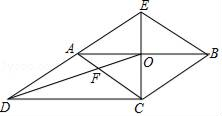 A、1 B、2 C、3 D、49. 参加足球联赛的每两支球队之间都要进行两场比赛,共要比赛110场,设参加比赛的球队有x支,根据题意,下面列出的方程正确的是( )A、 x(x+1)=110 B、 x(x﹣1)=110 C、x(x+1)=110 D、x(x﹣1)=11010. 二次函数的图象如图所示,其对称轴为直线 , 与x轴的交点为、 , 其中 , 有下列结论:①;②;③;④当m为任意实数时,;⑤ . 其中,正确的结论有( )
A、1 B、2 C、3 D、49. 参加足球联赛的每两支球队之间都要进行两场比赛,共要比赛110场,设参加比赛的球队有x支,根据题意,下面列出的方程正确的是( )A、 x(x+1)=110 B、 x(x﹣1)=110 C、x(x+1)=110 D、x(x﹣1)=11010. 二次函数的图象如图所示,其对称轴为直线 , 与x轴的交点为、 , 其中 , 有下列结论:①;②;③;④当m为任意实数时,;⑤ . 其中,正确的结论有( )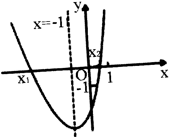 A、①③④ B、①③⑤ C、②④⑤ D、①④⑤
A、①③④ B、①③⑤ C、②④⑤ D、①④⑤二、填空题
-
11. 直线y=x+4与x轴、y轴分别交于点A和点B,在x轴上取点C,使△ABC为等腰三角形,则点C的坐标是 .12. 如图,直角三角形的直角顶点在坐标原点, ,若点 在反比例函数 的图象上,则经过点 的反比例函数解析式为;
 13. 如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则cos∠AOD= .
13. 如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则cos∠AOD= .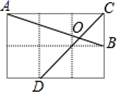 14. 如图,在平面直角坐标系中,点A,C分别在x轴、y轴上,四边形ABCO是边长为4的正方形,点D为AB的中点,点P为OB上的一个动点,连接DP,AP,当点P满足DP+AP的值最小时,直线AP的解析式为.
14. 如图,在平面直角坐标系中,点A,C分别在x轴、y轴上,四边形ABCO是边长为4的正方形,点D为AB的中点,点P为OB上的一个动点,连接DP,AP,当点P满足DP+AP的值最小时,直线AP的解析式为.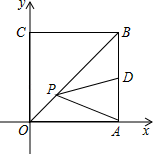 15. 在平面直角坐标系中,正方形的位置如图所示,点的坐标为 , 点的坐标为 , 延长交轴于点 , 作正方形;延长交轴于点 , 作正方形;…,按照这样的规律作正方形,则点的纵坐标为 .
15. 在平面直角坐标系中,正方形的位置如图所示,点的坐标为 , 点的坐标为 , 延长交轴于点 , 作正方形;延长交轴于点 , 作正方形;…,按照这样的规律作正方形,则点的纵坐标为 .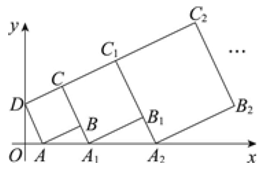
三、解答题
-
16. 计算: + ﹣( )﹣2+|3﹣ |.17. 先化简,再求值:
, 其中的值从不等式组的整数解中选取.
18. 如今很多初中生喜欢购买饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此某班数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:A:白开水,B:瓶装矿泉水,C:碳酸饮料,D:非碳酸饮料,根据统计结果绘制如下两个不完整的统计图,根据统计图提供的信息,解答下列问题: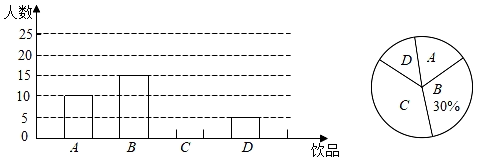 (1)、这个班级有 ▲ 名同学;并补全条形统计图;(2)、若该班同学每人每天只饮用一种饮品(每种仅限一瓶,价格如表),则该班同学每天用于饮品的人均花费是多少元?
(1)、这个班级有 ▲ 名同学;并补全条形统计图;(2)、若该班同学每人每天只饮用一种饮品(每种仅限一瓶,价格如表),则该班同学每天用于饮品的人均花费是多少元? (3)、在饮用白开水的同学中有4名班委干部,为了养成良好的生活习惯,班主任决定在这4名班委干部(其中有两位班长记为A,B,其余两位记为C,D)中随机抽取2名作为良好习惯监督员,请用列表法或画树状图的方法,求出恰好抽到2名班长的概率.19. 如图:在平面直角坐标系中,菱形 的顶点D在y轴上,A,C两点的坐标分别为 ,直线 与双曲线: 交于C, 两点.
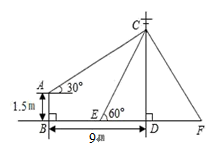
(3)、在饮用白开水的同学中有4名班委干部,为了养成良好的生活习惯,班主任决定在这4名班委干部(其中有两位班长记为A,B,其余两位记为C,D)中随机抽取2名作为良好习惯监督员,请用列表法或画树状图的方法,求出恰好抽到2名班长的概率.19. 如图:在平面直角坐标系中,菱形 的顶点D在y轴上,A,C两点的坐标分别为 ,直线 与双曲线: 交于C, 两点.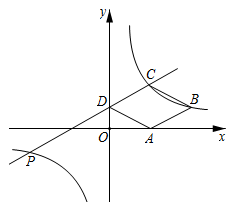 (1)、求双曲线 的函数关系式及m的值;(2)、判断点B是否在双曲线上,并说明理由;(3)、当 时,请直接写出x的取值范围.20. 如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆9m的B处安置高为1.5m的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长.(结果保留根号)
(1)、求双曲线 的函数关系式及m的值;(2)、判断点B是否在双曲线上,并说明理由;(3)、当 时,请直接写出x的取值范围.20. 如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆9m的B处安置高为1.5m的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长.(结果保留根号)
 21. “燃情冰雪,拼出未来”,北京冬奥会将于2022年2月4日如约而至.某商家已提前开始冬奥会吉祥物“冰墩墩”纪念品的销售.每个纪念品进价40元,规定销售单价不低于44元,且不高于52元.销售期间发现,当销售单价定为44元时,每天可售出300个,销售单价每上涨1元,每天销量减少10个.现商家决定提价销售,设每天销售量为个,销售单价为元.(1)、直接写出与之间的函数关系式和自变量的取值范围;(2)、求当每个纪念品的销售单价是多少元时,商家每天获利2400元;(3)、将纪念品的销售单价定为多少元时,商家每天销售纪念品获得的利润元最大?最大利润是多少元?22. 如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC的延长线于点E,交AB的延长线于点F.
21. “燃情冰雪,拼出未来”,北京冬奥会将于2022年2月4日如约而至.某商家已提前开始冬奥会吉祥物“冰墩墩”纪念品的销售.每个纪念品进价40元,规定销售单价不低于44元,且不高于52元.销售期间发现,当销售单价定为44元时,每天可售出300个,销售单价每上涨1元,每天销量减少10个.现商家决定提价销售,设每天销售量为个,销售单价为元.(1)、直接写出与之间的函数关系式和自变量的取值范围;(2)、求当每个纪念品的销售单价是多少元时,商家每天获利2400元;(3)、将纪念品的销售单价定为多少元时,商家每天销售纪念品获得的利润元最大?最大利润是多少元?22. 如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC的延长线于点E,交AB的延长线于点F.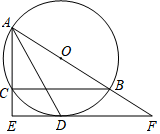 (1)、求证:EF是⊙O的切线;(2)、若AC=8,CE=4,求弧BD的长.(结果保留π)23. 已知:正方形中, , 将绕点A顺时针旋转,它的两边分别交、(或它们的延长线)于点M、N.
(1)、求证:EF是⊙O的切线;(2)、若AC=8,CE=4,求弧BD的长.(结果保留π)23. 已知:正方形中, , 将绕点A顺时针旋转,它的两边分别交、(或它们的延长线)于点M、N.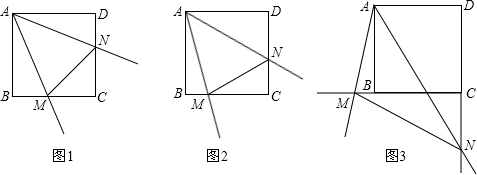 (1)、如图1,当绕点A旋转到时,有 . 当绕点A旋转到时,如图2,请问图1中的结论还是否成立?如果成立,请给予证明,如果不成立,请说明理由;(2)、当绕点A旋转到如图3的位置时,线段和之间有怎样的等量关系?请写出你的猜想,并证明.24. 如图,已知二次函数的图象与坐标轴交于点和点 .
(1)、如图1,当绕点A旋转到时,有 . 当绕点A旋转到时,如图2,请问图1中的结论还是否成立?如果成立,请给予证明,如果不成立,请说明理由;(2)、当绕点A旋转到如图3的位置时,线段和之间有怎样的等量关系?请写出你的猜想,并证明.24. 如图,已知二次函数的图象与坐标轴交于点和点 .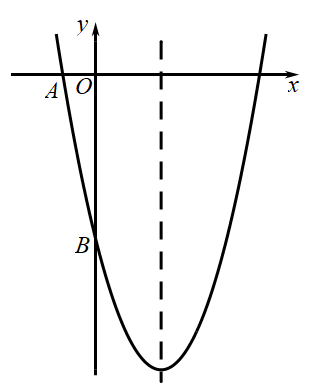 (1)、求该二次函数的解析式;(2)、已知该函数图象的对称轴上存在一点 , 使得的周长最小.请求出点的坐标;(3)、在(2)的条件下,在轴上找一点 , 使得是等腰三角形,请直接写出所有符合条件的点的坐标.
(1)、求该二次函数的解析式;(2)、已知该函数图象的对称轴上存在一点 , 使得的周长最小.请求出点的坐标;(3)、在(2)的条件下,在轴上找一点 , 使得是等腰三角形,请直接写出所有符合条件的点的坐标.