黑龙江省大庆市肇州县2021-2022年九年级下学期第一次联考数学试题(一模)
试卷更新日期:2022-04-29 类型:中考模拟
一、单选题
-
1. 在这四个数中,最小的数是( )A、 B、-1 C、 D、02. “多少事,从来急;天地转,光阴迫.一万年太久,只争朝夕.”伟人毛泽东通过这首《满江红•和郭沬若同志》告诉我们青年学生:要珍惜每分每秒;努力工作,努力学习.一天时间为86400秒,用科学记数法表示这一数字是( )A、864×102 B、86.4×103 C、8.64×104 D、0.864×1053. 下列结论正确的是( )A、如果a>b,c>d,那么a﹣c>b﹣d B、如果a>b,那么 C、如果a>b,那么 D、如果 , 那么a<b4. 如图是每个面上都有一个汉字的正方体的一种表面展开图,那么在这个正方体的表面,与“我”相对的面上的汉字是( )
 A、爱 B、庆 C、油 D、田5. 若a,b在数轴上表示如图所示,那么( )
A、爱 B、庆 C、油 D、田5. 若a,b在数轴上表示如图所示,那么( )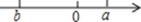 A、 B、 C、 D、6. 一次函数与反比例函数在同一坐标系内的图象可能为( )A、
A、 B、 C、 D、6. 一次函数与反比例函数在同一坐标系内的图象可能为( )A、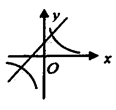 B、
B、 C、
C、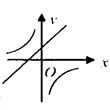 D、
D、 7. 在我县“我的中国梦”演讲比赛中,有7名同学参加了比赛,他们最终决赛的成绩各不相同.其中一名学生想要知道自己是否进入前3名,不仅要知道自己的分数,还得知道这7名学生成绩的( )A、众数 B、方差 C、平均数 D、中位数8. 寒假期间,小刚组织同学一起去看科幻电影《流浪地球》,票价每张45元,20张以上(不含20张)打八折,他们一共花了900元,则他们买到的电影票的张数是( )A、20 B、22 C、25 D、20或259. 如下图,在四边形中, , , , 点分别在边上,若 , 则 ( )
7. 在我县“我的中国梦”演讲比赛中,有7名同学参加了比赛,他们最终决赛的成绩各不相同.其中一名学生想要知道自己是否进入前3名,不仅要知道自己的分数,还得知道这7名学生成绩的( )A、众数 B、方差 C、平均数 D、中位数8. 寒假期间,小刚组织同学一起去看科幻电影《流浪地球》,票价每张45元,20张以上(不含20张)打八折,他们一共花了900元,则他们买到的电影票的张数是( )A、20 B、22 C、25 D、20或259. 如下图,在四边形中, , , , 点分别在边上,若 , 则 ( ) A、 B、 C、 D、10. 抛物线y=ax2+bx+c(a≠0)与x轴交于点(﹣3,0),其对称轴是x=﹣ , 结合图象分析下列结论:①abc>0;②a+b+c>0;③a+b=0;④2a+c>0;⑤一元二次方程ax2+bx+c=0的两根分别为x1=﹣3,x2=2;⑥>0;⑦若两点(﹣2,y1),(3,y2)在二次函数图象上,则y1>y2;其中正确的结论有( )
A、 B、 C、 D、10. 抛物线y=ax2+bx+c(a≠0)与x轴交于点(﹣3,0),其对称轴是x=﹣ , 结合图象分析下列结论:①abc>0;②a+b+c>0;③a+b=0;④2a+c>0;⑤一元二次方程ax2+bx+c=0的两根分别为x1=﹣3,x2=2;⑥>0;⑦若两点(﹣2,y1),(3,y2)在二次函数图象上,则y1>y2;其中正确的结论有( )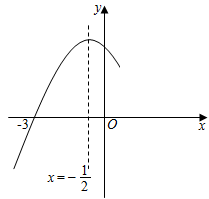 A、3个 B、4个 C、5个 D、6个
A、3个 B、4个 C、5个 D、6个二、填空题
-
11. 函数中自变量x的取值范围是.12. 如图,将一个三角板60°角的顶点与另一个三角板的直角顶点重合,∠1=27°,∠2= .
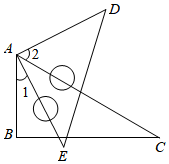 13. 圆柱的底面周长为2π,高为1,则圆柱的侧面展开图的面积为 .14. 若 则的值是 .15. 如图所示是某几何体的三视图,根据图中数据计算,这个几何体的侧面积为 .
13. 圆柱的底面周长为2π,高为1,则圆柱的侧面展开图的面积为 .14. 若 则的值是 .15. 如图所示是某几何体的三视图,根据图中数据计算,这个几何体的侧面积为 .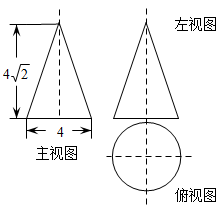 16. 若关于x的分式方程 无解,则实数m=.17. 已知实数m、n满足m2=2﹣2m,n2=2﹣2n,则= .18. 如图,在RtΔABC中,∠ACB=90°,∠ABC=60°,BC= , Q为AC上的动点,P为Rt△ABC内一动点,且满足∠APB=120°,若D为BC的中点,则PQ+DQ的最小值是 .
16. 若关于x的分式方程 无解,则实数m=.17. 已知实数m、n满足m2=2﹣2m,n2=2﹣2n,则= .18. 如图,在RtΔABC中,∠ACB=90°,∠ABC=60°,BC= , Q为AC上的动点,P为Rt△ABC内一动点,且满足∠APB=120°,若D为BC的中点,则PQ+DQ的最小值是 .
三、解答题
-
19. 计算
|-3|+(-π)0-()-1-cos30°
20. 先因式分解,再求值:4x3y﹣9xy3 , 其中x=﹣1,y=2.21. 解方程:22. 某条道路上通行车辆限速60千米/时,道路的AB段为监测区,监测点P到AB的距离PH为50米(如图).已知点P在点A的北偏东45°方向上,且在点B的北偏西60°方向上,点B在点A的北偏东75°方向上,那么车辆通过AB段的时间在多少秒以内,可认定为超速?(参考数据: ≈1.7, ≈1.4). 23. 某市制米厂接到加工大米任务,要求5天内加工完220吨大米,制米厂安排甲、乙两车间共同完成加工任务,乙车间加工中途停工一段时间维修设备,然后改变加工效率继续加工,直到与甲车间同时完成加工任务为止.设甲、乙两车间各自加工大米数量y(吨)与甲车间加工时间s(天)之间的关系如图(1)所示;未加工大米w(吨)与甲加工时间x(天)之间的关系如图(2)所示,请结合图象回答下列问题:
23. 某市制米厂接到加工大米任务,要求5天内加工完220吨大米,制米厂安排甲、乙两车间共同完成加工任务,乙车间加工中途停工一段时间维修设备,然后改变加工效率继续加工,直到与甲车间同时完成加工任务为止.设甲、乙两车间各自加工大米数量y(吨)与甲车间加工时间s(天)之间的关系如图(1)所示;未加工大米w(吨)与甲加工时间x(天)之间的关系如图(2)所示,请结合图象回答下列问题: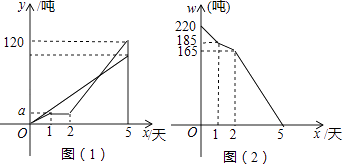 (1)、甲车间每天加工大米吨,a= .
(1)、甲车间每天加工大米吨,a= .
(2)、求乙车间维修设备后,乙车间加工大米数量y(吨)与x(天)之间函数关系式.
(3)、若55吨大米恰好装满一节车厢,那么加工多长时间装满第一节车厢?再加工多长时间恰好装满第二节车厢?24. 如图,在四边形ABCD中,对角线AC与BD交于点O,已知OA=OC,OB=OD,过点O作EF⊥BD,分别交AB、DC于点E,F,连接DE,BF,AF.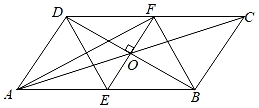 (1)、求证:四边形DEBF是菱形;(2)、设ADEF,AD+AB=12,BD=4 , 求AF的长.25. 某校开展了以“不忘初心,牢记使命”为主题的知识竞赛,现从该校八、九年级各随机抽取10名学生的成绩进行整理,描述和分析(成绩用m表示),共分成四个组:A.80≤m<85,B.85≤m<90,C.90≤m<95,D.95≤m≤100.另外给出了部分信息如下:
(1)、求证:四边形DEBF是菱形;(2)、设ADEF,AD+AB=12,BD=4 , 求AF的长.25. 某校开展了以“不忘初心,牢记使命”为主题的知识竞赛,现从该校八、九年级各随机抽取10名学生的成绩进行整理,描述和分析(成绩用m表示),共分成四个组:A.80≤m<85,B.85≤m<90,C.90≤m<95,D.95≤m≤100.另外给出了部分信息如下:八年级10名学生的成绩:99,80,99,86,99,96,90,100,89,82.
九年级10名学生的成绩在C组的数据:94,90,94.
八、九年级抽取学生成绩统计表
年级
八年级
九年级
平均数
92
92
中位数
93
b
众数
c
100
方差
52
50.4
根据以上信息,解答下列问题:
 (1)、上面图表中的a= , b= , c= .(2)、扇形统计图中“D组”所对应的圆心角的度数为 .(3)、根据以上信息,你认为哪个年级的学生对“不忘初心,牢记使命”的内容掌握较好?说明理由.(一条即可)(4)、该校九年级共有840名学生参加了知识竞赛活动,估计九年级参加此次知识竞赛活动成绩为较好(90≤m<95)的学生有多少人?26. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于一、三象限内的A,B两点,与x轴交于点C,点A的坐标为 , 点B的坐标为 , .
(1)、上面图表中的a= , b= , c= .(2)、扇形统计图中“D组”所对应的圆心角的度数为 .(3)、根据以上信息,你认为哪个年级的学生对“不忘初心,牢记使命”的内容掌握较好?说明理由.(一条即可)(4)、该校九年级共有840名学生参加了知识竞赛活动,估计九年级参加此次知识竞赛活动成绩为较好(90≤m<95)的学生有多少人?26. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于一、三象限内的A,B两点,与x轴交于点C,点A的坐标为 , 点B的坐标为 , .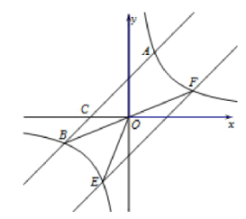 (1)、求点B的坐标及反比例函数和一次函数的表达式;(2)、将直线AB沿y轴向下平移6个单位长度后,分别与双曲线交于E,F两点,连结OE,OF,求的面积.27. 如图,△ABC内接于⊙O,AD平分∠BAC交BC边于点E,交⊙O于点D,过点A作AF⊥BC于点F,设⊙O的半径为R,AF=h.
(1)、求点B的坐标及反比例函数和一次函数的表达式;(2)、将直线AB沿y轴向下平移6个单位长度后,分别与双曲线交于E,F两点,连结OE,OF,求的面积.27. 如图,△ABC内接于⊙O,AD平分∠BAC交BC边于点E,交⊙O于点D,过点A作AF⊥BC于点F,设⊙O的半径为R,AF=h. (1)、过点D作直线MN∥BC,求证:MN是⊙O的切线;(2)、求证:AB•AC=2R•h;(3)、设∠BAC=2α,求 的值(用含α的代数式表示).28. 如图,在平面直角坐标系中,已知抛物线 与直线 相交于A,B两点,其中 , .
(1)、过点D作直线MN∥BC,求证:MN是⊙O的切线;(2)、求证:AB•AC=2R•h;(3)、设∠BAC=2α,求 的值(用含α的代数式表示).28. 如图,在平面直角坐标系中,已知抛物线 与直线 相交于A,B两点,其中 , .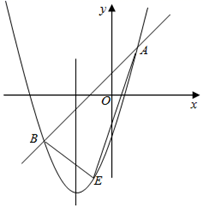 (1)、求抛物线的函数表达式;(2)、点E为直线 下方抛物线上任意一点,连接 , ,求 面积的最大值及此时点E的坐标;(3)、点D为抛物线对称轴上的一点,当以点A,B,D为顶点的三角形为等腰三角形时,直接写出点D的坐标.
(1)、求抛物线的函数表达式;(2)、点E为直线 下方抛物线上任意一点,连接 , ,求 面积的最大值及此时点E的坐标;(3)、点D为抛物线对称轴上的一点,当以点A,B,D为顶点的三角形为等腰三角形时,直接写出点D的坐标.