河北省邢台市信都区2021-2022学年九年级下学期期中数学试题(一模)
试卷更新日期:2022-04-29 类型:中考模拟
一、单选题
-
1. 如果支出30元记作﹣30元,那么收入100元记作( )A、100元 B、70元 C、﹣100元 D、﹣130元2. 下列运算正确的是( )A、a3+a2=a5 B、(ab)2=a2b2 C、a3•a2=a6 D、(a3)2=a53. 如图,为测量BC两地的距离,小明在池塘外取点A,得到线段AB,AC,并取AB,AC的中点D,E,连结DE。测得DE的长为6米,则B,C两地相距( )
 A、9米 B、10米 C、11米 D、12米4. 石墨烯是现在世界上最薄的纳米材料,其理论厍度应是0.0000098m,用科学记数法表示0.0000098是( )A、0.98×10﹣5 B、9.8×105 C、9.8×10﹣6 D、9.8×10﹣55. 下列四个图形中,属于轴对称图形的是( )A、
A、9米 B、10米 C、11米 D、12米4. 石墨烯是现在世界上最薄的纳米材料,其理论厍度应是0.0000098m,用科学记数法表示0.0000098是( )A、0.98×10﹣5 B、9.8×105 C、9.8×10﹣6 D、9.8×10﹣55. 下列四个图形中,属于轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 一组数据2,3,4,5,5,8的中位数是( )A、4 B、4.5 C、5 D、6.57. 如图,从左面看如图所示的几何体得到的平面图形是( )
6. 一组数据2,3,4,5,5,8的中位数是( )A、4 B、4.5 C、5 D、6.57. 如图,从左面看如图所示的几何体得到的平面图形是( ) A、
A、 B、
B、 C、
C、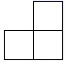 D、
D、 8. 关于反比例函数的图象性质,下列说法错误的是( )A、图象经过点 B、图象位于第一、三象限 C、当时,随的增大而增大 D、图象关于原点成中心对称9. 如图,在灯塔处观测到轮船位于灯塔南偏西15°的方向,同时观测到轮船位于灯塔北偏东50°的方向,那么的大小为( )
8. 关于反比例函数的图象性质,下列说法错误的是( )A、图象经过点 B、图象位于第一、三象限 C、当时,随的增大而增大 D、图象关于原点成中心对称9. 如图,在灯塔处观测到轮船位于灯塔南偏西15°的方向,同时观测到轮船位于灯塔北偏东50°的方向,那么的大小为( ) A、65° B、105° C、140° D、145°10. 用式子表示“比m的平方的3倍小2的数”为( )A、3m2﹣2 B、(3m)2﹣2 C、3(m﹣2)2 D、(3m﹣2)211. 将边长分别为2和4的长方形如图剪开,拼成一个正方形,则该正方形的边长最接近整数( )
A、65° B、105° C、140° D、145°10. 用式子表示“比m的平方的3倍小2的数”为( )A、3m2﹣2 B、(3m)2﹣2 C、3(m﹣2)2 D、(3m﹣2)211. 将边长分别为2和4的长方形如图剪开,拼成一个正方形,则该正方形的边长最接近整数( )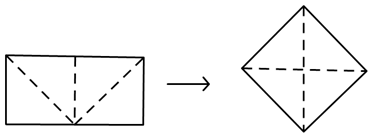 A、1 B、2 C、3 D、412. 化简的结果是( )A、a﹣1 B、a C、﹣a D、a十l13. 下列尺规作图,能确定AD=BD的是( )A、
A、1 B、2 C、3 D、412. 化简的结果是( )A、a﹣1 B、a C、﹣a D、a十l13. 下列尺规作图,能确定AD=BD的是( )A、 B、
B、 C、
C、 D、
D、 14. 如图,矩形ABCD中,AB=8cm,AD=6cm,EF是对角线BD的垂直平分线,则EF的长为( )cm.
14. 如图,矩形ABCD中,AB=8cm,AD=6cm,EF是对角线BD的垂直平分线,则EF的长为( )cm. A、 B、5 C、 D、815. 已知关于x的一元二次方程x2-kx+k+3=0,当k>6时,方程根的情况是( )A、有两个实数根 B、有两个相等的实数根 C、没有实数根 D、有两个不相等的实数根16. 有一题目:“如图,∠ABC=40°,BD平分∠ABC , 过点D作DE∥AB交BC于点E , 若点F在AB上,且满足DF=DE , 求∠DFB的度数.”小贤的解答:以D为圆心,DE长为半径画圆交AB于点F , 连接DF , 则DE=DF , 由图形的对称性可得∠DFB=∠DEB . 结合平行线的性质可求得∠DFB=140°.而小军说:“小贤考虑的不周全,∠DFB还应有另一个不同的值”.下列判断正确的是( )
A、 B、5 C、 D、815. 已知关于x的一元二次方程x2-kx+k+3=0,当k>6时,方程根的情况是( )A、有两个实数根 B、有两个相等的实数根 C、没有实数根 D、有两个不相等的实数根16. 有一题目:“如图,∠ABC=40°,BD平分∠ABC , 过点D作DE∥AB交BC于点E , 若点F在AB上,且满足DF=DE , 求∠DFB的度数.”小贤的解答:以D为圆心,DE长为半径画圆交AB于点F , 连接DF , 则DE=DF , 由图形的对称性可得∠DFB=∠DEB . 结合平行线的性质可求得∠DFB=140°.而小军说:“小贤考虑的不周全,∠DFB还应有另一个不同的值”.下列判断正确的是( ) A、小军说的对,且∠DFB的另一个值是40° B、小军说的不对,∠DFB只有140°一个值 C、小贤求的结果不对,∠DFB应该是20° D、两人都不对,∠DFB应有3个不同值
A、小军说的对,且∠DFB的另一个值是40° B、小军说的不对,∠DFB只有140°一个值 C、小贤求的结果不对,∠DFB应该是20° D、两人都不对,∠DFB应有3个不同值二、填空题
-
17. 若(a-1)2+|b-a+3|=0,则a= , b= .18. 为增强学生体质,某学校将“抖空竹”引入阳光体育一小时活动.图1是一位同学抖空竹时的一个瞬间,数学老师把它抽象成图2的数学问题:已知AB∥CD,∠EAB=80°,∠ECD=110°.求∠AEC的度数.小明在解决过程中,过E点作EF∥CD,则可以得到EF∥AB,其理由是 , 根据这个思路可得∠AEC=°.
 19. 如图,在边长为2的正六边形ABCDEF内,以CD为边作正方形CDGT;
19. 如图,在边长为2的正六边形ABCDEF内,以CD为边作正方形CDGT; (1)、∠BCT=°;(2)、连接BT、GE,则六边形BCDEGT的面积为 .
(1)、∠BCT=°;(2)、连接BT、GE,则六边形BCDEGT的面积为 .三、解答题
-
20. 已知数轴上点A,B,C所表示的数分别是4,﹣6,x.(1)、求线段AB的长;(2)、若点A与点C关于点B对称,求x的值.21. 老师写出一个整式(ax2+bx﹣1)﹣(4x2+3x)(其中a,b为常数),然后让同学们给a,b赋予不同的数值进行化简.(1)、甲同学给出了a=5,b=﹣1,请按照甲同学给出的数值化简整式;(2)、乙同学给出了一组数据,最后化简的结果为2x2﹣3x﹣1,求a,b的值.22. 某校测量了九年级同学的身高(单位:cm),根据测量数据绘制了如下两幅不完整的统计图,请结合图中提供的信息,解答下列问题.
 (1)、填空:样本容量为 , a= .(2)、把频数分布直方图补充完整;(3)、随机抽取该校九年级的1名学生,估计这名学生身高不低于165cm的概率.23. 如图所示,已知AB=AC,CB平分∠ACD,CD=CA,E是BC上一点,连接DE并延长交AB于F.
(1)、填空:样本容量为 , a= .(2)、把频数分布直方图补充完整;(3)、随机抽取该校九年级的1名学生,估计这名学生身高不低于165cm的概率.23. 如图所示,已知AB=AC,CB平分∠ACD,CD=CA,E是BC上一点,连接DE并延长交AB于F.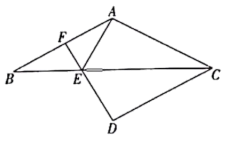 (1)、求证:AEC≌DEC;(2)、连接BD,求证四边形ABDC是菱形;(3)、若F是AB的中点,EF=3,求AE的长.24. 某家电商店计划购进并销售甲、乙两种品牌小家电,已知甲品牌家电每台进价为200元,售价为280元,乙品牌家电每台进价为400元,售价为500元,若该家电商店购进甲品牌家电x台,乙品牌家电y台,恰好花费20000元.(1)、求y与x之间的函数关系式;(2)、已知购买两种家电的总台数不超过60台,全部售完这些家电所获得的总利润为W元,求当为何值时,W最大,最大值是多少.25. 如图所示,已知∠OAB=45°,OA=10,BA=10 , AO⊥CD于O,以CD为直径作半圆O,且CD=10,将线段BA绕点A顺时针旋转得到线段AB'.
(1)、求证:AEC≌DEC;(2)、连接BD,求证四边形ABDC是菱形;(3)、若F是AB的中点,EF=3,求AE的长.24. 某家电商店计划购进并销售甲、乙两种品牌小家电,已知甲品牌家电每台进价为200元,售价为280元,乙品牌家电每台进价为400元,售价为500元,若该家电商店购进甲品牌家电x台,乙品牌家电y台,恰好花费20000元.(1)、求y与x之间的函数关系式;(2)、已知购买两种家电的总台数不超过60台,全部售完这些家电所获得的总利润为W元,求当为何值时,W最大,最大值是多少.25. 如图所示,已知∠OAB=45°,OA=10,BA=10 , AO⊥CD于O,以CD为直径作半圆O,且CD=10,将线段BA绕点A顺时针旋转得到线段AB'. (1)、若点M是半圆O上一点,则BM的最大值为;(2)、当经过点C时,设与半圆O的另一个交点为E,求AE的长;(3)、当与半圆O相切时,设切点为N,求长.26. 如图所示,在平面直角坐标系中,抛物线L:y=x2bx+c与直线l1:y=﹣x+1交于点A,且点A的横坐标为﹣4,设抛物线的顶点为M,点N(0,n)是y轴上一点,过点N作直线l2x轴.
(1)、若点M是半圆O上一点,则BM的最大值为;(2)、当经过点C时,设与半圆O的另一个交点为E,求AE的长;(3)、当与半圆O相切时,设切点为N,求长.26. 如图所示,在平面直角坐标系中,抛物线L:y=x2bx+c与直线l1:y=﹣x+1交于点A,且点A的横坐标为﹣4,设抛物线的顶点为M,点N(0,n)是y轴上一点,过点N作直线l2x轴. (1)、请用含b的代数式表示c;(2)、若直线l2在点M的上方,且点M到直线l2的距离为2,求n的最大值;(3)、若点B在直线l1上,且点B的横坐标为﹣2,点C( , 3),若抛物线L与线段BC有公共点,结合图像,直接写出b的取值范围.
(1)、请用含b的代数式表示c;(2)、若直线l2在点M的上方,且点M到直线l2的距离为2,求n的最大值;(3)、若点B在直线l1上,且点B的横坐标为﹣2,点C( , 3),若抛物线L与线段BC有公共点,结合图像,直接写出b的取值范围.