安徽省宿州市泗县2021-2022学年九年级下学期期中数学试题(一模)
试卷更新日期:2022-04-29 类型:中考模拟
一、单选题
-
1. -2的相反数是( )A、2 B、-2 C、 D、2. 第七次全国人口普查数据显示,全国人口共141178万人,比第六次人口普查增加7206万人.数据“7206万”用科学记数法表示正确的是( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 一个正方形的面积是20,通过估算,它的边长在整数与之间,则的值是( )A、3 B、4 C、5 D、65. 如图,直线 , 将一个三角板的直角顶点放在直线上,若 , 则的度数是( )
 A、 B、 C、 D、6. 据统计,某班7个学习小组上周参加“青年大学习”的人数分别为5,6,7,6,5,6,7.下列说法正确的是( )A、该组数据的中位数是6 B、该组数据的众数是7 C、该组数据的平均数是6.5 D、该组数据的方差是67. 在平面直角坐标系中,若将一次函数的图象向左平移3个单位后,得到一个正比例函数的图象,则m的值为( )A、-5 B、5 C、-6 D、68. 若方程 没有实数根,则 的值可以是( )A、-1 B、 C、1 D、9. 已知 为实数,且满足 ,当a-b为整数时,ab的值为( )A、 或 B、 或1 C、 或1 D、 或10. 如图,在矩形中, , , 点在上,点在上,且 , 连接 , , 则的最小值为( )
A、 B、 C、 D、6. 据统计,某班7个学习小组上周参加“青年大学习”的人数分别为5,6,7,6,5,6,7.下列说法正确的是( )A、该组数据的中位数是6 B、该组数据的众数是7 C、该组数据的平均数是6.5 D、该组数据的方差是67. 在平面直角坐标系中,若将一次函数的图象向左平移3个单位后,得到一个正比例函数的图象,则m的值为( )A、-5 B、5 C、-6 D、68. 若方程 没有实数根,则 的值可以是( )A、-1 B、 C、1 D、9. 已知 为实数,且满足 ,当a-b为整数时,ab的值为( )A、 或 B、 或1 C、 或1 D、 或10. 如图,在矩形中, , , 点在上,点在上,且 , 连接 , , 则的最小值为( ) A、25 B、24 C、 D、13
A、25 B、24 C、 D、13二、填空题
-
11. 计算: .12. 如图,内接于⊙O, , 则⊙O的直径等于 .
 13. 疫情期间,泗县各校都设置测温通道,体温正常才可进入学校,泗县某校有2个测温通道,学生可随机选取其中的一个通道测温进入校园.某日早晨小王和小李两同学进校园时,选择同一通道测温进校园的概率是 .14. 在平在直角坐标系中,已知抛物线 (a是常数,且 ),直线 过点 且垂直于y轴.(1)、该抛物线顶点的纵坐标为 (用含a的代数式表示);(2)、当 时,沿直线 将该抛物线在直线上方的部分翻折,其余部分不变,得到新图象G,图象G对应的函数记为 ,且当 时,函数 的最大值与最小值之差小于7,则n的取值范围为: .
13. 疫情期间,泗县各校都设置测温通道,体温正常才可进入学校,泗县某校有2个测温通道,学生可随机选取其中的一个通道测温进入校园.某日早晨小王和小李两同学进校园时,选择同一通道测温进校园的概率是 .14. 在平在直角坐标系中,已知抛物线 (a是常数,且 ),直线 过点 且垂直于y轴.(1)、该抛物线顶点的纵坐标为 (用含a的代数式表示);(2)、当 时,沿直线 将该抛物线在直线上方的部分翻折,其余部分不变,得到新图象G,图象G对应的函数记为 ,且当 时,函数 的最大值与最小值之差小于7,则n的取值范围为: .三、解答题
-
15. 解不等式组:并在数轴上表示它的解集.
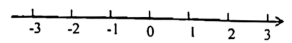 16. 如图,在中,∠B=90°, , 若AB=10,求BC的长.
16. 如图,在中,∠B=90°, , 若AB=10,求BC的长. 17. 《九章算术》中有一道阐述“盈不足术”的问题,原文如下:
17. 《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出八,盈三;人出七,不足四.问人数,物价各几何?
译文为:
现有一些人共同买一个物品,每人出8元,还盈余3元;每人出7元,则还差4元,问共有多少人?这个物品的价格是多少?
请解答上述问题.
18. 观察以下等式:第1个等式:22﹣12=2×1+1,
第2个等式:32﹣22=2×2+1,
第3个等式:42﹣32=2×3+1,
第4个等式:52﹣42=2×4+1,
…
按照以上规律,解决下列问题:
(1)、写出第5个等式: .(2)、写出你猜想的第n个等式: ▲ (用含n的等式表示),并证明.19. 在平面直角坐标系中,一次函数和反比例函数的图象都经过点 , . (1)、求的值和一次函数的表达式;(2)、不等式的解集是 .20. 由中宣部建设的“学习强国”学习平台正式上线,这是推动习近平新时代中国特色社会主义思想,推进马克思主义学习型政党和学习型社会建设的创新举措.某基层党组织对党员的某天的学习成绩进行了整理,分成5个小组(表示成绩,单位:分,且),根据学习积分绘制出部分频数分布表和部分频数分布直方图,其中第2、第5两组测试成绩人数直方图的高度比为4:1,请结合下列图表中相关数据回答下列问题:
(1)、求的值和一次函数的表达式;(2)、不等式的解集是 .20. 由中宣部建设的“学习强国”学习平台正式上线,这是推动习近平新时代中国特色社会主义思想,推进马克思主义学习型政党和学习型社会建设的创新举措.某基层党组织对党员的某天的学习成绩进行了整理,分成5个小组(表示成绩,单位:分,且),根据学习积分绘制出部分频数分布表和部分频数分布直方图,其中第2、第5两组测试成绩人数直方图的高度比为4:1,请结合下列图表中相关数据回答下列问题:学习积分频数分布表
组别
成绩分
频数
频率
第1组
5
第2组
第3组
15
30%
第4组
10
第5组
 (1)、填空: , ;(2)、补全频数分布直方图:(3)、已知该基层党组织中甲、乙两位党员的学习积分分别为61分、65分,现在从第5组中随机选取2人介绍经验,请用列表法或画树状图的方法,求出甲、乙两人中只有1人被选中的概率.21. 如图,是半圆的直径,、是半圆上不同于、的两点,与相交于点 , 是半圆所在圆的切线,与的延长线相交于点 .
(1)、填空: , ;(2)、补全频数分布直方图:(3)、已知该基层党组织中甲、乙两位党员的学习积分分别为61分、65分,现在从第5组中随机选取2人介绍经验,请用列表法或画树状图的方法,求出甲、乙两人中只有1人被选中的概率.21. 如图,是半圆的直径,、是半圆上不同于、的两点,与相交于点 , 是半圆所在圆的切线,与的延长线相交于点 . (1)、若 , 证明:;(2)、若 , , 求的度数.
(1)、若 , 证明:;(2)、若 , , 求的度数.

