云南省昆明市西山区2022年初中学业水平第一次模拟考试数学试题

试卷更新日期：2022-04-29 类型：中考模拟

进入出卷网下载

一、单选题

1. －5的相反数是（）

A、 $- \frac{1}{5}$ B、 $\frac{1}{5}$ C、5 D、-5

查看试题解析
2. 图中三棱柱的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 下表记录了一名球员在罚球线上投篮的结果．
投篮次数n
50
100
150
200
250
300
500
1000
投中次数m
28
60
78
104
123
152
251
502
投中频率（精确到0.01）
0.56
0.60
0.52
0.52
0.49
0.51
0.50
0.50
由此估计这名球员在罚球线上投中篮的概率约是（）（精确到0.01）

A、0.50 B、0.51 C、0.49 D、0.52

查看试题解析
4. 如图，直线 $a ∥ b$ ，若∠1＝52°，则∠2的度数为（）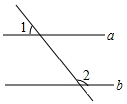

A、152° B、138° C、128° D、142°

查看试题解析
5. 下列计算正确的是（）

A、 $\sqrt{9} = \pm 3$ B、 $(- 4)^{- 2} = 16$ C、 $(- 3 x y) \div \frac{2 y^{2}}{3 x} = - 2 y^{3}$ D、 $(- x + 2 y) (- x - 2 y) = x^{2} - 4 y^{2}$

查看试题解析
6. 一元二次方程 $2 x^{2} - 3 x - 1 = 0$ 的根的情况是（）

A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法判断

查看试题解析
7. 围棋起源于中国，古代称之为“弈”，至今已有4000多年的历史．如图，黑白棋子摆成的图案里下一黑棋，黑棋落在（）号位置上使棋子构成的图形既是轴对称图形也是中心对称图形．

A、1 B、2 C、3 D、4

查看试题解析
8. 如图，AB是 $⊙ O$ 的直径，点C在 $⊙ O$ 上，半径 $O D ⊥ A C$ ，连接BD，AD，若∠ABD＝27°，则∠BAC是（）

A、27° B、36° C、53° D、54°

查看试题解析
9. 观察下面的一列单项式： $- x$ ， $2 x^{2}$ ， $- 4 x^{3}$ ， $8 x^{4}$ ， $- 16 x^{5}$ ， …根据其中的规律，得出的第2022个单项式是（）

A、 $2^{2021} x^{2022}$ B、 $- 2^{2021} x^{2022}$ C、 $2^{2022} x^{2022}$ D、 $- 2^{2022} x^{2022}$

查看试题解析
10. 在同一平面直角坐标系中，函数 $y = k x^{2} - k (k \neq 0)$ 与 $y = \frac{k}{x} (k \neq 0)$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
11. 如图，从一块半径为2m的圆形铁皮上剪出一个扇形ABC，且 $\overset{⌢}{B C}$ 经过圆心O．如果将剪下来的扇形围成一个圆锥，则该圆锥的底面圆的半径为（）m

A、2 B、1 C、 $\frac{2}{3}$ D、 $\frac{1}{2}$

查看试题解析
12. 关于x的不等式组 ${\begin{array}{l} \frac{2 x + 1}{3} \geq x - 1 \\ 2 x > a + 1 \end{array}$ 有且只有2个奇数解，则符合条件的所有整数a的和为（）

A、－6 B、－3 C、0 D、6

查看试题解析

二、填空题

13. 若 $\sqrt{x + 3}$ 有意义，则 $x$ 的取值范围是.

查看试题解析
14. 点 $A (4 ， 1)$ 关于x轴的对称点B的坐标是．

查看试题解析
15. 点A（x₁ ， y₁），B（x₂ ， y₂）是反比例函数 $y = \frac{1}{x}$ 的图象上两点，若0＜x₁＜x₂ ，则y₁、y₂的大小关系是．

查看试题解析
16. 当 $m = 2 n - 3$ 时，代数式 $m^{2} - 4 m n + 4 n^{2} =$ ．

查看试题解析
17. 数学兴趣小组利用无人机测量学校旗杆高度，无人机的飞行高度为27米，无人机与旗杆的水平距离是30米时，观测旗杆顶部的俯角为30°，则旗杆的高度约为米．（结果精确到1米，参考数据： $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73$ ）

查看试题解析
18. 如图，五边形DEFGH是边长为1的正五边形， $⊙ O$ 是正五边形DEFGH的外接圆，过点D作 $⊙ O$ 的切线，与GH，FE的延长线交分别于点B和C，延长HG，EF相交于点A，连接GD，DF，下列结论：①∠HDE＝108°；②△ABC为等腰三角形；③四边形AGDF为菱形；④△ABC的周长为 $2 \sqrt{5} + 2$ ．正确的是．

查看试题解析

三、解答题

19. 某校在“庆祝建党100周年”系列活动中举行了主题为“学史明理，学史增信，学史崇德，学史力行”的党史知识竞赛．九年级某班“班级党史知识竞赛”中，有A，B，C，D四名同学的竞赛成绩为满分．

(1)、若该班要随机从4名满分同学中选取1名同学参加学校的党史知识竞赛，A同学被选中的概率是．

(2)、该班4位满分同学中A和B是女生，C和D是男生，若要从4名满分同学中随机抽取两名同学参加学校的党史知识竞赛，请用画树状图或列表的方法求出抽到两名女生的概率．

查看试题解析
20. 2022年北京冬季奥运会，于2022年2月4日至2022年2月20日在北京市和河北省张家口市联合举行，中国代表团取得九金四银两铜的好成绩，第一次进入奖牌榜前三名．时隔十三年，北京再度点燃奥林匹克圣火，首次举办冬奥会，成为首个“双奥城”．近四届冬奥会的投资规模北京冬奥会最少，约39亿美元．各项预算投入资金分配如扇形统计图所示．综合考虑中国国情、冬奥会特点等因素，2022年冬奥会开闭幕式的门票为118－787美元，相比过往几届冬奥会，2022年冬奥会门票价格相对较低.2006－2022年四届冬奥会开、闭幕式门票价格如条形统计图所示．

(1)、在扇形统计图中表示其他投入资金的扇形所占的圆心角为度，比赛场馆建设资金分配约美元．（用科学记数法表示）

(2)、求2006－2022年四届冬奥会开、闭幕式门票最高票价的平均值和最低票价的中位数．

查看试题解析
21. 接种疫苗是阻断新冠病毒传播的有效途经，保障人民群众的身体健康．据某市3月份统计，甲接种点完成一批加强针的接种任务用了m天，乙接种点完成相同数量的加强针接种任务多用2天，且乙接种点平均每天接种加强针的人数比甲接种点少20%．

(1)、求整数m的值．

(2)、接种工作包含登记、接种、留观，需要组队完成．某中学现有2160人符合接种加强针条件，甲接种点需要组建A和B两种团队到校接种，A种团队每小时可完成100人的接种，B种团队每小时可完成60人的接种．若AB两种团队共10个，其中A种团队不超过5个，要求上午9点同时开始工作，中午12点前（包含12点）完成．问甲接种点有几种派遣方案前往该中学可以在12点前（包含12点）完成该校加强针的接种．

查看试题解析
22. 我们学习过利用尺规作图平分一个任意角，而“利用尺规作图三等分一个任意角”曾是数学史上一大难题，之后被数学家证明是不可能完成的．人们根据实际需要，发明了一种简易操作工具—“三分角器”．图1是它的示意图，其中如与半圆O的直径BC在同一直线上，且AB的长度与半圆的半径相等；DB与AC垂直于点B，DB足够长．使用方法如图2所示，若要把∠MEN三等分，只需适当放置三分角器，使DB经过∠MEN的顶点E，点A落在边EM上，半圆O与另一边EN恰好相切，切点为F，则EB，EO就把∠MEN三等分了．为了说明这一方法的正确性，需要对其进行证明．如下给出了不完整的“已知”和“求证”，请补充完整，并写出“证明”过程．
已知：如图2，点A，B，O，C在同一直线上， $E B ⊥ A C$ ，垂足为点B，半圆O与EN相切于点F，........... ．

求证：EB，EO是∠MEN三等分线．

查看试题解析
23. 如图，平面直角坐标系中，O是坐标原点，直线 $y = k x + 15 (k \neq 0)$ 经过点 $C (3 ， 6)$ ，与x轴交于点A，y轴交于点B，线段CD平行于x轴，交直线 $y = \frac{3}{4} x$ 于点D，连接OC，AD．

(1)、求证：四边形OADC是平行四边形；

(2)、动点P从点O出发，沿对角线OD以每秒1个单位长度的速度向点D运动，直到点D为止；动点Q同时从点D出发，沿对角线DO以每秒1个单位长度的速度向点O运动，直到点O为止．设两个点的运动时间均为t秒．当点P，Q运动至四边形CPAQ矩形时，请求此时t的值．

查看试题解析
24. 抛物线与x轴交于A，B两点，与y轴交于点C，已知点 $A (- 3 ， 0)$ ，抛物线的最低点的坐标为 $(- 1 ， - 4)$ ．

(1)、求出该抛物线的函数解析式；

(2)、如图1，线段BC绕点C逆时针旋转90°得到线段CD线段，CD与抛物线相交于点E，求点E的坐标．

(3)、如图2，点M，N是线段AC上的动点，且 $M N = \sqrt{2}$ ，求△OMN周长的最小值．

查看试题解析

投篮次数n	50	100	150	200	250	300	500	1000
投中次数m	28	60	78	104	123	152	251	502
投中频率（精确到0.01）	0.56	0.60	0.52	0.52	0.49	0.51	0.50	0.50