云南省昆明市官渡区2022年初中学业水平考试第一次模拟测试数学试题
试卷更新日期:2022-04-29 类型:中考模拟
一、单选题
-
1. 四个大小相同的小正方体拼成如图所示的几何体,则这个几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 如图,直线、被直线l所截,// , , 则的度数是( )
2. 如图,直线、被直线l所截,// , , 则的度数是( ) A、44° B、46° C、134° D、136°3. 已知反比例函数上的图象经过点 , 则k的值是( )A、-3 B、3 C、 D、4. 不等式组的解集在数轴上表示正确的是( )A、
A、44° B、46° C、134° D、136°3. 已知反比例函数上的图象经过点 , 则k的值是( )A、-3 B、3 C、 D、4. 不等式组的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、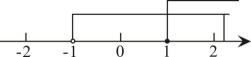 5. 下列计算正确的是( )A、 B、 C、 D、6. 如图, , , 是五边形的3个外角,若 , 则等于( )
5. 下列计算正确的是( )A、 B、 C、 D、6. 如图, , , 是五边形的3个外角,若 , 则等于( ) A、130° B、180° C、230° D、330°7. 关于x的一元二次方程有实数根,则k的取值范围是( )A、 B、且 C、 D、且8. 如图,小明在数学兴趣小组探究活动中要测量河的宽度,他和同学在河对岸选定一点A,再在河的这一边选定点P和点B,使 . 利用工具测得米, , 根据测量数据可计算得到小河宽度为( )
A、130° B、180° C、230° D、330°7. 关于x的一元二次方程有实数根,则k的取值范围是( )A、 B、且 C、 D、且8. 如图,小明在数学兴趣小组探究活动中要测量河的宽度,他和同学在河对岸选定一点A,再在河的这一边选定点P和点B,使 . 利用工具测得米, , 根据测量数据可计算得到小河宽度为( ) A、米 B、米 C、米 D、米9. 按一定规律排列的单项式:a, , , , , , …,第2022个单项式是( )A、 B、 C、 D、10. 当今,大数据、云计算、人工智能等互联网新技术正在全方位改写中国社会,而应用将是推动互联网这个“最大变量”变成“最大增量”的新引擎,的出现将改变中国的经济格局,据预测,2020年到2030年中国直接经济产出和间接经济产出的情况如图所示,根据图提供的信息,下列推断不合理的是( )
A、米 B、米 C、米 D、米9. 按一定规律排列的单项式:a, , , , , , …,第2022个单项式是( )A、 B、 C、 D、10. 当今,大数据、云计算、人工智能等互联网新技术正在全方位改写中国社会,而应用将是推动互联网这个“最大变量”变成“最大增量”的新引擎,的出现将改变中国的经济格局,据预测,2020年到2030年中国直接经济产出和间接经济产出的情况如图所示,根据图提供的信息,下列推断不合理的是( ) A、2022年间接经济产出比直接经济产出多2万亿元 B、2026年直接经济产出为2021年直接经济产出的4倍 C、2020年到2030年,直接经济产出和间接经济产出都是逐年增长 D、2023年到2024年与2028年到2029年间接经济产出的增长率相同11. 古希腊时期,人们认为最美人体的肚脐至脚底的长度与身高长度之比约为0.618,著名的“断臂维纳斯”便是如此.若王老师身高 , 肚脐到脚底的长度为 , 为使王老师穿上高跟鞋以后更接近最美人体比例,选择高跟鞋的跟高约为( )A、 B、 C、 D、12. 在平行四边形中, , , , 点E是边上的动点,过点B作直线的垂线,垂足为F,当点E从点A运动到点B时,点F的运动路径长为( )
A、2022年间接经济产出比直接经济产出多2万亿元 B、2026年直接经济产出为2021年直接经济产出的4倍 C、2020年到2030年,直接经济产出和间接经济产出都是逐年增长 D、2023年到2024年与2028年到2029年间接经济产出的增长率相同11. 古希腊时期,人们认为最美人体的肚脐至脚底的长度与身高长度之比约为0.618,著名的“断臂维纳斯”便是如此.若王老师身高 , 肚脐到脚底的长度为 , 为使王老师穿上高跟鞋以后更接近最美人体比例,选择高跟鞋的跟高约为( )A、 B、 C、 D、12. 在平行四边形中, , , , 点E是边上的动点,过点B作直线的垂线,垂足为F,当点E从点A运动到点B时,点F的运动路径长为( ) A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
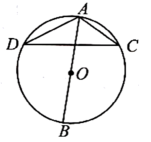
13. 若二次根式在实数范围内有意义,则x的取值范围是 .14. 若 , 则 .15. 计算: .16. 如图,为的外接圆的直径,若 , 则的度数为°.
 17. 如图,正六边形的边长为4,以A为圆心,的长为半径画弧,得 , 连接 , , 则图中阴影部分的面积为 .
17. 如图,正六边形的边长为4,以A为圆心,的长为半径画弧,得 , 连接 , , 则图中阴影部分的面积为 . 18. 已知二次函数 , 当时有最小值5,则a的值为 .
18. 已知二次函数 , 当时有最小值5,则a的值为 .三、解答题
-
19. 为培养学生良好的运动习惯,提高学生的身体素质,我校开展了“花样跳绳”和“春季长跑”等体育活动.体育老师随机抽取了八年级男、女各60名学生的长跑成绩,并将数据进行整理分析,给出了下面部分信息:
数据分为A,B,C,D四个等级,分别是:
A: , B: , C: , D:
60名男生成绩的条形统计图以及60名女生成绩的扇形统计图如图:

男生成绩位于B等级前10名的分数为:
95,95,95,94,94,94,92,91,90,90.
60名男生和60名女生成绩的平均数,中位数,众数如下表:
性别
平均数
中位数
众数
男生
94
a
96
女生
95
94
96
根据以上信息,解答下列问题:
(1)、填空: , ;(2)、计算抽取的男生成绩在B等级的人数,并补全条形统计图;(3)、根据以上数据,你认为在此次活动中,男生成绩好还是女生成绩好?请说明理由(说明一条理由即可).(4)、若该年级有800名学生,估计成绩为A等级的学生约为人.20. 如图,有4张背面相同的纸牌A,B,C,D正面分别写着四个不同的数字. (1)、求摸出一张纸牌恰好是负数的概率是;(2)、将这4张纸牌背面朝上洗匀后摸出一张,不放回,然后再摸出一张.求摸出两张牌面数字恰好一个是有理数,一个是无理数的概率.(用树状图或列表法求解,纸牌可用A,B,C,D表示)21. 学习函数时,我们经历了“确定函数解析式、画出函数图象、利用函数图象研究函数性质、利用函数性质解决问题”的学习过程.以下是我们研究函数的图象和性质的部分过程,请按要求完成下列问题.(1)、列表:y与x的部分对应值如下表,则 , ;
(1)、求摸出一张纸牌恰好是负数的概率是;(2)、将这4张纸牌背面朝上洗匀后摸出一张,不放回,然后再摸出一张.求摸出两张牌面数字恰好一个是有理数,一个是无理数的概率.(用树状图或列表法求解,纸牌可用A,B,C,D表示)21. 学习函数时,我们经历了“确定函数解析式、画出函数图象、利用函数图象研究函数性质、利用函数性质解决问题”的学习过程.以下是我们研究函数的图象和性质的部分过程,请按要求完成下列问题.(1)、列表:y与x的部分对应值如下表,则 , ;x
…
-3
-2
-1
0
1
2
3
…
y
…
m
0
1
2
1
n
…
(2)、描点、连线:根据上表中的数据,在平面直角坐标系中画出函数的图象; (3)、结合图象,写一条函数的性质:;(4)、根据函数图象填空:
(3)、结合图象,写一条函数的性质:;(4)、根据函数图象填空:①方程有个解;
②若关于x的方程无解,则a的取值范围是 .
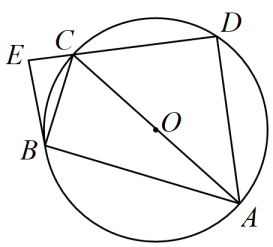
22. 如图,是四边形的外接圆,是的直径, , 交的延长线于点E,平分 .\
 (1)、求证:是的切线;(2)、若 , , 求的长.23. 2022年北京冬奥会即将召开,激起了人们对冰雪运动的极大热情.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为 轴,过跳台终点 作水平线的垂线为 轴,建立平面直角坐标系.图中的抛物线 近似表示滑雪场地上的一座小山坡,某运动员从点 正上方 米处的 点滑出,滑出后沿一段抛物线 运动.
(1)、求证:是的切线;(2)、若 , , 求的长.23. 2022年北京冬奥会即将召开,激起了人们对冰雪运动的极大热情.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为 轴,过跳台终点 作水平线的垂线为 轴,建立平面直角坐标系.图中的抛物线 近似表示滑雪场地上的一座小山坡,某运动员从点 正上方 米处的 点滑出,滑出后沿一段抛物线 运动.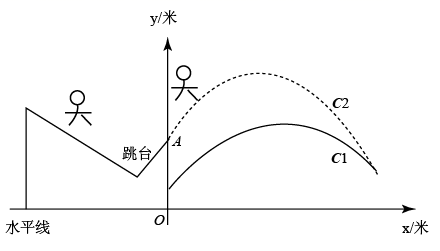 (1)、当运动员运动到离 处的水平距离为4米时,离水平线的高度为8米,求抛物线 的函数解析式(不要求写出自变量 的取值范围);(2)、在(1)的条件下,当运动员运动水平线的水平距离为多少米时,运动员与小山坡的竖直距离为1米?(3)、当运动员运动到坡顶正上方,且与坡顶距离超过3米时,求 的取值范围.24. 矩形中,、交于点O,(k为常数).作 , 、分别与、边相交于点E、F,连接 ,
(1)、当运动员运动到离 处的水平距离为4米时,离水平线的高度为8米,求抛物线 的函数解析式(不要求写出自变量 的取值范围);(2)、在(1)的条件下,当运动员运动水平线的水平距离为多少米时,运动员与小山坡的竖直距离为1米?(3)、当运动员运动到坡顶正上方,且与坡顶距离超过3米时,求 的取值范围.24. 矩形中,、交于点O,(k为常数).作 , 、分别与、边相交于点E、F,连接 , (1)、发现问题:如图1,若 , 猜想:;(2)、类比探究:如图2, , 探究线段 , 之间的数量关系,并说明理由;(3)、拓展运用:如图3,在(2)的条件下,若 , , , 求的长.
(1)、发现问题:如图1,若 , 猜想:;(2)、类比探究:如图2, , 探究线段 , 之间的数量关系,并说明理由;(3)、拓展运用:如图3,在(2)的条件下,若 , , , 求的长.