云南省保山市隆阳区2022年中考模拟数学试题（一）

试卷更新日期：2022-04-29 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图，点A表示的数是﹣3，则点A到原点的距离是（）

A、3 B、﹣3 C、±3 D、0

查看试题解析
2. 如图，AB∥CD，∠AEC＝70°、∠C＝30°，则∠A的度数为（）

A、30° B、35° C、40° D、45°

查看试题解析
3. 已知反比例函数 $y = \frac{k}{x}$ 的图象经过点（2，﹣5），则k的值为（）

A、﹣10 B、10 C、﹣7 D、7

查看试题解析
4. 下列几何体的三视图相同的是（）

A、 B、 C、 D、

查看试题解析
5. 不等式组 ${\begin{array}{l} x + 1 > 0 \\ 4 x - 8 ⩽ 0 \end{array}$ 的解集在数轴上表示，正确的是（）

A、 B、 C、 D、

查看试题解析
6. 下列判断正确的是（）

A、一组数据6，5，8，7，9的中位数是8 B、“三角形的内角和为180°”是必然事件 C、甲、乙两组学生身高的方差分别为S_甲²＝1.6，S_乙²＝0.8，则甲组学生的身高较整齐 D、神舟十三号卫星发射前的零件检查，应选择抽样调查

查看试题解析
7. 如图，四边形 $A B C D$ 是菱形，点E，F分别在 $B C ， D C$ 边上，添加以下条件不能判定 $△ A B E ≌ △ A D F$ 的是（）

A、 $B E = D F$ B、 $∠ B A E = ∠ D A F$ C、 $A E = A D$ D、 $∠ A E B = ∠ A F D$

查看试题解析
8. 下列运算正确的是（）

A、 $\sqrt{9} = \pm 3$ B、 $202 2^{0} - (- \frac{1}{2})^{- 2} = - 3$ C、（a+b）²＝a²+b² D、（﹣4a³b）²＝16a⁶b

查看试题解析
9. 若m是一元二次方程x²﹣3x﹣1＝0的根，则2m²﹣6m+2020的值是（）

A、2018 B、2021 C、2022 D、2023

查看试题解析
10. 如图，在 $4 \times 5$ 的正方形网格中，每个小正方形的边长都是1， $△ A B C$ 的顶点都在这些小正方形的顶点上，那么 $\sin ∠ A C B$ 的值为（）．

A、 $\frac{3 \sqrt{5}}{5}$ B、 $\frac{\sqrt{17}}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
11. 如图，正六边形ABCDEF的边长为6，以顶点A为圆心，AB的长为半径画弧，则由图中阴影部分的扇形围成的圆锥的高为（）

A、 $4 \sqrt{2}$ B、 $2 \sqrt{6}$ C、 $3 \sqrt{3}$ D、4

查看试题解析
12. 数学兴趣小组在讨论求1+2+2²+2³+2⁴+2⁵+2⁶+2⁷+2⁸的值时，成员小云发现：从第二个加数起每一个加数都是前一个加数的2倍，于是他假设：S＝1+2+2²+2³+2⁴+2⁵+2⁶+2⁷+2⁸①，然后在①式的两边都乘以2，得：2S＝2+2²+2³+2⁴+2⁵+2⁶+2⁷+2⁸+2⁹②，②﹣①得：2S﹣S＝2⁹﹣1，所以S＝2⁹﹣1．得出答案后，爱动脑筋的小云想：如果把“2”换成字母a（a≠0且a≠1），能否求出1+a+a²+a³+a⁴+…+a²⁰²²的值？最后通过小组共同努力求出正确答案是（）

A、a²⁰²²﹣1 B、a²⁰²³﹣1 C、 $\frac{a^{2022} - 1}{a - 1}$ D、 $\frac{a^{2023} - 1}{a - 1}$

查看试题解析

二、填空题

13. 要使式子 $\sqrt{2 - x}$ 有意义，则x的取值范围是．

查看试题解析
14. 如图，AB是⊙O的直径，点C，D在圆上，∠ACD＝55°，则∠BAD的度数为．

查看试题解析
15. 化简 $\frac{x - 6}{x^{2} - 4} - \frac{1}{2 - x} =$ ．

查看试题解析
16. 如图，点D为Rt△ABC斜边AB的中点，点E为边AC上一点，EF∥CD交AB于F，若AB＝8， $\frac{A E}{E C} = \frac{3}{2}$ ，则EF的长为．

查看试题解析
17. 如图，二次函数y＝ax²+bx+c的图象经过点A（﹣3，0），B（1，0），与y轴交于点C．下列结论：①abc＞0；②3a﹣c＝0；③当x＜0时，y随x的增大而增大；④对于任意实数m，总有a﹣b≥am²﹣bm．其中正确的是（填写序号）．

查看试题解析
18. 若点O是等腰△ABC的外心，且∠BOC＝40°，则△ABC的底角的度数为 °．

查看试题解析

三、解答题

19. 某校举行了“风雨百年路，青春心向党”知识竞赛，现从七、八年级中各随机抽取20名学生的测试成绩（满分10分，8分及以上为优秀）进行整理和分析如下：
七年级20名学生的测试成绩为：
7，8，7，8，7，5，5，9，10，9，7，5，8，7，7，7，9，8，10，7
八年级20名学生的测试成绩如下：
两个年级分析数据如表：
年级
平均数
众数
中位数
6分以上人数百分比
七年级
7.5
7
b
c
八年级
7.5
a
7.5
90%
根据以上信息，解答下列问题：

(1)、a＝， b＝， c＝；

(2)、如果八年级参加测试有500名学生，估计成绩为优秀的学生人数有多少人？

(3)、根据以上数据，你认为七、八年级中哪个年级学生测试成绩较好？请说理由．

查看试题解析
20. 如图，有四张正面标有数字﹣2，﹣1，0，1，背面颜色一样的卡片，正面朝下放在桌面上，小红从四张卡片中随机抽取一张卡片记下数字，小明再从余下的三张卡片中随机抽取一张卡片记下数字．设小红抽到的数字为x，小明抽到的数字为y，点A的坐标为（x，y）．

(1)、请用列表法或画树状图的方法列出点A所有结果；

(2)、若点A在坐标轴上，则小红胜；反之，则小明胜．请你用概率的相关知识解释这个游戏是否公平？

查看试题解析
21. 如图，在四边形ABCD的中，AB∥CD，对角线AC，BD相交于点O，且AO＝CO，△OAB是等边三角形．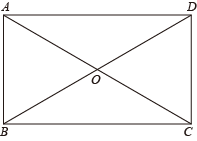

(1)、求证：四边形ABCD是矩形；

(2)、若S_四_边_形ABCD＝4 $\sqrt{3}$ ，求BD的长．

查看试题解析
22. 在乡村振兴活动中，某电商正在热销一种当地特色商品，其成本为50元/件，在销售过程中发现随着售价增加，销售量在减少．商家决定当售价为80元/件时，改变销售策略，此时售价每增加1元需支付由此产生的额外费用400元．该商品销售量y（件）与售价x（元/件）满足如图所示的函数关系（其中50≤x≤90，且x为整数）．

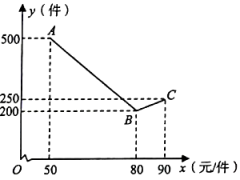(1)、直接写出y与x的函数关系式；

(2)、当售价为多少时，商家所获利润最大，最大利润是多少？

查看试题解析
23. 如图， $A B$ 是 $⊙ O$ 的直径，点C是 $⊙ O$ 上一点（与点A，B不重合），过点C作直线 $M N$ ，使得 $∠ A C N = ∠ A B C$ ．

(1)、求证：直线 $M N$ 是 $⊙ O$ 的切线．

(2)、过点A作 $A D ⊥ M N$ 于点D，交 $⊙ O$ 于点E，若 $⊙ O$ 的半径为6， $s i n ∠ D A C = \frac{1}{2}$ ，求图中阴影部分（弓形）的面积．

查看试题解析
24. 已知抛物线y＝mx²﹣3mx﹣18m（m是常数，且m≠0）．

(1)、证明：抛物线与x轴总有两个交点；并求出这两个交点A、B（A在B的左侧）的坐标；

(2)、若点C（1，5）和D（5，n）在抛物线上，点P是线段AB上的点．且有 $\frac{P A}{P B} = \frac{3}{5}$ ．请判断△PCD的形状；

(3)、在抛物线上是否存在点Q，使得S△QCD＝S△OCD？若存在，求出满足条件的点Q的坐标；若不存在，请说明理由．

查看试题解析

年级	平均数	众数	中位数	6分以上人数百分比
七年级	7.5	7	b	c
八年级	7.5	a	7.5	90%