山东省青岛市即墨区2022年中考一模数学试题
试卷更新日期:2022-04-29 类型:中考模拟
一、单选题
-
1. -2的倒数是( )A、-2 B、2 C、 D、2. 下列图形中,是轴对称图形且对称轴条数最多的是( )A、
 B、
B、 C、
C、 D、
D、 3. 2022年2月,北京冬奥会的成功举办,我国已实现了“带动三亿人参与冰雪运动”的目标.数据显示,全国居民参与过冰雪运动的人数为3.46亿人,冰雪运动参与率24.56%.数据“3.46亿”用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,△ABC的顶点坐标分别为A(4,6)、B(5,2)、C(2,1),如果将△ABC绕点B按顺时针方向旋转90°,得到△A′BC′,将△A′BC′向下平移2个单位,得△A″B′C″,那么点C的对应点C″的坐标是( )
3. 2022年2月,北京冬奥会的成功举办,我国已实现了“带动三亿人参与冰雪运动”的目标.数据显示,全国居民参与过冰雪运动的人数为3.46亿人,冰雪运动参与率24.56%.数据“3.46亿”用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,△ABC的顶点坐标分别为A(4,6)、B(5,2)、C(2,1),如果将△ABC绕点B按顺时针方向旋转90°,得到△A′BC′,将△A′BC′向下平移2个单位,得△A″B′C″,那么点C的对应点C″的坐标是( ) A、 B、 C、 D、6. 如图,在中, , 以点A为圆心,3为半径的圆与边相切于点D,与 , 分别交于点E和点G,点F是优弧上一点, , 则的度数是( )
A、 B、 C、 D、6. 如图,在中, , 以点A为圆心,3为半径的圆与边相切于点D,与 , 分别交于点E和点G,点F是优弧上一点, , 则的度数是( )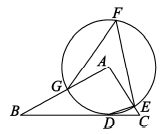 A、50° B、48° C、45° D、36°7. 如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( ).
A、50° B、48° C、45° D、36°7. 如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( ). A、 B、 C、 D、8. 一次函数 与二次函数 在同一平面直角坐标系中的图象可能是( )A、
A、 B、 C、 D、8. 一次函数 与二次函数 在同一平面直角坐标系中的图象可能是( )A、 B、
B、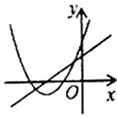 C、
C、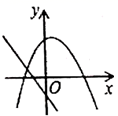 D、
D、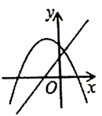
二、填空题
-
9. 计算: .10. 三棱柱的三视图如图所示,在俯视图△EFG中,FG=18cm,EG=14cm,∠EGF=30°,则左视图中AB的长为cm.
 11. 一个口袋中有红球、白球共20个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了100次球,发现有70次摸到红球.请你估计这个口袋中有个白球.12. 如图,点 是 上的点,连接 ,且 ,过点O作 交 于点D,连接 ,已知 半径为2,则图中阴影面积为.
11. 一个口袋中有红球、白球共20个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了100次球,发现有70次摸到红球.请你估计这个口袋中有个白球.12. 如图,点 是 上的点,连接 ,且 ,过点O作 交 于点D,连接 ,已知 半径为2,则图中阴影面积为. 13. 如图,在平面直角坐标系中,四边形的边与x轴的正半轴重合, , 轴,对角线交于点M.已知 , 的面积为4.若反比例函数的图象恰好经过点M,则k的值为 .
13. 如图,在平面直角坐标系中,四边形的边与x轴的正半轴重合, , 轴,对角线交于点M.已知 , 的面积为4.若反比例函数的图象恰好经过点M,则k的值为 .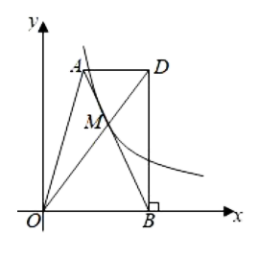 14. 如图,已知正方形ABCD,点E是BC边上一点,将△ABE沿直线AE折叠,点B落在F处,连接BF并延长,与∠DAF的平分线相交于点H,与AE,CD分别相交于点G,M,连接HC,DH,DF,若AB=3,BE=1,则DH= .
14. 如图,已知正方形ABCD,点E是BC边上一点,将△ABE沿直线AE折叠,点B落在F处,连接BF并延长,与∠DAF的平分线相交于点H,与AE,CD分别相交于点G,M,连接HC,DH,DF,若AB=3,BE=1,则DH= .
三、解答题
-
15. 如图,已知线段MN=a,AR⊥AK,垂足为A.求作四边形ABCD,使得点B,D分别在射线AK,AR上,∠ABC=60°且AB=BC=a,CD∥AB(要求:尺规作图,不写作法,保留作图痕迹).
 16.(1)、化简:(2)、解不等式组:17. 某校计划组织学生参加“书法”、“摄影”、“航模”、“围棋”四个课外兴题小组.要求每人必须参加.并且只能选择其中一个小组,为了解学生对四个课外兴趣小组的选择情况,学校从全体学生中随机抽取部分学生进行问卷调查,并把调查结果制成如图所示的扇形统计图和条形统计图(部分信息未给出).请你根据给出的信息解答下列问题:
16.(1)、化简:(2)、解不等式组:17. 某校计划组织学生参加“书法”、“摄影”、“航模”、“围棋”四个课外兴题小组.要求每人必须参加.并且只能选择其中一个小组,为了解学生对四个课外兴趣小组的选择情况,学校从全体学生中随机抽取部分学生进行问卷调查,并把调查结果制成如图所示的扇形统计图和条形统计图(部分信息未给出).请你根据给出的信息解答下列问题:
 (1)、求参加这次问卷调查的学生人数.并补全条形统计图(画图后请标注相应的数据);(2)、m= , n=;(3)、若某校共有1200名学生,试估计该校选择“围棋”课外兴趣小组有多少人?18. 某品牌免洗洗手液按剂型分为凝胶型、液体型,泡沫型三种型号(分别用A,B,C依次表示这三种型号).小辰和小安计划每人购买一瓶该品牌免洗洗手液,上述三种型号中的每一种免洗洗手液被选中的可能性均相同.(1)、小辰随机选择一种型号是凝胶型免洗洗手液的概率是 .(2)、请你用列表法或画树状图法,求小辰和小安选择同一种型号免洗洗手液的概率.19. 王刚同学在学习了解直角三角形及其应用的知识后,尝试利用所学知识测量河对岸大树AB的高度,如图,他在点C处测得大树顶端A的仰角为45°,再从C点出发沿斜坡走2米到达斜坡上D点,在点D处测得树顶端A的仰角为30°,若斜坡CF的坡比为i=1:3(点E,C,B在同一水平线上).求大树AB的高度(≈1.73,结果保留整数).
(1)、求参加这次问卷调查的学生人数.并补全条形统计图(画图后请标注相应的数据);(2)、m= , n=;(3)、若某校共有1200名学生,试估计该校选择“围棋”课外兴趣小组有多少人?18. 某品牌免洗洗手液按剂型分为凝胶型、液体型,泡沫型三种型号(分别用A,B,C依次表示这三种型号).小辰和小安计划每人购买一瓶该品牌免洗洗手液,上述三种型号中的每一种免洗洗手液被选中的可能性均相同.(1)、小辰随机选择一种型号是凝胶型免洗洗手液的概率是 .(2)、请你用列表法或画树状图法,求小辰和小安选择同一种型号免洗洗手液的概率.19. 王刚同学在学习了解直角三角形及其应用的知识后,尝试利用所学知识测量河对岸大树AB的高度,如图,他在点C处测得大树顶端A的仰角为45°,再从C点出发沿斜坡走2米到达斜坡上D点,在点D处测得树顶端A的仰角为30°,若斜坡CF的坡比为i=1:3(点E,C,B在同一水平线上).求大树AB的高度(≈1.73,结果保留整数). 20. 某电商积极响应市政府号召,在线销售甲、乙、丙三种农产品.已知 乙产品的售价比 甲产品的售价多5元, 丙产品的售价是 甲产品售价的3倍,用270元购买丙产品的数量是用60元购买乙产品数量的3倍.(1)、求甲、乙、丙三种农产品每千克的售价分别是多少元?(2)、电商推出如下销售方案:甲、乙、丙三种农产品搭配销售共 ,其中乙产品的数量是丙产品数量的2倍,且甲、丙两种产品数量之和不超过乙产品数量的3倍.请你帮忙计算,按此方案购买 农产品最少要花费多少元?21. 已知:如图,在四边形ABCD中,∠ABC=90°,AD∥BC,DE⊥AC于点F,交BC于点G,交AB的延长线于点E,且AE=AC.
20. 某电商积极响应市政府号召,在线销售甲、乙、丙三种农产品.已知 乙产品的售价比 甲产品的售价多5元, 丙产品的售价是 甲产品售价的3倍,用270元购买丙产品的数量是用60元购买乙产品数量的3倍.(1)、求甲、乙、丙三种农产品每千克的售价分别是多少元?(2)、电商推出如下销售方案:甲、乙、丙三种农产品搭配销售共 ,其中乙产品的数量是丙产品数量的2倍,且甲、丙两种产品数量之和不超过乙产品数量的3倍.请你帮忙计算,按此方案购买 农产品最少要花费多少元?21. 已知:如图,在四边形ABCD中,∠ABC=90°,AD∥BC,DE⊥AC于点F,交BC于点G,交AB的延长线于点E,且AE=AC. (1)、求证:AB=AF;(2)、若∠ACB=30°,连接AG,判断四边形AGCD是什么特殊的四边形?并证明你的结论.22. 北京2022年冬奥会跳台滑雪比赛在张家口赛区进行,如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系,图中的抛物线近似表示滑雪场地上的一座小山坡,某运动员从点O正上方4米处的A点滑出,滑出后沿段抛物线运动.
(1)、求证:AB=AF;(2)、若∠ACB=30°,连接AG,判断四边形AGCD是什么特殊的四边形?并证明你的结论.22. 北京2022年冬奥会跳台滑雪比赛在张家口赛区进行,如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系,图中的抛物线近似表示滑雪场地上的一座小山坡,某运动员从点O正上方4米处的A点滑出,滑出后沿段抛物线运动. (1)、当运动员运动到离A处的水平距离为4米时,离水平线的高度为8米,求抛物线的函数关系式(不要求写出自变量x的取值范围);(2)、在(1)的条件下,求运动员在落在小山坡上之前滑行的水平距离,并求出在滑行期间距离小山坡的最大高度是多少米?(3)、当运动员运动到坡顶正上方,且与坡顶距离超过2.3米时,求b的取值范围.23. 课本再现
(1)、当运动员运动到离A处的水平距离为4米时,离水平线的高度为8米,求抛物线的函数关系式(不要求写出自变量x的取值范围);(2)、在(1)的条件下,求运动员在落在小山坡上之前滑行的水平距离,并求出在滑行期间距离小山坡的最大高度是多少米?(3)、当运动员运动到坡顶正上方,且与坡顶距离超过2.3米时,求b的取值范围.23. 课本再现 (1)、在证明“三角形内角和定理”时,小明只撕下三角形纸片的一个角拼成图1即可证明,其中与相等的角是;(2)、类比迁移
(1)、在证明“三角形内角和定理”时,小明只撕下三角形纸片的一个角拼成图1即可证明,其中与相等的角是;(2)、类比迁移如图2,在四边形中,与互余,小明发现四边形中这对互余的角可类比(1)中思路进行拼合:先作 , 再过点作于点 , 连接 , 发现 , , 之间的数量关系是;
(3)、方法运用
如图3,在四边形中,连接 , , 点是两边垂直平分线的交点,连接 , .
①求证:;
②连接 , 如图4,已知 , , , 求的长(用含 , 的式子表示).
24. 如图,在△ABC中,∠ACB=90°,AC=8,BC=6,点D是BC中点,连接CD,动点P从点C出发沿折线CD-DB方向以每秒2个单位长度的速度向终点B运动.过点P作PE⊥AC,垂足为点E,以PE、PD为邻边作平行四边形PDFE. 设点P的运动时间为t(秒). (1)、CD= .(2)、当点P在BD上时,求FD的长度(用含t的代数式表示).(3)、当平行四边形PDFE与△ACD重合部分图形的面积为S时,求S与t之间的函数关系式.(4)、当点F落在△ABC的某个内角平分线上时请直接写出t的值.
(1)、CD= .(2)、当点P在BD上时,求FD的长度(用含t的代数式表示).(3)、当平行四边形PDFE与△ACD重合部分图形的面积为S时,求S与t之间的函数关系式.(4)、当点F落在△ABC的某个内角平分线上时请直接写出t的值.