山东省聊城市莘县2022年中考一模数学试题
试卷更新日期:2022-04-29 类型:中考模拟
一、单选题
-
1. ﹣ 的倒数是( )A、3 B、﹣3 C、 D、﹣2. 下列设计的图案中,是中心对称图形但不是轴对称图形的是( )A、
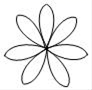 B、
B、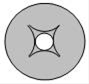 C、
C、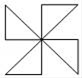 D、
D、 3. 在运算速度上,已连续多次取得世界第一的神威太湖之光超级计算机,其峰值性能为12.5亿亿次/秒.这个数据以亿次/秒为单位用科学记数法可以表示为( )A、亿次/秒 B、亿次/秒 C、亿次/秒 D、亿次/秒4. 把一副三角板放在同一水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,则∠1的度数是( )
3. 在运算速度上,已连续多次取得世界第一的神威太湖之光超级计算机,其峰值性能为12.5亿亿次/秒.这个数据以亿次/秒为单位用科学记数法可以表示为( )A、亿次/秒 B、亿次/秒 C、亿次/秒 D、亿次/秒4. 把一副三角板放在同一水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,则∠1的度数是( )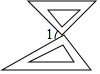 A、45° B、60° C、75° D、82.5°5. 下列说法正确的是( )A、367人中至少有2人生日相同 B、任意掷一枚均匀的骰子,掷出的点数是偶数的概率是 C、天气预报说明天的降水概率为90%,则明天一定会下雨 D、某种彩票中奖的概率是1%,则买100张彩票一定有1张中6. 下列各式不成立的是( )A、 B、 C、 D、7. 为了增强学生预防新冠肺炎的安全意识,某校开展疫情防控知识竞赛.来自不同年级的30名参赛同学的得分情况如下表所示,这些成绩的中位数和众数分别是( )
A、45° B、60° C、75° D、82.5°5. 下列说法正确的是( )A、367人中至少有2人生日相同 B、任意掷一枚均匀的骰子,掷出的点数是偶数的概率是 C、天气预报说明天的降水概率为90%,则明天一定会下雨 D、某种彩票中奖的概率是1%,则买100张彩票一定有1张中6. 下列各式不成立的是( )A、 B、 C、 D、7. 为了增强学生预防新冠肺炎的安全意识,某校开展疫情防控知识竞赛.来自不同年级的30名参赛同学的得分情况如下表所示,这些成绩的中位数和众数分别是( )成绩/分
84
88
92
96
100
人数/人
2
4
9
10
5
A、92分,96分 B、94分,96分 C、96分,96分 D、96分,100分8. 如图, 是半圆 的直径, , 是 上两点,连接 , 并延长交于点 ,连接 , ,如果 ,那么 的度数为( )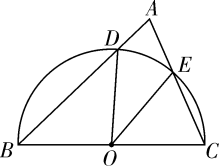 A、 B、 C、 D、9. 在平面直角坐标系中,点 是线段 上一点,以原点 为位似中心把 放大到原来的两倍,则点 的对应点的坐标为( )A、 B、 或 C、 D、 或10. 已知关于x的一元二次方程有两个不相等的实数根x1 , x2 . 若 , 则m的值是( )A、2 B、﹣1 C、2或﹣1 D、不存在11. 如图,在矩形ABCD中,点E在DC上,将矩形沿AE折叠,使点D落在BC边上的点F处.若AB=3,BC=5,则tan∠DAE的值为( )
A、 B、 C、 D、9. 在平面直角坐标系中,点 是线段 上一点,以原点 为位似中心把 放大到原来的两倍,则点 的对应点的坐标为( )A、 B、 或 C、 D、 或10. 已知关于x的一元二次方程有两个不相等的实数根x1 , x2 . 若 , 则m的值是( )A、2 B、﹣1 C、2或﹣1 D、不存在11. 如图,在矩形ABCD中,点E在DC上,将矩形沿AE折叠,使点D落在BC边上的点F处.若AB=3,BC=5,则tan∠DAE的值为( )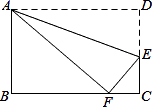 A、 B、 C、 D、12. 如图,菱形ABCD的边长是4厘米,∠B=60°,动点P以1厘米/秒的速度自A点出发沿AB方向运动至B点停止,动点Q以2厘米/秒的速度自B点出发沿折线BCD运动至D点停止.若点P、Q同时出发运动了t秒,记△BPQ的面积为S厘米2 , 下面图象中能表示S与t之间的函数关系的是( )
A、 B、 C、 D、12. 如图,菱形ABCD的边长是4厘米,∠B=60°,动点P以1厘米/秒的速度自A点出发沿AB方向运动至B点停止,动点Q以2厘米/秒的速度自B点出发沿折线BCD运动至D点停止.若点P、Q同时出发运动了t秒,记△BPQ的面积为S厘米2 , 下面图象中能表示S与t之间的函数关系的是( )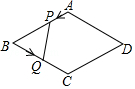 A、
A、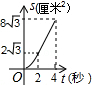 B、
B、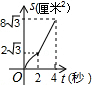 C、
C、 D、
D、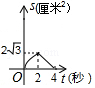
二、填空题
-
13. 计算:(﹣﹣)÷= .14. 用一块圆心角为 的扇形铁皮,做一个高为 的圆锥形工件(接缝忽略不计),那么这个扇形铁皮的半径是 .15. 莘县政府街十字路口设有交通信号灯,东西向信号灯的开启规律如下:绿灯开启42秒后关闭,紧接着黄灯开启3秒后关闭,再紧接着红灯开启30秒.按此规律循环下去.如果不考虑其他因素,当一辆汽车沿东西方向随机地行驶到该路口时,遇到红灯的概率是 .
 16. 如图①是山东舰航徽的构图,采用航母45度破浪而出的角度,展现山东舰作为中国首艘国产舰母横空出世的气势,将舰徽中第一条波浪抽象成几何图形,则是一条长为 的弧,若该弧所在的扇形是高为12的圆锥侧面展开图(如图②),则该圆锥的母线长 为.
16. 如图①是山东舰航徽的构图,采用航母45度破浪而出的角度,展现山东舰作为中国首艘国产舰母横空出世的气势,将舰徽中第一条波浪抽象成几何图形,则是一条长为 的弧,若该弧所在的扇形是高为12的圆锥侧面展开图(如图②),则该圆锥的母线长 为.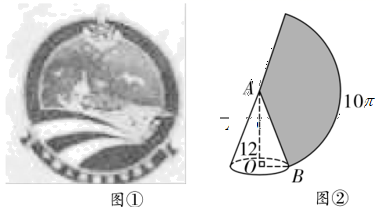 17. 如图,一块试验田的形状是三角形(设其为△ABC),管理员从BC边上的一点D出发,沿DC→CA→AB→BD的方向走了一圈回到D处,则管理员从出发到回到原处在途中身体转过°.
17. 如图,一块试验田的形状是三角形(设其为△ABC),管理员从BC边上的一点D出发,沿DC→CA→AB→BD的方向走了一圈回到D处,则管理员从出发到回到原处在途中身体转过°.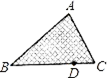
三、解答题
-
18. 解不等式组 , 并写出它的正整数解.19. 先化简,再求值:(1+ )÷ ,其中x满足x2﹣2x﹣5=0.20. 如图,正方形 中, 是 上的一点,连接 ,过 点作 ,垂足为点 ,延长 交 于点 ,连接 .
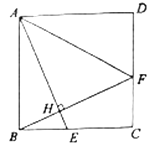 (1)、求证: .
(1)、求证: .
(2)、若正方形边长是5, ,求 的长.21. 如图,一次函数y=-x+1的图象与两坐标轴分别交于A,B两点,与反比例函数的图象交于点 .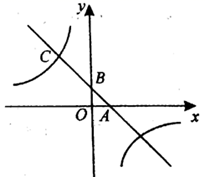 (1)、求反比例函数的解析式;(2)、若点P在y轴正半轴上,且与点B,C构成以 为腰的等腰三角形,请求出所有符合条件的P点坐标.22. 八年级(1)班研究性学习小组为研究全校同学课外阅读情况,在全校随机邀请了部分同学参与问卷调查,统计同学们一个月阅读课外书的数量,并绘制了以下统计图.
(1)、求反比例函数的解析式;(2)、若点P在y轴正半轴上,且与点B,C构成以 为腰的等腰三角形,请求出所有符合条件的P点坐标.22. 八年级(1)班研究性学习小组为研究全校同学课外阅读情况,在全校随机邀请了部分同学参与问卷调查,统计同学们一个月阅读课外书的数量,并绘制了以下统计图.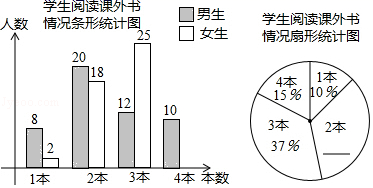
请根据图中信息解决下列问题:
(1)、共有多少名同学参与问卷调查;(2)、补全条形统计图和扇形统计图;(3)、全校共有学生1500人,请估计该校学生一个月阅读2本课外书的人数约为多少.23. 甲、乙两人加工同一种零件,甲每天加工的数量是乙每天加工数量的 1.5 倍,两人各加工 600 个这种零件,甲比乙少用 5 天.(1)、求甲、乙两人每天各加工多少个这种零件?(2)、已知甲、乙两人加工这种零件每天的加工费分别是 150 元和 120 元,现有 3000 个这种零件的加工任务,甲单独加工一段时间后另有安排,剩余任务由乙单独完成.如果总加工费不超过 7800 元,那么甲至少加工了多少天?24. 如图,在 中, , ,点C是 的中点,以 为半径作⊙O.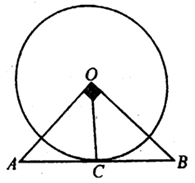 (1)、求证: 是⊙O的切线;(2)、若 ,求 的长.25. 如图1,在平面直角坐标系中,抛物线y=ax2﹣4ax﹣6(a>0)与x轴交于A,B两点,且OB=3OA,与y轴交于点C,抛物线的顶点为D,对称轴与x轴交于点E.
(1)、求证: 是⊙O的切线;(2)、若 ,求 的长.25. 如图1,在平面直角坐标系中,抛物线y=ax2﹣4ax﹣6(a>0)与x轴交于A,B两点,且OB=3OA,与y轴交于点C,抛物线的顶点为D,对称轴与x轴交于点E.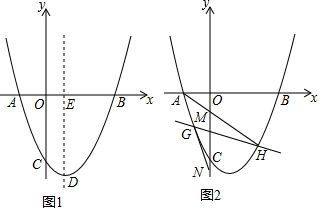 (1)、求该抛物线的解析式,并直接写出顶点D的坐标;(2)、如图2,直线y= +n与抛物线交于G,H两点,直线AH,AG分别交y轴负半轴于M,N两点,求OM+ON的值;(3)、如图1,点P在线段DE上,作等腰△BPQ,使得PB=PQ,且点Q落在直线CD上,若满足条件的点Q有且只有一个,求点P的坐标.
(1)、求该抛物线的解析式,并直接写出顶点D的坐标;(2)、如图2,直线y= +n与抛物线交于G,H两点,直线AH,AG分别交y轴负半轴于M,N两点,求OM+ON的值;(3)、如图1,点P在线段DE上,作等腰△BPQ,使得PB=PQ,且点Q落在直线CD上,若满足条件的点Q有且只有一个,求点P的坐标.