山东省济宁市汶上县2022年中考一模数学试题
试卷更新日期:2022-04-29 类型:中考模拟
一、单选题
-
1. 下列各数中为无理数的是( )A、0 B、-0.5 C、 D、-22. 如图,直线 , , 则等于( )
 A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 在四张反面无差别的卡片上,其正面分别印有线段、等边三角形、平行四边形和正六边形.现将四张卡片的正面朝下放置,混合均匀后从中随机抽取两张,则抽到的卡片正面图形都是轴对称图形的概率为( )A、 B、 C、 D、5. 如图,将△ABC绕点A逆时针旋转一定角度得到△ADE.若∠BAC =85°,∠E=70°,且AD⊥BC,则旋转角的度数为( )
A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 在四张反面无差别的卡片上,其正面分别印有线段、等边三角形、平行四边形和正六边形.现将四张卡片的正面朝下放置,混合均匀后从中随机抽取两张,则抽到的卡片正面图形都是轴对称图形的概率为( )A、 B、 C、 D、5. 如图,将△ABC绕点A逆时针旋转一定角度得到△ADE.若∠BAC =85°,∠E=70°,且AD⊥BC,则旋转角的度数为( ) A、65° B、70° C、75° D、85°6. 如图所示,在△ABC中,DFAC,DEBC,AE=4,EC=2,BC=8,则CF为( )
A、65° B、70° C、75° D、85°6. 如图所示,在△ABC中,DFAC,DEBC,AE=4,EC=2,BC=8,则CF为( ) A、 B、 C、 D、67. 关于的一元二次方程有两个相等的实数根,点、是反比例函数的图象上的两个点,若 , 则、的大小关系为( )A、 B、 C、 D、不能确定8. 如图,为⊙O的直径,弦于点E,直线l切⊙O于点C,延长交l于点F,若 , , 则的长度为( )
A、 B、 C、 D、67. 关于的一元二次方程有两个相等的实数根,点、是反比例函数的图象上的两个点,若 , 则、的大小关系为( )A、 B、 C、 D、不能确定8. 如图,为⊙O的直径,弦于点E,直线l切⊙O于点C,延长交l于点F,若 , , 则的长度为( )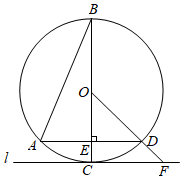 A、2 B、 C、 D、49. 如图,抛物线 与 轴只有一个公共点A(1,0),与 轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线 ,则图中两个阴影部分的面积和为( )
A、2 B、 C、 D、49. 如图,抛物线 与 轴只有一个公共点A(1,0),与 轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线 ,则图中两个阴影部分的面积和为( ) A、1 B、2 C、3 D、410. 规定: 给出以下四个结论:(1) ;(2) ;(3) ;(4) 其中正确的结论的个数为( )A、1个 B、2个 C、3个 D、4个
A、1 B、2 C、3 D、410. 规定: 给出以下四个结论:(1) ;(2) ;(3) ;(4) 其中正确的结论的个数为( )A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 第七次全国人口普查数据显示,山东省常住人口约为10152.7万人,将10152.7万用科学记数法(精确到十万位)可表示为 .12. 分解因式: .13. 如图,在 中,点D是边BC上的一点.若 , ,则∠C的大小为 .
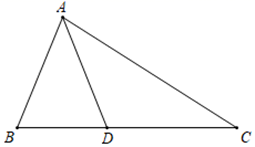 14. 如图,内接于于点H,若 , 的半径为7,则AB= .
14. 如图,内接于于点H,若 , 的半径为7,则AB= . 15. 如图,直线 与反比例函数 的图象交于A,B两点,与x轴交于点C,且 ,连接OA.已知 的面积为12,则k的值为.
15. 如图,直线 与反比例函数 的图象交于A,B两点,与x轴交于点C,且 ,连接OA.已知 的面积为12,则k的值为.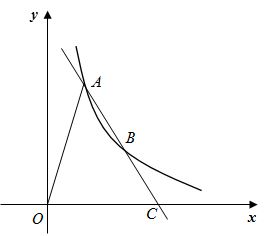
三、解答题
-
16. 先化简,再求值: , 其中 .17. 某中学为了解初三学生参加志愿者活动的次数,随机调查了该年级20名学生,统计得到该20名学生参加志愿者活动的次数如下:3;5;3;6;3;4;4;5;2;4;5;6;1;3;5;5;4;4;2;4
根据以上数据,得到如下不完整的频数分布表:
次数
1
2
3
4
5
6
人数
1
2
a
6
b
2
(1)、表格中的 , ;(2)、在这次调查中,参加志愿者活动的次数的众数为 , 中位数为;(3)、若该校初三年级共有300名学生,根据调查统计结果,估计该校初三年级学生参加志愿者活动的次数为4次的人数.18. 避雷针是用来保护建筑物、高大树木等避免雷击的装置.如图,小陶同学要测量垂直于地面的大楼 顶部避雷针 的长度( , , 三点共线),在水平地面 点测得 , , 点与大楼底部 点的距离 ,求避雷针 的长度.(结果精确到 .参考数据: , , , , , ) 19. 某商品原来每件的售价为60元,经过两次降价后每件的售价为48.6元,并且每次降价的百分率相同.(1)、求该商品每次降价的百分率;(2)、若该商品每件的进价为40元,计划通过以上两次降价的方式,将库存的该商品20件全部售出,并且确保两次降价销售的总利润不少于200元,那么第一次降价至少售出多少件后,方可进行第二次降价?20. 如图,是以为直径的的切线,切点为点 , 过点作 , 垂足为点 , 交于点 .
19. 某商品原来每件的售价为60元,经过两次降价后每件的售价为48.6元,并且每次降价的百分率相同.(1)、求该商品每次降价的百分率;(2)、若该商品每件的进价为40元,计划通过以上两次降价的方式,将库存的该商品20件全部售出,并且确保两次降价销售的总利润不少于200元,那么第一次降价至少售出多少件后,方可进行第二次降价?20. 如图,是以为直径的的切线,切点为点 , 过点作 , 垂足为点 , 交于点 . (1)、求证:PB是的切线;(2)、若 , , 求的长.21. 已知正方形 , E,为平面内两点.
(1)、求证:PB是的切线;(2)、若 , , 求的长.21. 已知正方形 , E,为平面内两点. (1)、【探究建模】如图1,当点E在边上时, , 且B,C,三点共线,求证:;(2)、【类比应用】如图2,当点E在正方形外部时, , , 且E,C,F三点共线,猜想并证明线段AE,CF之间的数量关系;(3)、【拓展迁移】如图3,当点E在正方形外部时, , , , 且D,F,E三点共线,DE与AB交于点 . 若 , , 请直接写出DE的长.22. 如图1,二次函数的图象交轴于点 , 交轴于点 , 点为轴上一动点.
(1)、【探究建模】如图1,当点E在边上时, , 且B,C,三点共线,求证:;(2)、【类比应用】如图2,当点E在正方形外部时, , , 且E,C,F三点共线,猜想并证明线段AE,CF之间的数量关系;(3)、【拓展迁移】如图3,当点E在正方形外部时, , , , 且D,F,E三点共线,DE与AB交于点 . 若 , , 请直接写出DE的长.22. 如图1,二次函数的图象交轴于点 , 交轴于点 , 点为轴上一动点. (1)、求二次函数的表达式并化成一般形式;(2)、过点作轴交线段于点 , 交抛物线于点 , 连接 . 当时,求的面积;(3)、如图2,将线段绕点逆时针旋转得到线段 . 当点D在轴下方的抛物线上时,求点D的坐标.
(1)、求二次函数的表达式并化成一般形式;(2)、过点作轴交线段于点 , 交抛物线于点 , 连接 . 当时,求的面积;(3)、如图2,将线段绕点逆时针旋转得到线段 . 当点D在轴下方的抛物线上时,求点D的坐标.