山东省济宁市泗水县2022年中考一模数学试题
试卷更新日期:2022-04-29 类型:中考模拟
一、单选题
-
1. 在 , , 0,2四个数中,最大的数是( )A、2 B、0 C、 D、2. 2022年新年贺词中提到“人不负青山,青山定不负人”,下列四个有关环保的图形中,是轴对称图形,但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 近年来,新冠肺炎给人类带来了巨大灾难,经科学家研究,冠状病毒多数为球形或近似球形,其直径约为0.00000011米,其中数据0.00000011用科学记数法表示正确的是( )A、 B、 C、 D、4. 下列计算正确的是( )A、 =±4 B、﹣ =﹣8 C、 =2 D、﹣5. 现有一组数据分别是5、4、6、5、4、13、5,关于这组数据下列说法正确的是( )A、中位数是4 B、众数是7 C、中位数和众数都是5 D、中位数和平均数都是56. 《九章算术》是中国古代的一本重要数学著作,其中有一道方程的应用题:“五只雀、六只燕,共重16两,雀重燕轻.互换其中一只,恰好一样重.问每只雀、燕的重量各为多少?”解:设雀每只x两,燕每只y两,则可列出方程组为( )A、 B、 C、 D、7. 如图是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积是( )
3. 近年来,新冠肺炎给人类带来了巨大灾难,经科学家研究,冠状病毒多数为球形或近似球形,其直径约为0.00000011米,其中数据0.00000011用科学记数法表示正确的是( )A、 B、 C、 D、4. 下列计算正确的是( )A、 =±4 B、﹣ =﹣8 C、 =2 D、﹣5. 现有一组数据分别是5、4、6、5、4、13、5,关于这组数据下列说法正确的是( )A、中位数是4 B、众数是7 C、中位数和众数都是5 D、中位数和平均数都是56. 《九章算术》是中国古代的一本重要数学著作,其中有一道方程的应用题:“五只雀、六只燕,共重16两,雀重燕轻.互换其中一只,恰好一样重.问每只雀、燕的重量各为多少?”解:设雀每只x两,燕每只y两,则可列出方程组为( )A、 B、 C、 D、7. 如图是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积是( )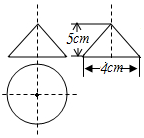 A、 B、 C、 D、8. 如图,一圆环分别与夹角为的两墙面相切,圆环上图示位置固定一小球,并用细线将小球与两切点分别相连,两细线夹角为 , 则与之间的关系是( )
A、 B、 C、 D、8. 如图,一圆环分别与夹角为的两墙面相切,圆环上图示位置固定一小球,并用细线将小球与两切点分别相连,两细线夹角为 , 则与之间的关系是( ) A、 B、 C、 D、9. 如图中,分别是由1个、2个、个(为正整数)正方形连接成的图形,在图1中,;在图2中,;通过以上计算,请写出图3中____(用含的式子表示)
A、 B、 C、 D、9. 如图中,分别是由1个、2个、个(为正整数)正方形连接成的图形,在图1中,;在图2中,;通过以上计算,请写出图3中____(用含的式子表示) A、 B、 C、 D、
A、 B、 C、 D、二、解答题
-
10. 某中学九年级数学兴趣小组的同学准备测量校内旗杆的高度,他们在点测得旗杆顶端的仰角 , 向前走了30米到达点,在点测得旗杆顶端A的仰角 , 则旗杆的高为多少米?( )
 A、15米 B、米 C、米 D、米11. 先化简,再求值 , 其 , .12. 为了解同学们对新冠疫情相关知识的掌握情况,增强同学们的防控意识,某校对八年级甲、乙两班各50名学生进行了新冠疫情相关知识的测试,并分别抽取了10份成绩,整理分析过程如下,请补充完整.
A、15米 B、米 C、米 D、米11. 先化简,再求值 , 其 , .12. 为了解同学们对新冠疫情相关知识的掌握情况,增强同学们的防控意识,某校对八年级甲、乙两班各50名学生进行了新冠疫情相关知识的测试,并分别抽取了10份成绩,整理分析过程如下,请补充完整.
【收集数据】(满分100分)
甲班10名学生的测试成绩统计如下:89,85,82,85,92,80,85,77,85,80
乙班10名学生的测试成绩统计如下:86,89,83,80,80,80,84,82,93,83
【整理数据】按如下分数段整理、描述这两组样本数据组别
组别
75.5~80.5
80.5~85.5
85.5~90.5
90.5~95.5
甲
1
1
乙
3
4
2
1
请回答下列问题
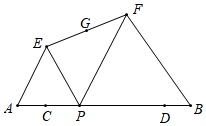
(1)、在表中,a= , b= .(2)、补全乙班10名学生测试成绩的频数分布直方图(3)、若规定得分在85分及以上(含85分)为合格,请估计甲班50名学生中疫情防控相关知识合格的学生有人.(4)、为继续宣传新冠疫苗接种的重要性,某小区物业部门准备在已经接种疫苗的居民中招募2名志愿宣传者,现有2名男性2名女性共4名居民报名.请用列表或画树状图的方法,求要从这4人中随机挑选2人,恰好抽到一名男性和一名女性的概率13. 如图,在中, (1)、求作的平分线,交于点 , 再作的垂直平分线,分别交于点 , 交于点 . 连接 , (保留作图痕迹,不写作法)(2)、若 , , . 则的长是多少?14. 某学校购进一批成捆的 , 两种图书,每捆种图书比每捆种图书多10本,每捆种图书和每捆种图书的价格分别是630元和600元,而每本种图书和每本种图书的价格分别是这一批图书平均每本价格的0.9倍和1.2倍.(1)、求这一批图书平均每本的价格是多少元?(2)、如果购进的这批图书共550本,种图书至多购进350本,为了使购进的这批图书的费用最低,应购进种图书和种图书各多少本?并求出最低费用.15. 有一张矩形纸片 , , 分别是边 , 上的点(不与顶点重合),如图所示,若将矩形分成面积相等的两部分.求证: .
(1)、求作的平分线,交于点 , 再作的垂直平分线,分别交于点 , 交于点 . 连接 , (保留作图痕迹,不写作法)(2)、若 , , . 则的长是多少?14. 某学校购进一批成捆的 , 两种图书,每捆种图书比每捆种图书多10本,每捆种图书和每捆种图书的价格分别是630元和600元,而每本种图书和每本种图书的价格分别是这一批图书平均每本价格的0.9倍和1.2倍.(1)、求这一批图书平均每本的价格是多少元?(2)、如果购进的这批图书共550本,种图书至多购进350本,为了使购进的这批图书的费用最低,应购进种图书和种图书各多少本?并求出最低费用.15. 有一张矩形纸片 , , 分别是边 , 上的点(不与顶点重合),如图所示,若将矩形分成面积相等的两部分.求证: . 16. 阅读资料:如图1,在平面之间坐标系中, , 两点的坐标分别为 , , 由勾股定理得 , 所以 , 两点间的距离为 . 我们知道,圆可以看成到圆心距离等于半径的点的集合,如图2,在平面直角坐标系中,为圆上任意一点,则到原点的距离的平方为 , 当的半径为时,的方程可写为: .
16. 阅读资料:如图1,在平面之间坐标系中, , 两点的坐标分别为 , , 由勾股定理得 , 所以 , 两点间的距离为 . 我们知道,圆可以看成到圆心距离等于半径的点的集合,如图2,在平面直角坐标系中,为圆上任意一点,则到原点的距离的平方为 , 当的半径为时,的方程可写为: .问题拓展:如果圆心坐标为 , 半径为 , 那么的方程可以写为 .
综合应用:如图3,与轴相切于原点 , 点坐标为 , 是上一点,连接 , 使 , 作 , 垂足为 , 延长交轴于点 , 连接 .
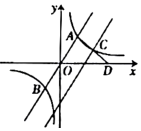
 (1)、求证是的切线;(2)、是否存在到四点 , , , 距离都相等的点?若存在,求点坐标,并写出以为圆心,以为半径的的方程;若不存在,说明理由.17. 如图1,对称轴为直线的抛物线经过、两点,抛物线与轴的另一交点为A.
(1)、求证是的切线;(2)、是否存在到四点 , , , 距离都相等的点?若存在,求点坐标,并写出以为圆心,以为半径的的方程;若不存在,说明理由.17. 如图1,对称轴为直线的抛物线经过、两点,抛物线与轴的另一交点为A. (1)、求抛物线的解析式;(2)、若点为抛物线对称轴上的一点,使取得最小值,求点的坐标;(3)、如图2,若是线段上方抛物线上一动点,过点作垂直于轴,交线段于点 , 是否存在点使线段的长度最大,如存在求出点的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、若点为抛物线对称轴上的一点,使取得最小值,求点的坐标;(3)、如图2,若是线段上方抛物线上一动点,过点作垂直于轴,交线段于点 , 是否存在点使线段的长度最大,如存在求出点的坐标;若不存在,请说明理由.三、填空题
-
18. 若式子在实数范围内有意义,则x的取值范围是 .19. 分解因式: .