山东省济宁市嘉祥县2022年中考第一次模拟数学试题
试卷更新日期:2022-04-29 类型:中考模拟
一、单选题
-
1. 在-2,0, , , 这四个数中,最大的数是( )A、-2 B、0 C、 D、2. 2022年国务院政府工作报告中提出,过去一年经济保持恢复发展,国内生产总值达到114万亿元,用科学记数法可以表示为( )A、元 B、元 C、元 D、元3. 下列等式从左到右的变形,其中属于因式分解的是( )A、 B、 C、 D、4. 如图,第24届北京冬奥会的口号“一起向未来”五个字及会微被分开印刷在一个正方体的六个面上,其平面展开图如图所示,那么在该正方体中与北京冬奥会会徽相对的字是( )
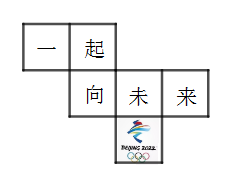 A、一 B、起 C、向 D、来5. 如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
A、一 B、起 C、向 D、来5. 如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )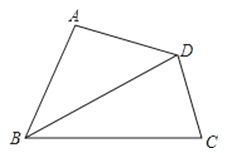 A、7.5 B、8 C、15 D、无法确定6. 为了向建党一百周年献礼,我市中小学生开展了红色经典故事演讲比赛.某参赛小组6名同学的成绩(单位:分)分别为:85,82,86,82,83,92.关于这组数据,下列说法错误的是( )A、众数是82 B、中位数是84 C、方差是84 D、平均数是857. 如图, 是半圆 的直径, , 是 上两点,连接 , 并延长交于点 ,连接 , ,如果 ,那么 的度数为( )
A、7.5 B、8 C、15 D、无法确定6. 为了向建党一百周年献礼,我市中小学生开展了红色经典故事演讲比赛.某参赛小组6名同学的成绩(单位:分)分别为:85,82,86,82,83,92.关于这组数据,下列说法错误的是( )A、众数是82 B、中位数是84 C、方差是84 D、平均数是857. 如图, 是半圆 的直径, , 是 上两点,连接 , 并延长交于点 ,连接 , ,如果 ,那么 的度数为( )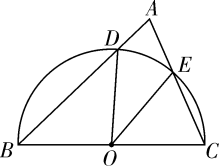 A、 B、 C、 D、8. 如果不等式组 的解集为 ,那么 的取值范围是( )A、 B、 C、 D、9. 如图,正方形ABCD的边长为3,E为BC边上一点,BE=1.将正方形沿GF折叠,使点A恰好与点E重合,连接AF , EF , GE , 则四边形AGEF的面积为( )
A、 B、 C、 D、8. 如果不等式组 的解集为 ,那么 的取值范围是( )A、 B、 C、 D、9. 如图,正方形ABCD的边长为3,E为BC边上一点,BE=1.将正方形沿GF折叠,使点A恰好与点E重合,连接AF , EF , GE , 则四边形AGEF的面积为( )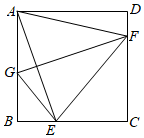 A、2 B、2 C、6 D、510. 如图,在菱形ABCD中,∠B=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿折线BA→AC运动到点C,同时动点Q从点A出发,以相同速度沿折线AC→CD运动到点D,当一个点停止运动时,另一个点也随之停止.设△APQ的面积为y,运动时间为x秒,则下列图象能大致反映y与x之间函数关系的是( )
A、2 B、2 C、6 D、510. 如图,在菱形ABCD中,∠B=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿折线BA→AC运动到点C,同时动点Q从点A出发,以相同速度沿折线AC→CD运动到点D,当一个点停止运动时,另一个点也随之停止.设△APQ的面积为y,运动时间为x秒,则下列图象能大致反映y与x之间函数关系的是( )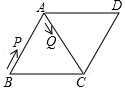 A、
A、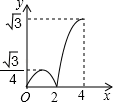 B、
B、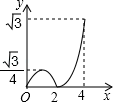 C、
C、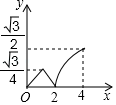 D、
D、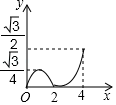
二、填空题
-
11. 估计的值在两个连续整数a和b之间,则a+b= .12. 计算的结果为 .13. 如图,在菱形 中, 是对角线, ,⊙O与边 相切于点D,则图中阴影部分的面积为 .
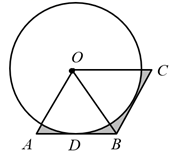 14. 如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点B'的坐标是
14. 如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点B'的坐标是 15. 观察下列各式: , , , , , , , 根据其中的规律可得 .
15. 观察下列各式: , , , , , , , 根据其中的规律可得 .三、解答题
-
16. 先化简再求值: , 其中 .17. 2019年4月23日是第二十四个“世界读书日“.某校组织读书征文比赛活动,评选出一、二、三等奖若干名,并绘成如图所示的条形统计图和扇形统计图(不完整),请你根据图中信息解答下列问题:
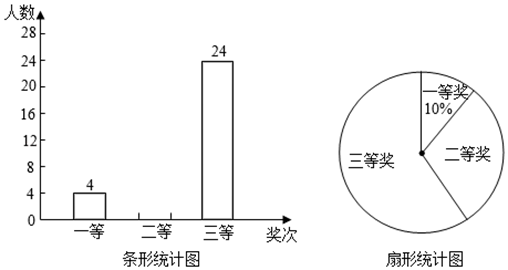 (1)、求本次比赛获奖的总人数,并补全条形统计图;(2)、求扇形统计图中“二等奖”所对应扇形的圆心角度数;(3)、学校从甲、乙、丙、丁4位一等奖获得者中随机抽取2人参加“世界读书日”宣传活动,请用列表法或画树状图的方法,求出恰好抽到甲和乙的概率.18. 如图,在△ABC中, .
(1)、求本次比赛获奖的总人数,并补全条形统计图;(2)、求扇形统计图中“二等奖”所对应扇形的圆心角度数;(3)、学校从甲、乙、丙、丁4位一等奖获得者中随机抽取2人参加“世界读书日”宣传活动,请用列表法或画树状图的方法,求出恰好抽到甲和乙的概率.18. 如图,在△ABC中, . (1)、先作AB的中点O,然后以OA为半径作 , 交AC于点D,过点D作 , 垂足为点E.(要求:尺规作图,保留作图痕迹,不写作法)(2)、若 , , 求此时DE的长.19. 某水果商店销售一种进价为40元/千克的优质水果,若售价为50元/千克,则一个月可售出500千克;若售价在50元/千克的基础上每涨价1元,则月销售量就减少10千克.(1)、当售价为55元/千克时,每月销售水果多少千克?(2)、当月利润为8750元时,每千克水果售价为多少元?(3)、当每千克水果售价为多少元时,获得的月利润最大?20. 如图,点P为函数与函数图象的交点,点P的纵坐标为4,轴,垂足为点B.
(1)、先作AB的中点O,然后以OA为半径作 , 交AC于点D,过点D作 , 垂足为点E.(要求:尺规作图,保留作图痕迹,不写作法)(2)、若 , , 求此时DE的长.19. 某水果商店销售一种进价为40元/千克的优质水果,若售价为50元/千克,则一个月可售出500千克;若售价在50元/千克的基础上每涨价1元,则月销售量就减少10千克.(1)、当售价为55元/千克时,每月销售水果多少千克?(2)、当月利润为8750元时,每千克水果售价为多少元?(3)、当每千克水果售价为多少元时,获得的月利润最大?20. 如图,点P为函数与函数图象的交点,点P的纵坐标为4,轴,垂足为点B. (1)、求m的值;(2)、点M是函数图象上一动点,过点M作于点D,若 , 求点M的坐标.21. 定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.
(1)、求m的值;(2)、点M是函数图象上一动点,过点M作于点D,若 , 求点M的坐标.21. 定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线. (1)、如图1,在△ABC中,AB=AC,AD是△ABC的角平分线,E,F分别是BD,AD上的点.求证:四边形ABEF是邻余四边形.(2)、如图2,在(1)的条件下,取EF中点M,连结DM并延长交AB于点Q,延长EF交AC于点N.若N为AC的中点,DE=2BE,QB=3,求邻余线AB的长.22. 如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A(﹣1,0),B两点,与y轴交于点C , 过点C作CD⊥y轴交抛物线于另一点D , 作DE⊥x轴,垂足为点E , 双曲线y= (x>0)经过点D , 连接MD , BD .
(1)、如图1,在△ABC中,AB=AC,AD是△ABC的角平分线,E,F分别是BD,AD上的点.求证:四边形ABEF是邻余四边形.(2)、如图2,在(1)的条件下,取EF中点M,连结DM并延长交AB于点Q,延长EF交AC于点N.若N为AC的中点,DE=2BE,QB=3,求邻余线AB的长.22. 如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A(﹣1,0),B两点,与y轴交于点C , 过点C作CD⊥y轴交抛物线于另一点D , 作DE⊥x轴,垂足为点E , 双曲线y= (x>0)经过点D , 连接MD , BD .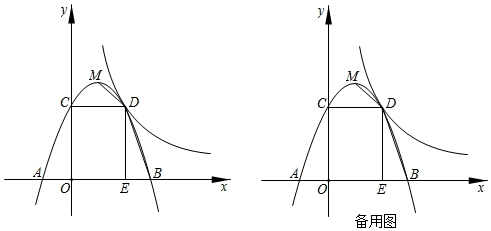 (1)、求抛物线的表达式;(2)、点N , F分别是x轴,y轴上的两点,当以M , D , N , F为顶点的四边形周长最小时,求出点N , F的坐标;(3)、动点P从点O出发,以每秒1个单位长度的速度沿OC方向运动,运动时间为t秒,当t为何值时,∠BPD的度数最大?
(1)、求抛物线的表达式;(2)、点N , F分别是x轴,y轴上的两点,当以M , D , N , F为顶点的四边形周长最小时,求出点N , F的坐标;(3)、动点P从点O出发,以每秒1个单位长度的速度沿OC方向运动,运动时间为t秒,当t为何值时,∠BPD的度数最大?