山东省德州市庆云县2022年九年级数学一练调研测试题
试卷更新日期:2022-04-29 类型:中考模拟
一、单选题
-
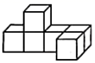
1. -7的倒数是( )A、 B、 C、-7 D、72. 如图所示的几何体是由6个大小相同的小立方块搭成,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 菲尔兹奖是数学领域的一项国际大奖,常被视为数学界的诺贝尔奖,每四年颁发一次,最近一届获奖者获奖时的年龄(单位:岁)分别为:30,40,34,36,则这组数据的中位数是( )A、34 B、35 C、36 D、405. 如图,四边形 是菱形,点E,F分别在 边上,添加以下条件不能判定 的是( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 菲尔兹奖是数学领域的一项国际大奖,常被视为数学界的诺贝尔奖,每四年颁发一次,最近一届获奖者获奖时的年龄(单位:岁)分别为:30,40,34,36,则这组数据的中位数是( )A、34 B、35 C、36 D、405. 如图,四边形 是菱形,点E,F分别在 边上,添加以下条件不能判定 的是( ) A、 B、 C、 D、6. 定义运算:例如:则方程的根的情况为( )A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、无法确定7. 如图,正六边形 的边长为6,以顶点A为圆心, 的长为半径画圆,则图中阴影部分的面积为( )
A、 B、 C、 D、6. 定义运算:例如:则方程的根的情况为( )A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、无法确定7. 如图,正六边形 的边长为6,以顶点A为圆心, 的长为半径画圆,则图中阴影部分的面积为( ) A、 B、 C、 D、8. 一次函数y=ax+c与二次函数y=ax2+bx+c在同一个平面坐标系中图象可能是( )A、
A、 B、 C、 D、8. 一次函数y=ax+c与二次函数y=ax2+bx+c在同一个平面坐标系中图象可能是( )A、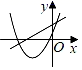 B、
B、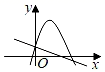 C、
C、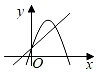 D、
D、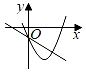 9. 如图, 是⊙O的直径,点C为圆上一点, 的平分线交 于点D , ,则⊙O的直径为( )
9. 如图, 是⊙O的直径,点C为圆上一点, 的平分线交 于点D , ,则⊙O的直径为( ) A、 B、 C、1 D、210. 在平面直角坐标系xOy中,点和点在抛物线上.已知点 , , 在该抛物线上.若 , 则 , , 的大小为( ).A、 B、 C、 D、11. 如图1,中, , 为锐角.要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案( ).
A、 B、 C、1 D、210. 在平面直角坐标系xOy中,点和点在抛物线上.已知点 , , 在该抛物线上.若 , 则 , , 的大小为( ).A、 B、 C、 D、11. 如图1,中, , 为锐角.要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案( ).
取BD中点O,作 ,
作于N,于M
作AN,CM分别平分 , , 交BD于点N,M
A、甲、乙、丙都是 B、只有甲、乙才是 C、只有甲、丙才是 D、只有乙、丙才是12. 如图,两个大小不同的正方形在同一水平线上,小正方形从图①的位置开始,匀速向右平移,到图③的位置停止运动.如果设运动时间为x,两个正方形重叠部分的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
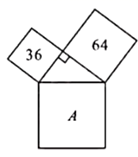
13. 计算的结果是 .14. 如图,数字代表所在正方形的面积,则A所代表的正方形的面积为.
 15. 一副三角板如图摆放,且 ,则∠1的度数为 .
15. 一副三角板如图摆放,且 ,则∠1的度数为 .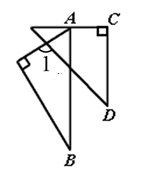 16. 端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元,某商家用8000元购进的猪肉粽和用6000元购进的豆沙粽盒数相同.则豆沙粽每盒的进价 .17. 如图,在中, , 作BC的垂直平分线交AC于点D,连接BD,若 , 则的值为 .
16. 端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元,某商家用8000元购进的猪肉粽和用6000元购进的豆沙粽盒数相同.则豆沙粽每盒的进价 .17. 如图,在中, , 作BC的垂直平分线交AC于点D,连接BD,若 , 则的值为 . 18. 正比例函数 ( )的图象与反比例函数 的图象相交于点 和点 ,点 的坐标为 ,点 是 轴正半轴上一点,连接AB、BC,作点 关于直线BC的对称点 ,现有以下结论:
18. 正比例函数 ( )的图象与反比例函数 的图象相交于点 和点 ,点 的坐标为 ,点 是 轴正半轴上一点,连接AB、BC,作点 关于直线BC的对称点 ,现有以下结论:① ;
②点 的坐标为 ;
③当 时,四边形 为菱形;
④当四边形 为菱形时,点 的坐标为 .
其中正确的是.(写出所有正确结论的序号)
三、解答题
-
19. 先化简,再求值: ,其中 .20. 为弘扬中华传统文化,某学校准备开展“传统手工技艺”学习实践活动.校学生会在全校范围内随机地对本校一些学生进行了“我最想学习的传统手工技艺”问卷调查(问卷共设有五个选项:“A——剪纸”、“B——木版画雕刻”、“C——陶艺创作”、“D——皮影制作”、“E——其他手工技艺”,参加问卷调查的这些学生,每人都只选了其中的一个选项),将所有的调查结果绘制成如下两幅不完整的统计图:

请你根据以上信息,回答下列问题:
(1)、补全上面的条形统计图;(2)、本次问卷的这五个选项中,众数是;(3)、该校共有3600名学生,请你估计该校学生“最想学习的传统手工技艺”为“A——剪纸”的人数.(4)、学校决定从选填结果是A类的学生中,选取甲、乙、丙、丁四人,从这四位学生中随机抽取两名学生参与冬奥知识竞赛,用画树状图或列表的方法,求甲、乙两名同学同时被抽中的概率.21. 如图,大楼底右侧有一障碍物,在障碍物的旁边有一栋小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=40m,DE=10m,求障碍物B,C两点间的距离,(结果保留根号) 22.
22.如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C.
 (1)、求证:PB是⊙O的切线;(2)、连接OP,若OP∥BC,且OP=8,⊙O的半径为2 , 求BC的长.23. 中共中央办公厅、国务院办公厅印发《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》.某学校积极响应“双减”政策,为了丰富学生校园生活,经研究决定准备购头一批体育健身器材,已知购买2个篮球和3个排球共花费440元,购买4个篮球和1个排球共花费480元.(1)、求篮球和排球的单价;(2)、某体育用品店有两种优惠方案,
(1)、求证:PB是⊙O的切线;(2)、连接OP,若OP∥BC,且OP=8,⊙O的半径为2 , 求BC的长.23. 中共中央办公厅、国务院办公厅印发《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》.某学校积极响应“双减”政策,为了丰富学生校园生活,经研究决定准备购头一批体育健身器材,已知购买2个篮球和3个排球共花费440元,购买4个篮球和1个排球共花费480元.(1)、求篮球和排球的单价;(2)、某体育用品店有两种优惠方案,方案一:每购买一个篮球就送一个排球;
方案二:购买篮球和排球的费用一律打七五折,该学校需要购买40个篮球和x个排球 .
方案一的费用为元,方案二的费用为元.
①根据题目信息,直接写出与x的的函数表达式 ▲ ;与x的函数表达式 ▲ ;
②请根据购买排球的数量x设计一种比较省钱的购买方案.
24. 如图,在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm,现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿CB向点B方向运动,如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求: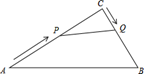 (1)、当t=3秒时,这时,P,Q两点之间的距离是多少?(2)、若△CPQ的面积为S,求S关于t的函数关系式.(3)、当t为多少秒时,以点C,P,Q为顶点的三角形与△ABC相似?25. 如图,在平面直角坐标系中,抛物线经过点 , 点 , 点 , 点为抛物线L上任意一点.
(1)、当t=3秒时,这时,P,Q两点之间的距离是多少?(2)、若△CPQ的面积为S,求S关于t的函数关系式.(3)、当t为多少秒时,以点C,P,Q为顶点的三角形与△ABC相似?25. 如图,在平面直角坐标系中,抛物线经过点 , 点 , 点 , 点为抛物线L上任意一点. (1)、求抛物线L的解析式;(2)、当时,求n的最大值和最小值;(3)、过点P作轴,点Q的横坐标为 . 已知点P与点Q不重合.
(1)、求抛物线L的解析式;(2)、当时,求n的最大值和最小值;(3)、过点P作轴,点Q的横坐标为 . 已知点P与点Q不重合.①求线段PQ的长;(用含m的代数式表示)
②当时,直接写出线段PQ与抛物线的图象只有一个交点时m的取值范围.