陕西省2022年中考数学摸底调研试卷
试卷更新日期：2022-04-29 类型：中考模拟
一、单选题
-
1. -3的倒数是（ ）A、 B、 C、 D、-32. 如图所示的几何体的俯视图是（ ）
A、
B、
C、
D、
3. 计算（ ab2）3的结果是（ ）A、 a3b6 B、 a3b5 C、 a3b6 D、 a3b64. 如图，在△ABC中，∠C＝36°，将△ABC绕点A逆时针旋转60°得到△AED，AD与BC交于点F，则∠AFC的度数为（ ）
A、72° B、74° C、84° D、86°5. 如图，▱ABCD中，点E是AD的中点，EC交对角线BD于点F，则 （ ）
A、 B、2 C、 D、6. 已知点A（﹣3，﹣2）沿水平方向向右平移4个单位长度得到点A'.若点A'在直线y＝x+b上，则b的值为（ ）A、5 B、3 C、1 D、﹣37. 如图，在矩形ABCD中，对角线AC与BD相交于点O，E，F分别为AO，AD的中点.若AB＝6cm，BC＝8cm，则EF的长为（ ）
A、4cm B、3cm C、 cm D、2cm8. 已知抛物线y＝﹣2x2+bx+c与x轴只有一个交点，且过点A（m﹣4，n），B（m+2，n），则n的值为（ ）A、﹣18 B、﹣16 C、﹣12 D、18二、填空题
-
9. 比较大小：－4－ .（填“＞”、“＜”或“＝”）10. 如图，正五边形ABCDE内接于⊙O，则∠ADE的度数是 .
11. 已知关于x的一元二次方程mx2﹣4x+2＝0有两个不相等的实数根，则m的取值范围是 .12. 如图，原点O是矩形ABCD的对称中心，顶点A、C在反比例函数图象上，AB//x轴，若S矩形ABCD＝8，则反比例函数的表达式为 .
13. 如图，在正方形ABCD中，点E，F分别在边BC、CD上，连接AE，BF.若AB ，BE＝DF，则AE+BF的最小值为 .
三、解答题
-
14. 计算： （π﹣2022）0﹣2cos30°.15. 解不等式组： .16. 先化简，再求值：（1 ） ，其中x＝﹣3.17. 如图，在 中，点 为 边的中点，请用尺规在 边上求作点 ，使得 .（保留作图痕迹，不写作法）
18. 已知：如图，点D在△ABC的BC边上，AC∥BE，BC=BE，∠ABC=∠E，求证：AB=DE．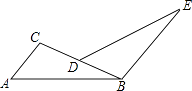
19. 2021年“房住不炒”第三次出现在政府报告中，明确了要稳地价，稳房价、稳预期.为响应中央“房住不炒”的基本政策，某房企连续降价两次后的平均价格比降价之前减少了19%，求平均每次降价的百分率.20. 2022年冬奥会在北京和张家口联合举办.乐乐和果果都计划去观看冬奥项目比赛.他们都喜欢的冬奥项目分别是：A.花样滑冰，B.速度滑冰，C.跳台滑雪，D.自由式滑雪.乐乐和果果计划各自在这4个冬奥项目中任意选择一个观看，每个项目被选择的可能性相同.(1)、乐乐选择项目“A.花样滑冰”的概率是；(2)、用画树状图或列表的方法，求乐乐和果果恰好选择同一项目观看的概率.21. 为保护师生健康，新都某中学在学校门口安装了红外测温通道，对进校师生进行体温监测，测温装置安装在E处.某同学进校时，当他在地面D处，开始显示测量体温，此时在其额头A处测得E的仰角为 ，当他走到地面C处，结束显示体温，此时在其额头B处测得E的仰角为 ，已知该同学脚到额头的高度为 ，且 米， 米，求测温装置E距地面的高度约为多少米？（保留小数点后两位有效数字， ）
22. 为了响应国家“美丽中国，我是行动者”提升公民生态文明意识行动计划（2021～2025），某校举办了以“生态文明，从我做起”为主题的知识竞赛，满分10分，学生得分为整数，成绩达到8分以上（包括8分）为优秀.如图是该校九（1）班学生成绩分布的条形统计图和扇形统计图.
根据以上信息，解答下列问题：
(1)、九（1）班的总人数是▲ 人，并补全条形统计图；(2)、九（1）班学生成绩的众数是分，中位数是分；(3)、求该班平均成绩是多少分？23. 甲、乙两地相距300km，一辆货车和一辆轿车先后从甲地出发开向乙地.如图，线段OA表示货车离甲地距离y（km）与时间x（h）之间的函数关系；折线BCD表示轿车离甲地距离y（km）与x（h）之间的函数关系.
请根据图象，解答下列问题：
(1)、求线段CD对应的函数表达式；(2)、求货车从甲地出发后多长时间与轿车相遇？24. 如图，以BC为直径的⊙O交△ABC的边AB于点D，过点D作⊙O的切线交AC于点E，且AC＝BC.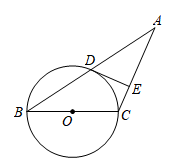
(1)、求证：DE⊥AC；(2)、若BC＝4cm，AD＝3cm，求AE的长.25. 如图，抛物线y＝x2+bx+c与x轴交于A（1，0），B两点，与y轴交于点C（0，3）.
(1)、求该抛物线的表达式；(2)、过点B作x轴的垂线，在该垂线上取一点P，使得△PBC与△ABC相似，请求出点P的坐标.26. 问题提出：
(1)、如图①，在矩形ABCD内，以BC的中点O为圆心，BC为直径作半圆，Q为半圆上一点.若AB=6，BC=8，求△ADQ的面积的最小值；(2)、问题解决：
如图2，矩形ABCD是城区改造过程中的一块闲置空地，AB=300m，BC=400m，E是AB边上一点，AE=200m，F是BC边上的任意一点.为了美化环境，市规划办决定修建AG、CG、EG、FG四条小路，并在四边形AGCD围成的区域种植草坪，△AEG，△GFC围成的区域种植鲜花，△BEF围成的区域修建供市民休息的凉亭，△GEF围成的区域投放健身器材，供市民锻炼身体，且△BEF与△GEF关于EF成轴对称.根据以上所给信息，求出草坪AGCD面积的最小值.