江苏省南通市海门区2022年中考模拟数学试卷
试卷更新日期:2022-04-29 类型:中考模拟
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 345万这个数用科学记数法表示为( )A、 0.345×107 B、3.45×106 C、34.5×105 D、345×1043. 下列水平放置的几何体中,俯视图是矩形的是( )A、圆柱
 B、长方体
B、长方体 C、三棱柱
C、三棱柱  D、圆锥
D、圆锥 4. 不等式 的解集在数轴上表示正确的是( )A、
4. 不等式 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 下列运算,正确的是( )A、 B、 C、 D、6. 将一副三角尺按如图的方式摆放,其中l1∥l2 , 则∠α的度数是( )
5. 下列运算,正确的是( )A、 B、 C、 D、6. 将一副三角尺按如图的方式摆放,其中l1∥l2 , 则∠α的度数是( ) A、30° B、45° C、60° D、70°7. 已知平行四边形 的对角线相交于点 ,补充下列四个条件,能使平行四边形 成为菱形的是( )
A、30° B、45° C、60° D、70°7. 已知平行四边形 的对角线相交于点 ,补充下列四个条件,能使平行四边形 成为菱形的是( )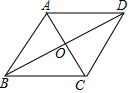 A、 B、 C、 D、8. 某商店今年1月份的销售额是1万元,3月份的销售额是1.21万元,从1月份到3月份,该店销售额平均每月的增长率是( )A、20% B、15% C、10% D、5%9. 为说明命题“若m>n,则m2>n2”是假命题,所列举反例正确的是( )A、m=6,n=3 B、m=0.2,n=0.01 C、m=1,n=﹣6 D、m=0.5,n=0.310. 如图,菱形 的边长为 是边 的中点,F是边 上的一个动点,将线段 绕着E逆时针旋转 ,得到 ,连接 ,则 的最小值为( )
A、 B、 C、 D、8. 某商店今年1月份的销售额是1万元,3月份的销售额是1.21万元,从1月份到3月份,该店销售额平均每月的增长率是( )A、20% B、15% C、10% D、5%9. 为说明命题“若m>n,则m2>n2”是假命题,所列举反例正确的是( )A、m=6,n=3 B、m=0.2,n=0.01 C、m=1,n=﹣6 D、m=0.5,n=0.310. 如图,菱形 的边长为 是边 的中点,F是边 上的一个动点,将线段 绕着E逆时针旋转 ,得到 ,连接 ,则 的最小值为( )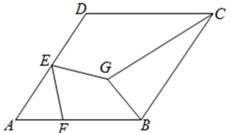 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式:2x2-8y2=.12. 计算( - )× 的结果是 .13. AB是⊙O的弦,OM⊥AB,垂足为M,连接OA.若△AOM中有一个角是60°,OM= ,则弦AB的长为.14. 如图,扇形的弧长是 ,面积是 ,则此扇形的圆心角的度数是.
 15. 已知α,β是方程 的两实根,则 的值为.16. 已知关于x的一元二次方程 有两个实数根 , ,若 , 满足 ,则m的值为17. 设方程x2﹣4x+1=0的两个根为x1与x2 , 则x1+x2﹣x1x2的值是.18. 已知关于x的二次函数y=ax2+(a2﹣1)x﹣a的图象与x轴的一个交点的坐标为(m,0).若2<m<3,则a的取值范围是 .
15. 已知α,β是方程 的两实根,则 的值为.16. 已知关于x的一元二次方程 有两个实数根 , ,若 , 满足 ,则m的值为17. 设方程x2﹣4x+1=0的两个根为x1与x2 , 则x1+x2﹣x1x2的值是.18. 已知关于x的二次函数y=ax2+(a2﹣1)x﹣a的图象与x轴的一个交点的坐标为(m,0).若2<m<3,则a的取值范围是 .三、解答题
-
19. 解方程组(1)、(2)、20. 2019年12月以来,湖北省武汉市部分医院陆续发现不明原因肺炎病例,现已证实该肺炎为一种新型冠状病毒感染的肺炎,其传染性较强.为了有效地避免交叉感染,需要采取以下防护措施:①戴口罩;②勤洗手;③少出门;④重隔离;⑤捂口鼻;⑥谨慎吃.某公司为了解员工对防护措施的了解程度(包括不了解、了解很少、基本了解和很了解),通过网上问卷调查的方式进行了随机抽样调查(每名员工必须且只能选择一项),并将调查结果绘制成如下两幅统计图.请你根据信息,解答下列问题:
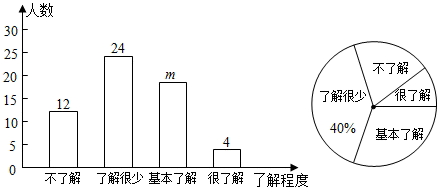 (1)、本次共调查了名员工,条形统计图中m=;(2)、若该公司共有员工1000名,请你估计“不了解”防护措施的人数;(3)、在调查中,发现有4名员工对防护措施“很了解”,其中有3名男员工、1名女员工.若准备从他们中随机抽取2名,让其在公司群内普及防护措施,用画树状图或列表法求恰好抽中一男一女的概率(要求画出树状图或列出表格).21. 端午节那天,小贤回家看到桌上有一盘粽子,其中有豆沙粽、肉粽各1个,蜜枣粽2个,这些粽子除馅外无其他差别.(1)、小贤随机地从盘中取出一个粽子,取出的是肉粽的概率是多少?(2)、小贤随机地从盘中取出两个粽子,试用画树状图或列表的方法表示所有可能的结果,并求出小贤取出蜜枣粽的概率.22. 某工厂甲、乙两个部门各有员工400人,为了了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
(1)、本次共调查了名员工,条形统计图中m=;(2)、若该公司共有员工1000名,请你估计“不了解”防护措施的人数;(3)、在调查中,发现有4名员工对防护措施“很了解”,其中有3名男员工、1名女员工.若准备从他们中随机抽取2名,让其在公司群内普及防护措施,用画树状图或列表法求恰好抽中一男一女的概率(要求画出树状图或列出表格).21. 端午节那天,小贤回家看到桌上有一盘粽子,其中有豆沙粽、肉粽各1个,蜜枣粽2个,这些粽子除馅外无其他差别.(1)、小贤随机地从盘中取出一个粽子,取出的是肉粽的概率是多少?(2)、小贤随机地从盘中取出两个粽子,试用画树状图或列表的方法表示所有可能的结果,并求出小贤取出蜜枣粽的概率.22. 某工厂甲、乙两个部门各有员工400人,为了了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.收集数据从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如表:
甲
78
86
74
81
75
76
87
70
75
90
75
79
81
70
74
80
86
69
83
77
乙
93
73
88
81
72
81
94
83
77
83
80
81
70
81
73
78
82
80
70
40
整理、描述数据按如下分数段整理、描述这两组样本数据:
成绩x人数
部门
40≤x≤49
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
甲
0
0
1
11
7
1
乙
1
0
0
7
10
2
(说明:成绩80分及以上为生产技能优秀,70~79分为生产技能良好,60~69分为生产技能合格,60分以下为生产技能不合格)
分析数据两组样本数据的平均数、中位数、众数如表所示:
部门
平均数
中位数
众数
方差
甲
78.3
77.5
m
33.61
乙
78
n
81
117.5
得出结论
(1)、上表中m= , n=;(2)、甲、乙两个部门员工的生产技能水平比较均衡的是部门,估计乙部门生产技能优秀的员工人数为;(3)、可以推断出部门员工的生产技能水平较高,理由为.(至少从两个不同的角度说明推断的合理性)23. 如图,已知⊙O的直径AB=12,弦AC=10,D是 的中点,过点D作DE⊥AC,交AC的延长线于点E. (1)、求证:DE是⊙O的切线;(2)、求AE的长.24. 元旦期间,小黄自驾游去了离家156千米的黄石矿博园,右图是小黄离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
(1)、求证:DE是⊙O的切线;(2)、求AE的长.24. 元旦期间,小黄自驾游去了离家156千米的黄石矿博园,右图是小黄离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象. (1)、求小黄出发0.5小时时,离家的距离;(2)、求出AB段的图象的函数解析式;(3)、小黄出发1.5小时时,离目的地还有多少千米?25. 已知关于x的方程ax2+(3a+1)x+3=0.(1)、求证:无论a取任何实数时,该方程总有实数根;(2)、若抛物线y=ax2+(3a+1)x+3的图象与x轴两个交点的横坐标均为整数,且a为正整数,求a值以及此时抛物线的顶点H的坐标;(3)、在(2)的条件下,直线y=﹣x+5与y轴交于点C,与直线OH交于点D.现将抛物线平移,保持顶点在直线OD上.若平移的抛物线与射线CD(含端点C)只有一个公共点,请直接写出它的顶点横坐标h的值或取值范围.26. 在平面直角坐标系xOy中,⊙O的半径为1
(1)、求小黄出发0.5小时时,离家的距离;(2)、求出AB段的图象的函数解析式;(3)、小黄出发1.5小时时,离目的地还有多少千米?25. 已知关于x的方程ax2+(3a+1)x+3=0.(1)、求证:无论a取任何实数时,该方程总有实数根;(2)、若抛物线y=ax2+(3a+1)x+3的图象与x轴两个交点的横坐标均为整数,且a为正整数,求a值以及此时抛物线的顶点H的坐标;(3)、在(2)的条件下,直线y=﹣x+5与y轴交于点C,与直线OH交于点D.现将抛物线平移,保持顶点在直线OD上.若平移的抛物线与射线CD(含端点C)只有一个公共点,请直接写出它的顶点横坐标h的值或取值范围.26. 在平面直角坐标系xOy中,⊙O的半径为1给出如下定义:记线段AB的中点为M ,当点M不在⊙O上时,平移线段AB,使点M落在⊙O上,得到线段A′B′(A′,B′分别为点A,B的对应点).线段AA'长度的最小值称为线段AB到⊙O的“平移距离”.
 (1)、已知点A的坐标为(-1,0),点B在x轴上.
(1)、已知点A的坐标为(-1,0),点B在x轴上.①若点B与原点O重合,则线段AB到⊙O的“平移距离”为;
②若线段AB到⊙O的“平移距离”为2,则点B的坐标为;
(2)、若点A,B都在直线 上,AB=2,记线段AB到⊙O的“平移距离”为d1 , 求d1最小值;(3)、若点A的坐标为(3,4),AB=2,记线段AB到⊙O的“平移距离”为d2 , 直接写出d2的取值范围.