江苏省无锡市惠山区八校2022年九年级3月阶段性检测(中考一模)数学试卷
试卷更新日期:2022-04-29 类型:中考模拟
一、单选题
-
1. 4的相反数是( )A、-4 B、4 C、±4 D、2. 已知一次函数y=kx+3的图象与x轴交于点A(3,0),则k的值为( )A、1 B、3 C、-1 D、-33. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图,左图是由4个大小相同的正方体组合而成的几何体,其主视图是( )
4. 如图,左图是由4个大小相同的正方体组合而成的几何体,其主视图是( )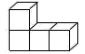 A、
A、 B、
B、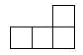 C、
C、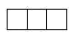 D、
D、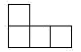 5. 下列运算正确的是( )A、a2+a=a3 B、(a2)3=a5 C、a8÷a2=a4 D、a2•a3=a56. 下列命题中,是真命题的是 ( )A、长度相等的弧是等弧 B、如果|a|=1,那么a=1 C、两直线平行,同位角相等 D、如果x>y ,那么-2x>-2y7. 下列说法中,正确的是( )A、为检测一批灯泡的质量,应该采用普查的方式 B、若两名同学连续五次数学测试的平均分相同,则方差较大的同学数学成绩更稳定 C、抛掷一枚均匀的硬币,正面朝上的概率是 D、“打开电视,正在播放广告”是必然事件8. 随着“互联网+”时代的到来,一种新型的打车方式受到大众欢迎.打车总费用y(单位:元)与行驶里程x(单位:千米)的函数关系如图所示.如果小明某次打车行驶里程为22千米,则他的打车费用为( )
5. 下列运算正确的是( )A、a2+a=a3 B、(a2)3=a5 C、a8÷a2=a4 D、a2•a3=a56. 下列命题中,是真命题的是 ( )A、长度相等的弧是等弧 B、如果|a|=1,那么a=1 C、两直线平行,同位角相等 D、如果x>y ,那么-2x>-2y7. 下列说法中,正确的是( )A、为检测一批灯泡的质量,应该采用普查的方式 B、若两名同学连续五次数学测试的平均分相同,则方差较大的同学数学成绩更稳定 C、抛掷一枚均匀的硬币,正面朝上的概率是 D、“打开电视,正在播放广告”是必然事件8. 随着“互联网+”时代的到来,一种新型的打车方式受到大众欢迎.打车总费用y(单位:元)与行驶里程x(单位:千米)的函数关系如图所示.如果小明某次打车行驶里程为22千米,则他的打车费用为( ) A、33元 B、36元 C、40元 D、42元9. 如图,在△ABC中,∠BAC=30°,AC=4,动点E从点A出发沿射线AB运动,连接CE,将CE绕点C顺时针旋转30°得到CF,连接AF,则△AFC的面积变化情况是( )
A、33元 B、36元 C、40元 D、42元9. 如图,在△ABC中,∠BAC=30°,AC=4,动点E从点A出发沿射线AB运动,连接CE,将CE绕点C顺时针旋转30°得到CF,连接AF,则△AFC的面积变化情况是( )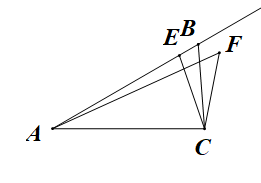 A、先变大再变小 B、先变小再变大 C、逐渐变大 D、不变10. 如图,在平面直角坐标系中,A(0,3)、B(3,0),以点B为圆心、2为半径的⊙B上有一动点P.连接AP,若点C为AP的中点,连接OC,则OC的最小值为( )
A、先变大再变小 B、先变小再变大 C、逐渐变大 D、不变10. 如图,在平面直角坐标系中,A(0,3)、B(3,0),以点B为圆心、2为半径的⊙B上有一动点P.连接AP,若点C为AP的中点,连接OC,则OC的最小值为( )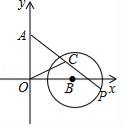 A、1 B、2﹣1 C、 D、﹣1
A、1 B、2﹣1 C、 D、﹣1二、填空题
-
11. 若分式 有意义,则 的取值范围是.12. 分解因式: -9= .13. 2021年某超市年收入总值约15000元,将15000元这个数据用科学记数法表示为元.14. 已知圆锥的底面半径为4cm,母线长为5cm,则圆锥的侧面积是15. 一组数6,7,6,5,5,7的平均数为 , 中位数为16. 如图,抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),B(3,q)两点,则不等式ax2+c<mx+n的解集是.
 17. 如图,D、E分别是△ABC的边AB、AC上的点,且 , BE、CD相交于点O,若S△DOE:S△EOC=1:3,则当S△ADE=1时,四边形DBCE的面积是.
17. 如图,D、E分别是△ABC的边AB、AC上的点,且 , BE、CD相交于点O,若S△DOE:S△EOC=1:3,则当S△ADE=1时,四边形DBCE的面积是. 18. 已知点P(x,y)在以原点为圆心,半径为5的圆上运动,则3x+4y的最大值为.
18. 已知点P(x,y)在以原点为圆心,半径为5的圆上运动,则3x+4y的最大值为.三、解答题
-
19. 计算:(1)、3tan45°-(π-1)0+ ;(2)、(a+b)2-(a+b)(a-b).20.(1)、解方程:x(x-2)=8;(2)、解不等式21. 如图,AB=AC,AD=AE,∠BAC=∠DAE.
 (1)、求证:△ABD≌△ACE;(2)、若∠1=25°,∠2=30°,求∠3的度数.22. 目前,我国的空气质量得到了大幅度的提高.现随机调查了某城市1个月的空气质量情况,并将监测的结果绘制成如下的两幅不完整的统计图.
(1)、求证:△ABD≌△ACE;(2)、若∠1=25°,∠2=30°,求∠3的度数.22. 目前,我国的空气质量得到了大幅度的提高.现随机调查了某城市1个月的空气质量情况,并将监测的结果绘制成如下的两幅不完整的统计图.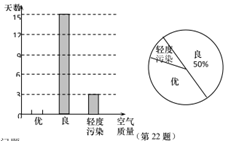
请根据图中提供的信息,解答下面的问题:
(1)、本次调查中,一共调查的天数为天;扇形图中,表示“轻度污染”的扇形的圆心角为度;(2)、将条形图补充完整;(3)、估计该城市一年(以365天计算)中,空气质量未达到优的天数.23. 2022春开学,为防控新冠病毒,学生进校必须戴口罩,测体温,某校开通了A、B、C三条人工测体温的通道,在三个通道中,可随机选择其中的一个通过.(1)、其中一个学生进校园时,由A通道过的概率是;(2)、求两学生进校园时,都是C通道过的概率.(用画“树状图”或“列表格”)24. 如图,已知点M在直线l外,点N在直线l上,请用无刻度的直尺和圆规完成下列作图,要求保留痕迹,不写作法. (1)、在图①中,以线段MN为一条对角线作菱形MPNQ,使菱形的边PN落在直线l上(2)、在图②中,做圆O,使圆O过点M,且与直线l相切于N.25. 如图所示,在中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.
(1)、在图①中,以线段MN为一条对角线作菱形MPNQ,使菱形的边PN落在直线l上(2)、在图②中,做圆O,使圆O过点M,且与直线l相切于N.25. 如图所示,在中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.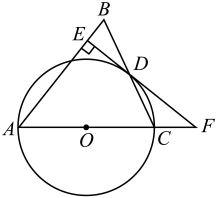 (1)、求证:EF是⊙O的切线.(2)、若EB=6,且sin∠CFD= , 求⊙O的半径与线段AE的长.26. 无锡水蜜桃享誉海内外,老王用3000元购进了一批水蜜桃.第一天,很快以比进价高40% 的价格卖出150千克.第二天,他发现剩余的水蜜桃卖相已不太好,于是果断地以比进价低20%的价格将剩余的水蜜桃全部售出,本次生意老王一共获利750元.(1)、求这批水蜜桃进价为多少元?(2)、老王用3000元按第一次的价格又购进了一批水蜜桃.第一天同样以比进价高40% 的价格卖出150千克,第二天,老王把卖相不好的水蜜桃挑出,单独打折销售,售价为10元/千克,结果很快被一抢而空,其余的仍按第一天的价格销售,且当天全部售完.若老王这次至少获利1000元,请问打折销售的水蜜桃最多多少千克?(精确到1千克.)27. 如图,抛物线 交x轴于A、B两点(点A在点B的左侧), .
(1)、求证:EF是⊙O的切线.(2)、若EB=6,且sin∠CFD= , 求⊙O的半径与线段AE的长.26. 无锡水蜜桃享誉海内外,老王用3000元购进了一批水蜜桃.第一天,很快以比进价高40% 的价格卖出150千克.第二天,他发现剩余的水蜜桃卖相已不太好,于是果断地以比进价低20%的价格将剩余的水蜜桃全部售出,本次生意老王一共获利750元.(1)、求这批水蜜桃进价为多少元?(2)、老王用3000元按第一次的价格又购进了一批水蜜桃.第一天同样以比进价高40% 的价格卖出150千克,第二天,老王把卖相不好的水蜜桃挑出,单独打折销售,售价为10元/千克,结果很快被一抢而空,其余的仍按第一天的价格销售,且当天全部售完.若老王这次至少获利1000元,请问打折销售的水蜜桃最多多少千克?(精确到1千克.)27. 如图,抛物线 交x轴于A、B两点(点A在点B的左侧), .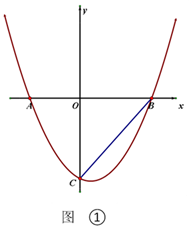
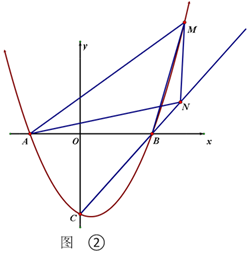 (1)、求抛物线的函数表达式;(2)、如图①,连接BC,点P在抛物线上,且∠BCO= ∠PBA.求点P的坐标(3)、如图②,M是抛物线上一点,N为射线CB上的一点,且M、N两点均在第一象限内,B、N是位于直线AM同侧的不同两点, ,点M到 轴的距离为2L,△AMN的面积为5L,且∠ANB=∠MBN,请问MN的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.28. 如图,在平面直角坐标系中,点P的坐标为(a、b),且a、b满足a2+4a+4= , 点B为x轴上动点,过点P作PC⊥y轴于点C.
(1)、求抛物线的函数表达式;(2)、如图①,连接BC,点P在抛物线上,且∠BCO= ∠PBA.求点P的坐标(3)、如图②,M是抛物线上一点,N为射线CB上的一点,且M、N两点均在第一象限内,B、N是位于直线AM同侧的不同两点, ,点M到 轴的距离为2L,△AMN的面积为5L,且∠ANB=∠MBN,请问MN的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.28. 如图,在平面直角坐标系中,点P的坐标为(a、b),且a、b满足a2+4a+4= , 点B为x轴上动点,过点P作PC⊥y轴于点C.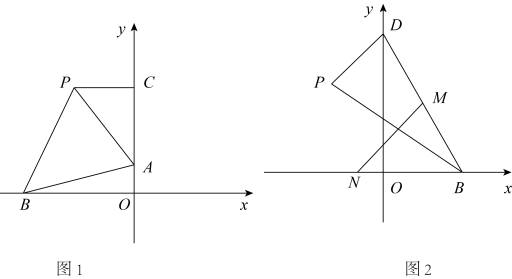 (1)、求O、P两点间的距离;(2)、如图1,点A为y轴正半轴上一点,连接PA、PB、AB,若B(﹣4,0),且2∠APB=90°+∠PAC,求点A的坐标;(3)、如图2,过点P作PD⊥PB交y轴正半轴于点D,点M为BD的中点,点N(﹣1,0),则MN的最小值为(请直接写出结果).
(1)、求O、P两点间的距离;(2)、如图1,点A为y轴正半轴上一点,连接PA、PB、AB,若B(﹣4,0),且2∠APB=90°+∠PAC,求点A的坐标;(3)、如图2,过点P作PD⊥PB交y轴正半轴于点D,点M为BD的中点,点N(﹣1,0),则MN的最小值为(请直接写出结果).