江苏省南通市2022年九年级数学中考模拟试卷
试卷更新日期:2022-04-29 类型:中考模拟
一、单选题
-
1. 在﹣ ,﹣ ,0,1四个数中,最大的数是( )A、1 B、0 C、﹣ D、﹣2. 我国探月工程嫦娥四号任务“鹊桥”中继星是世界首颗运行在地月点轨道的卫星,它的运行轨道距月球约65000公里,将65000用科学记数法表示应为( )A、 B、 C、 D、3. 若|x|=2,|y|=3,则x+y的值是( )A、5或﹣5 B、1或﹣1 C、5或1 D、5,﹣5,1,﹣14. 计算的结果是( )A、 B、 C、 D、5. 不等式组 的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、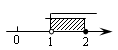 D、
D、 6. 已知m,n是一元二次方程 的两个实数根,则代数式 的值等于( )A、2019 B、2020 C、2021 D、20227. 肆虐的冠状病毒肺炎具有人传人性,调查发现:1人感染病毒后如果不隔离,那么经过两轮传染将累计会有225人感染(225人可以理解为三轮感染的总人数),若设1人平均感染x人,依题意可列方程( ).A、1+x=225 B、1+x2=225 C、(1+x)2=225 D、1+(1+x2)=2258. 如图,在正方形网格中有△ABC,△ABC绕O点按逆时针旋转90°后的图案应该是( )A、
6. 已知m,n是一元二次方程 的两个实数根,则代数式 的值等于( )A、2019 B、2020 C、2021 D、20227. 肆虐的冠状病毒肺炎具有人传人性,调查发现:1人感染病毒后如果不隔离,那么经过两轮传染将累计会有225人感染(225人可以理解为三轮感染的总人数),若设1人平均感染x人,依题意可列方程( ).A、1+x=225 B、1+x2=225 C、(1+x)2=225 D、1+(1+x2)=2258. 如图,在正方形网格中有△ABC,△ABC绕O点按逆时针旋转90°后的图案应该是( )A、 B、
B、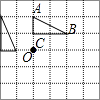 C、
C、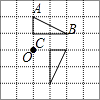 D、
D、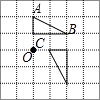 9. 如图,边长为2的正方形ABCD,点P从点A出发以每秒1个单位长度的速度沿A-D-C的路径向点C运动,同时点Q从点B出发以每秒2个单位长度的速度沿B-C-D-A的路径向点A运动,当Q到达终点时,P停止移动,设PQC的面积为S,运动时间为t秒,则能大致反映S与t的函数关系的图象是( )
9. 如图,边长为2的正方形ABCD,点P从点A出发以每秒1个单位长度的速度沿A-D-C的路径向点C运动,同时点Q从点B出发以每秒2个单位长度的速度沿B-C-D-A的路径向点A运动,当Q到达终点时,P停止移动,设PQC的面积为S,运动时间为t秒,则能大致反映S与t的函数关系的图象是( )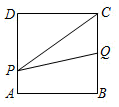 A、
A、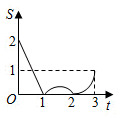 B、
B、 C、
C、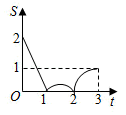 D、
D、 10. 如图,在正方形 外侧作直线 ,点C关于直线 的对称点为M,连接 , .其中 交直线 于点N.若 ,则当 时,正方形 的边长为( )
10. 如图,在正方形 外侧作直线 ,点C关于直线 的对称点为M,连接 , .其中 交直线 于点N.若 ,则当 时,正方形 的边长为( ) A、 B、5 C、 D、
A、 B、5 C、 D、二、填空题
-
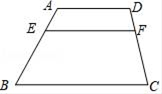
11. 计算: -1= .12. =.13. 如图,在梯形ABCD中,点E、F分别是腰AB、CD上的点,AD∥EF∥BC , 如果AD:EF:BC=5:6:9,那么 = .
 14. 如图,在矩形ABCD中,BC=3CD= ,点P是AD的中点,点E在BC上,CE=2BE,点M、N在线段BD上.若 PMN是等腰三角形且底角与∠DEC相等,则PN=.
14. 如图,在矩形ABCD中,BC=3CD= ,点P是AD的中点,点E在BC上,CE=2BE,点M、N在线段BD上.若 PMN是等腰三角形且底角与∠DEC相等,则PN=.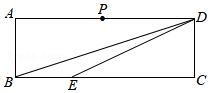 15. 已知 ,则 . .16. 已知代数式 可以利用完全平方公式变形为 , 进而可知 的最小值是 4.依此方法,代数式 的最小值是.17. 如图,点为直线上的两点,过两点分别作y轴的平行线交双曲线()于两点. 若 , 则 的值为
15. 已知 ,则 . .16. 已知代数式 可以利用完全平方公式变形为 , 进而可知 的最小值是 4.依此方法,代数式 的最小值是.17. 如图,点为直线上的两点,过两点分别作y轴的平行线交双曲线()于两点. 若 , 则 的值为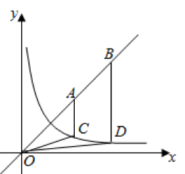 18. 平面直角坐标系xOy中,若P(m,m2+4m+3),Q(2n,4n﹣8)是两个动点(m,n为实数),则PQ长度的最小值为.
18. 平面直角坐标系xOy中,若P(m,m2+4m+3),Q(2n,4n﹣8)是两个动点(m,n为实数),则PQ长度的最小值为.三、解答题
-
19. 计算:(1)、 ;(2)、 .20. 先化简,再求值: .21. 如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E.
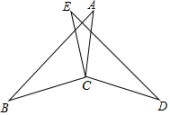 (1)、求证:BC=DC;(2)、若∠A=25°,∠D=15°,求∠ACB的度数.22. 如图,点D、A、C在同一直线上,AB∥CE,AB=CD,∠B=∠D,求证:BC=DE.
(1)、求证:BC=DC;(2)、若∠A=25°,∠D=15°,求∠ACB的度数.22. 如图,点D、A、C在同一直线上,AB∥CE,AB=CD,∠B=∠D,求证:BC=DE. 23. 2020年是脱贫攻坚的收官之年,某县的扶贫项目“小木耳,大产业”一时红遍全国.王林及家人为了助力扶贫攻坚,打算去参观该县的“木耳产业园”,并购买新鲜木耳.经了解,进园参观费每人20元,购买新鲜的木耳在2千克以内,每千克70元;超过2千克的,超过部分每千克60元,设王林和爸爸妈妈一家三口进入该木耳产业园参观并购买新鲜的木耳x千克,共付费y元.(1)、求y与x之间的函数关系式;(2)、若王林一家共付费416元,则王林一家共购买了多少千克木耳?24. 如图,在矩形ABCD中,AB=6,BC=8,点E是AD边上的动点,将矩形ABCD沿BE折叠,点A落在点 处,连接 、BD.
23. 2020年是脱贫攻坚的收官之年,某县的扶贫项目“小木耳,大产业”一时红遍全国.王林及家人为了助力扶贫攻坚,打算去参观该县的“木耳产业园”,并购买新鲜木耳.经了解,进园参观费每人20元,购买新鲜的木耳在2千克以内,每千克70元;超过2千克的,超过部分每千克60元,设王林和爸爸妈妈一家三口进入该木耳产业园参观并购买新鲜的木耳x千克,共付费y元.(1)、求y与x之间的函数关系式;(2)、若王林一家共付费416元,则王林一家共购买了多少千克木耳?24. 如图,在矩形ABCD中,AB=6,BC=8,点E是AD边上的动点,将矩形ABCD沿BE折叠,点A落在点 处,连接 、BD.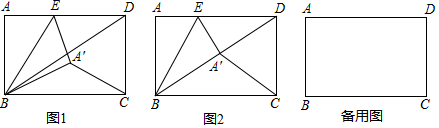 (1)、如图1,求证:∠DE =2∠ABE;(2)、如图2,若点 恰好落在BD上,求tan∠ABE的值;(3)、若AE=2,求 .(4)、点E在AD边上运动的过程中,∠ CB的度数是否存在最大值,若存在,求出此时线段AE的长;若不存在,请说明理由.25. 在△ABC中,AB=2 , CD⊥AB于点D,CD=.
(1)、如图1,求证:∠DE =2∠ABE;(2)、如图2,若点 恰好落在BD上,求tan∠ABE的值;(3)、若AE=2,求 .(4)、点E在AD边上运动的过程中,∠ CB的度数是否存在最大值,若存在,求出此时线段AE的长;若不存在,请说明理由.25. 在△ABC中,AB=2 , CD⊥AB于点D,CD=. (1)、如图1,当点D是线段AB中点时,
(1)、如图1,当点D是线段AB中点时,①AC的长为 ;
②延长AC至点E,使得CE=AC,此时CE与CB的数量关系为 , ∠BCE与∠A的数量关系为 .
(2)、如图2,当点D不是线段AB的中点时,画∠BCE(点E与点D在直线BC的异侧),使∠BCE=2∠A,CE=CB,连接AE.①按要求补全图形;
②求AE的长.
26.(1)、 [问题提出]如图1,已知线段AB=4,点C是一个动点,且点C到点B的距离为2,则线段AC长度的最大值是; (2)、 [问题探究]
(2)、 [问题探究]如图2,以正方形ABCD的边CD为直径作半圆O,E为半圆O上一动点,若正方形的边长为2,求AE长度的最大值;
 (3)、 [问题解决]
(3)、 [问题解决]如图3,某植物园有一块三角形花地ABC,经测量,AC=20米,BC=120米,∠ACB=30°,BC下方有一块空地(空地足够大),为了增加绿化面积,管理员计划在BC下方找一点P,将该花地扩建为四边形ABPC,扩建后沿AP修一条小路,以便游客观赏.考虑植物园的整体布局,扩建部分BPC需满足∠BPC=60°.为容纳更多游客,要求小路AP的长度尽可能长,问修建的观赏小路AP的长度是否存在最大值?若存在,求出AP的最大长度;若不存在,请说明理由.
