广西壮族自治区北海市2022年初中学业水平第一次模拟数学试卷

试卷更新日期：2022-04-29 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列实数中，负数是（）

A、 $\sqrt{2}$ B、－3 C、0.101001 D、 $\frac{1}{3}$

查看试题解析
2. 如图是某几何体的三视图，则该几何体是（）

A、圆柱 B、球 C、正方体 D、长方体

查看试题解析
3. “成语”是中华文化的瑰宝，是中华文化的微缩景观.下列成语：①“水中捞月”，②“守株待兔”，③“百步穿杨”，④“瓮中捉鳖”描述的事件是不可能事件的是（）

A、① B、② C、③ D、④

查看试题解析
4. 华为Mate40 5G手机采用的是麒麟9000芯片，它在指甲盖大小的尺寸上集成了15300000000个晶体管，将15300000000用科学记数法表示为（）

A、 $1.53 \times 1 0^{9}$ B、 $15.3 \times 1 0^{9}$ C、 $1.53 \times 1 0^{10}$ D、 $1.53 \times 1 0^{11}$

查看试题解析
5. 下列计算正确的是（）

A、 $a^{4} \div a = a^{3}$ B、5a－a＝5 C、 $x^{3} + x^{3} = x^{6}$ D、 ${(a b)}^{3} = a^{3} b$

查看试题解析
6. 在2021年初中毕业生体育测试中，某校随机抽取了10名男生的引体向上成绩，将这组数据整理后制成如下统计表：
成绩（次）
12
11
10
9
人数（名）
1
3
4
2
关于这组数据的结论不正确的是（）

A、中位数是10.5 B、平均数是10.3 C、众数是10 D、方差是0.81

查看试题解析
7. 菱形的两条对角线长分别是6和8，则这个菱形的周长是（）

A、24 B、14 C、32 D、20

查看试题解析
8. 如图，⊙O的直径AB垂直于弦CD，垂足为E，∠A=30°，半径为2，则弦CD的长为（）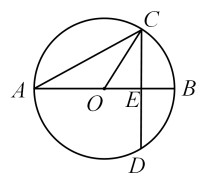

A、2 B、-1 C、 $2 \sqrt{3}$ D、4

查看试题解析
9. 如图，明明家（图中点O处）门前有一条东西走向的公路，经测得有一水塔（图中点A处）在距她家北偏东60°方向的500米处，那么水塔所在的位置到这条公路的距离是（）

A、 $250 \sqrt{3}$ 米 B、250米 C、 $\frac{500 \sqrt{3}}{3}$ 米 D、 $500 \sqrt{2}$ 米

查看试题解析
10. 如图所示，AB是⊙O的直径，PA切⊙O于点A，线段PO交⊙O于点C，连接BC，若 $∠ P = 36 °$ ，则 $∠ B$ 等于（）

A、 $32 °$ B、 $27 °$ C、 $54 °$ D、 $36 °$

查看试题解析
11. 我国古代数学名著《张邱建算经》中记载：“今有清洒一斗直粟十斗，醑酒一斗直粟三斗.今持粟三斛，得酒五斗，问清、醑酒各几何？”意思是：现在一斗清酒价值10斗谷子，一斗醑酒价值3斗谷子，现在拿30斗谷子，共换了5斗酒，问清酒、醑酒各几斗？如果设清酒x斗，醑酒y斗，那么可列方程组为（）

A、 ${\begin{array}{l} x + y = 5 \\ 10 x + 3 y = 30 \end{array}$ B、 ${\begin{array}{l} x + y = 5 \\ 3 x + 10 y = 30 \end{array}$ C、 ${\begin{array}{l} x + y = 30 \\ \frac{x}{10} + \frac{y}{3} = 5 \end{array}$ D、 ${\begin{array}{l} x + y = 30 \\ \frac{x}{3} + \frac{y}{10} = 5 \end{array}$

查看试题解析
12. 如图，在矩形 $A B C D$ 中， $A B = 5$ ， $B C = 5 \sqrt{3}$ ，点P在线段 $B C$ 上运动（含B、C两点），连接 $A P$ ，以点A为中心，将线段 $A P$ 逆时针旋转60°到 $A Q$ ，连接 $D Q$ ，则线段 $D Q$ 的最小值为（）

A、 $\frac{5}{2}$ B、 $5 \sqrt{2}$ C、 $\frac{5 \sqrt{3}}{3}$ D、3

查看试题解析

二、填空题

13. 正六边形每个内角的度数为度.

查看试题解析
14. 因式分解： $x^{2} - 4 =$ .

查看试题解析
15. 3月12日是中国植树节，某学校租了三辆车送同学们去参加“携手共植同心树，植树护绿添新绿”的植树活动，如果小玉和小华每人随机选择搭乘一辆车，则她们恰好选到搭乘同一辆车的概率为.

查看试题解析
16. 如图，AB $∥$ CD，∠AEC＝40°，CB平分∠DCE，则∠ABC的度数为.

查看试题解析
17. 如图，折叠矩形ABCD的一边AD，使点D落在BC边的点F处，已知BF＝6cm，且tan∠BAF＝ $\frac{3}{4}$ ，则折痕AE长是.

查看试题解析
18. 如图，已知直线 $y = k_{1} x$ 与双曲线 $y = \frac{k_{1}}{x}$ 交于A，B两点，将线段AB绕点A沿顺时针方向旋转60°后，点B落在点C处，双曲线 $y = \frac{k_{2}}{x}$ 经过点C，则 $\frac{k_{1}}{k_{2}}$ 的值是.

查看试题解析

三、解答题

19. 计算： ${(- 2)}^{2} + \sqrt{8} \cdot s i n 45 ° - | - 8 |$ .

查看试题解析
20. 解不等式组： ${\begin{array}{l} 2 x - 3 \leq - x ， \\ 1 - \frac{x}{3} > x ， \end{array}$ 并把它的解集在数轴上表示出来.

查看试题解析
21. 如图，在平行四边形ABCD中，AC是它的一条对角线， $B E ⊥ A C$ 于点E.

(1)、过点D作 $D F ⊥ A C$ ，垂足为F；（尺规作图，保留作图痕迹，不写作法）

(2)、求证： $△ A B E ≌ △ C D F$ .

查看试题解析
22. 为宣传6月6日世界海洋日，某校九年级举行了主题为“珍惜海洋资源，保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩的情况，随机抽取了部分参赛学生的成绩，整理并绘制出如下不完整的统计表和统计图（如图）.请根据图表信息解答以下问题：
知识竞赛成绩分组统计表
组别
分数/分
频数
A
60≤x＜70
a
B
70≤x＜80
10
C
80≤x＜90
14
D
90≤x≤100
18

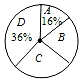(1)、本次调查一共随机抽取了　                  　名参赛学生的成绩；

(2)、表1中a＝　                  　；

(3)、所抽取的参赛学生的成绩的中位数落在的“组别”是　                  　；

(4)、请你估计，该校九年级竞赛成绩达到80分以上（含80分）的学生约有　                  　人.

查看试题解析
23. 如图，在△ABC中，AB=AC，D是BC边上的中点，连结AD，BE平分∠ABC交AC于点E.

(1)、若∠C=36°，求∠BAD的度数；

(2)、过点E作EF $∥$ BC交AB于点F，求证：FB=FE.

查看试题解析
24. 某市计划对道路进行维护．已知甲工程队每天维护道路的长度比乙工程队每天维护道路的长度多50%，甲工程队单独维护30千米道路的时间比乙工程队单独维护24千米道路的时间少用1天．

(1)、求甲、乙两工程队每天维护道路的长度是多少千米？

(2)、若某市计划对200千米的道路进行维护，每天需付给甲工程队的费用为25万元，每天需付给乙工程队的费用为15万元，考虑到要不超过26天完成整个工程，因工程的需要，两队均需参与，该市安排乙工程队先单独完成一部分，剩下的部分两个工程队再合作完成．问乙工程队先单独做多少天，该市需付的整个工程费用最低？整个工程费用最低是多少万元？

查看试题解析
25. 如图，在Rt△ABC中，∠ACB＝90°，AB＝10，AC＝6，点D为BC边上的一个动点，以CD为直径的⊙O交AD于点E，过点C作CF∥AB，交⊙O于点F，连接CE、EF.

(1)、当∠CFE＝45°时，求CD的长；

(2)、求证：∠BAC＝∠CEF；

(3)、是否存在点D，使得 $△$ CFE是以CF为底的等腰三角形，若存在，求出此时CD的长；若不存在，试说明理由.

查看试题解析
26. 如图，在平面直角坐标系xOy中，抛物线y＝﹣ $\frac{1}{2}$ x²+bx+c与x轴正半轴交于点A（4，0），与y轴交于点B（0，2），点C在该抛物线上且在第一象限.

(1)、求该抛物线的表达式；

(2)、将该抛物线向下平移m个单位，使得点C落在线段AB上的点D处，当AD＝3BD时，求m的值；

(3)、联结BC，当∠CBA＝2∠BAO时，求点C的坐标.

查看试题解析

组别	分数/分	频数
A	60≤x＜70	a
B	70≤x＜80	10
C	80≤x＜90	14
D	90≤x≤100	18

成绩（次）	12	11	10	9
人数（名）	1	3	4	2