河南省长垣市2022年九年级中考第一次模拟考试数学试卷
试卷更新日期:2022-04-29 类型:中考模拟
一、单选题
-
1. 下列各数中比 小的数是( )A、 B、 C、 D、2. 天问一号是我国首个软着陆火星的探测器,它承载着中国人对火星探索的期望.截至2021年8月19日晚23时20分,天问一号火星探测器距离地球约8230000公里,8230000用科学记数法表示为( )A、 B、 C、 D、3. 下面的几何图形是由四个相同的小正方体搭成的,其中主视图和左视图相同的是( )A、
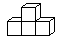 B、
B、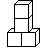 C、
C、 D、
D、 4. 下列运算正确的是( )A、(﹣a)2=﹣a2 B、2a2﹣a2=2 C、a2•a=a3 D、(a﹣1)2=a2﹣15. 如图, , , , 则的度数是( )
4. 下列运算正确的是( )A、(﹣a)2=﹣a2 B、2a2﹣a2=2 C、a2•a=a3 D、(a﹣1)2=a2﹣15. 如图, , , , 则的度数是( )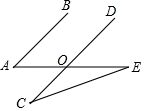 A、10° B、15° C、20° D、25°6. 某校七年级开展“阳光体育”活动,对喜欢乒乓球、足球、篮球、羽毛球的学生人数进行统计(每人只能选择其中一项),得到如图所示的扇形统计图.若喜欢羽毛球的人数是喜欢足球的人数的4倍,喜欢乒乓球的人数是21人,则下列说法不正确的是( )
A、10° B、15° C、20° D、25°6. 某校七年级开展“阳光体育”活动,对喜欢乒乓球、足球、篮球、羽毛球的学生人数进行统计(每人只能选择其中一项),得到如图所示的扇形统计图.若喜欢羽毛球的人数是喜欢足球的人数的4倍,喜欢乒乓球的人数是21人,则下列说法不正确的是( ) A、被调查的学生人数为70人 B、喜欢篮球的人数为14人 C、喜欢足球的扇形的圆心角为36° D、喜欢羽毛球的人数占被调查人数的45%7. 不等式组的解集在数轴上表示为( )A、
A、被调查的学生人数为70人 B、喜欢篮球的人数为14人 C、喜欢足球的扇形的圆心角为36° D、喜欢羽毛球的人数占被调查人数的45%7. 不等式组的解集在数轴上表示为( )A、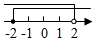 B、
B、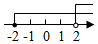 C、
C、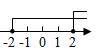 D、
D、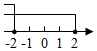 8. 将4个数A,B,C,D排成2行、2列,两边各加一条竖直线记成 , 定义=ad﹣bc.则方程=﹣8的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、只有一个实数根9. 如图,在菱形ABCD中,∠BAD=60°,AB= , 点A,C在直线y=x上,且点A的坐标为( , ).将菱形ABCD绕原点O逆时针旋转,每次旋转45°,则第85次旋转结束时,点C的坐标为( )
8. 将4个数A,B,C,D排成2行、2列,两边各加一条竖直线记成 , 定义=ad﹣bc.则方程=﹣8的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、只有一个实数根9. 如图,在菱形ABCD中,∠BAD=60°,AB= , 点A,C在直线y=x上,且点A的坐标为( , ).将菱形ABCD绕原点O逆时针旋转,每次旋转45°,则第85次旋转结束时,点C的坐标为( ) A、( , 0) B、(0,2) C、(0,) D、(2,0)10. 如图①,在Rt△ABC中,∠ACB=90°,∠A=30°,动点D从点A出发,沿A→C→B以1cm/s的速度匀速运动到点B,过点D作DE⊥AB于点E,图②是点D运动时,△ADE的面积y(cm2)随时间x(s)变化的关系图象,则AB的长为( )
A、( , 0) B、(0,2) C、(0,) D、(2,0)10. 如图①,在Rt△ABC中,∠ACB=90°,∠A=30°,动点D从点A出发,沿A→C→B以1cm/s的速度匀速运动到点B,过点D作DE⊥AB于点E,图②是点D运动时,△ADE的面积y(cm2)随时间x(s)变化的关系图象,则AB的长为( ) A、4cm B、6cm C、8cm D、10cm
A、4cm B、6cm C、8cm D、10cm二、填空题
-
11. 若分式 有意义,则 的取值范围是.12. 请你写出一个经过点(2,1)的函数解析式.13. 为了深化落实“双减”工作,促进中小学生健康成长,教育部门加大了实地督查的力度,对我校学生的作业、睡眠、手机、读物、体质“五项管理”要求的落实情况进行抽样调查,计划从“五项管理”中随机抽取两项进行问卷调查,则抽到“作业”和“手机”的概率为.14. 如图,已知点C、D是以AB为直径的半圆的三等分点,的长为 , 连接OC、AD,则图中阴影部分的面积为.
 15. 如图,在矩形ABCD中,AB=4,BC=6,E是BC的中点,连接AE,P是边AD上一动点,沿过点P的直线将矩形折叠,使点D落在AE上的点D′处,当△APD′是直角三角形时,PD=.
15. 如图,在矩形ABCD中,AB=4,BC=6,E是BC的中点,连接AE,P是边AD上一动点,沿过点P的直线将矩形折叠,使点D落在AE上的点D′处,当△APD′是直角三角形时,PD=.
三、解答题
-
16. 计算及化简:(1)、(2)、17. 为讴歌中华民族实现伟大复兴的奋斗历程,继承革命先烈的优良传统,某中学开展了建党知识测试,该校七、八年级各有300名学生参加,从中各随机抽取了50名学生的成绩(百分制),并对数据(成绩)进行整理,描述和分析,下面给出了部分信息:
a.八年级的频数分布直方图如下(数据分为5组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100);

b.八年级学生成绩在80≤x<90的这一组是:
80 、81、 82 、83、 84、 84、84、84、84、85、85、 86、86.5、87、88、89.5
c.七、八年级学生成绩的平均数、中位数、众数如下:
年级
平均数
中位数
众数
七年级
87.2
85
91
八年级
85.3
m
90
根据以上信息,回答下列问题:
(1)、表中m的值为;(2)、在随机抽样的学生中,建党知识成绩为84分的学生,在年级排名更靠前,理由是;(3)、若各年级建党知识测试成绩前90名将参加线上建党知识竞赛,预估八年级分数至少达到分的学生才能入选;(4)、若成绩85分及以上为“优秀”,请估计八年级达到“优秀”的人数.18. 如图,在平面直角坐标系中,直线与反比例函数(x>0)的图象交于点A,将直线沿y轴向上平移k个单位长度,交y轴于点B,交反比例函数图象于点C,且.AD⊥y轴于点D、CE⊥y于点E. (1)、求证:△BCE∽△OAD;(2)、求点A和点C的坐标;(3)、求k值.19. 如图,CB是⊙O的直径,CF是⊙O的切线,切点为C,点D为直径CB右侧⊙O上一点,连接BD并延长BD,交直线CF于点A,连接OD.
(1)、求证:△BCE∽△OAD;(2)、求点A和点C的坐标;(3)、求k值.19. 如图,CB是⊙O的直径,CF是⊙O的切线,切点为C,点D为直径CB右侧⊙O上一点,连接BD并延长BD,交直线CF于点A,连接OD.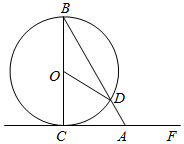 (1)、尺规作图:作出∠COD的角平分线,交CA于点E,连接DE(保留作图痕迹,不写作法);(2)、在(1)的条件下
(1)、尺规作图:作出∠COD的角平分线,交CA于点E,连接DE(保留作图痕迹,不写作法);(2)、在(1)的条件下①求证:DE=AE;
②若⊙O半径为1,当AD的长为 ▲ 时,四边形OCED是正方形.
20. 如图,为了测量山坡上竖直旗杆CD的高度,小明在点A处利用测角仪测得旗杆顶端D的仰角为37°,然后他沿着正对旗杆CD的方向前进10m到达B点处,此时测得旗杆顶部D和底端C的仰角分别为45°和30°,求旗杆CD的高度.(结果精确到0.1m.参考数据: , , , )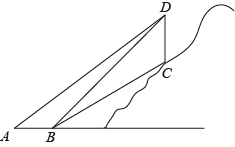 21. 书法是中华民族的文化瑰宝,是人类文明的宝贵财富,是我国基础教育的重要内容.某学校准备为学生的书法课购买一批毛笔和宣纸,已知购买40支毛笔和100张宣纸需要280元;购买30支毛笔和200张宣纸需要260元.(1)、求毛笔和宣纸的单价;(2)、某超市给出以下两种优惠方案:
21. 书法是中华民族的文化瑰宝,是人类文明的宝贵财富,是我国基础教育的重要内容.某学校准备为学生的书法课购买一批毛笔和宣纸,已知购买40支毛笔和100张宣纸需要280元;购买30支毛笔和200张宣纸需要260元.(1)、求毛笔和宣纸的单价;(2)、某超市给出以下两种优惠方案:方案 :购买一支毛笔,赠送一张宣纸;
方案 :购买200张宣纸以上,超出的部分按原价打八折,毛笔不打折.学校准备购买毛笔50支,宣纸若干张(超过200张),选择哪种方案更划算?请说明理由.
22. 如图,直线与x轴交于点A,与y轴交于点B,抛物线经过点A和点B. (1)、求抛物线的解析式;(2)、结合图象直接写出不等式的解集;(3)、若点 , 都在抛物线上,当时,求m的取值范围.23. 在△ABC中,AB=AC,点D为AB边上一动点,∠CDE=∠BAC= , CD=ED,连接BE,EC.
(1)、求抛物线的解析式;(2)、结合图象直接写出不等式的解集;(3)、若点 , 都在抛物线上,当时,求m的取值范围.23. 在△ABC中,AB=AC,点D为AB边上一动点,∠CDE=∠BAC= , CD=ED,连接BE,EC. (1)、问题发现:
(1)、问题发现:如图①,若=60°,则∠EBA= , AD与EB的数量关系是;
(2)、类比探究:如图②,当=90°时,请写出∠EBA的度数及AD与EB的数量关系并说明理由;
(3)、拓展应用:如图③,点E为正方形ABCD的边AB上的三等分点,以DE为边在DE上方作正方形DEFG,点O为正方形DEFG的中心,若OA= , 请直接写出线段EF的长度