河南省信阳市2022年中考数学一模试卷
试卷更新日期:2022-04-29 类型:中考模拟
一、单选题
-
1. 下列各数: , , 0, , 其中比小的数是( )A、 B、 C、0 D、2. 如图,将一个圆柱体放置在长方体上,其中圆柱体的底面直径与长方体的宽相平,则该几何体的左视图是( )
 A、
A、 B、
B、  C、
C、 D、
D、 3. 我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作,根据规划“一带一路”地区覆盖总人口为人,的原数是( )A、440000000 B、44000000000 C、440000000000 D、44000000004. 下列运算一定正确的是( )A、a2+a2=a4 B、a2•a4=a8 C、(a2)4=a8 D、(a+b)2=a2+b25. 如图,已知直线AD、BE、CF相交于点O,OG⊥AD,且∠BOC=35°,∠FOG=30°,则∠DOE的度数为( )
3. 我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作,根据规划“一带一路”地区覆盖总人口为人,的原数是( )A、440000000 B、44000000000 C、440000000000 D、44000000004. 下列运算一定正确的是( )A、a2+a2=a4 B、a2•a4=a8 C、(a2)4=a8 D、(a+b)2=a2+b25. 如图,已知直线AD、BE、CF相交于点O,OG⊥AD,且∠BOC=35°,∠FOG=30°,则∠DOE的度数为( ) A、 B、 C、 D、6. 下列关于 的一元二次方程中,有两个不相等的实数根的方程是( )A、 B、 C、 D、7. 在4张完全相同的卡片上分别标上2,3,4,5这四个数字,任意抽取两张卡片并将所标数字组成一个两位数,则这个两位数能被3整除的概率是( )A、 B、 C、 D、8. 如图,点A在双曲线y═ (x>0)上,过点A作AB⊥x轴,垂足为点B,分别以点O和点A为圆心,大于 OA的长为半径作弧,两弧相交于D,E两点,作直线DE交x轴于点C,交y轴于点F(0,2),连接AC.若AC=1,则k的值为( )
A、 B、 C、 D、6. 下列关于 的一元二次方程中,有两个不相等的实数根的方程是( )A、 B、 C、 D、7. 在4张完全相同的卡片上分别标上2,3,4,5这四个数字,任意抽取两张卡片并将所标数字组成一个两位数,则这个两位数能被3整除的概率是( )A、 B、 C、 D、8. 如图,点A在双曲线y═ (x>0)上,过点A作AB⊥x轴,垂足为点B,分别以点O和点A为圆心,大于 OA的长为半径作弧,两弧相交于D,E两点,作直线DE交x轴于点C,交y轴于点F(0,2),连接AC.若AC=1,则k的值为( ) A、2 B、 C、 D、9. 如图,平面直角坐标系中,A(4,0),点B为y轴上一点,连接AB,tan∠BAO=2,点C,D为OB,AB的中点,点E为射线CD上一个动点、当△AEB为直角三角形时,点E的坐标为( )
A、2 B、 C、 D、9. 如图,平面直角坐标系中,A(4,0),点B为y轴上一点,连接AB,tan∠BAO=2,点C,D为OB,AB的中点,点E为射线CD上一个动点、当△AEB为直角三角形时,点E的坐标为( ) A、(4,4)或(22,4) B、(4,4)或(22,4) C、(12,4)或(22,4) D、(12,4)或(22,4)10. 如图1,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD , 图中阴影为重合部分,则阴影部分的面积为( )
A、(4,4)或(22,4) B、(4,4)或(22,4) C、(12,4)或(22,4) D、(12,4)或(22,4)10. 如图1,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD , 图中阴影为重合部分,则阴影部分的面积为( )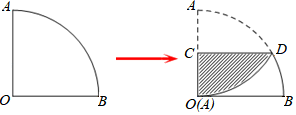 A、6π﹣ B、6π﹣9 C、12π﹣ D、
A、6π﹣ B、6π﹣9 C、12π﹣ D、二、填空题
-
11. 比较大小:25.(选填“>”“<”或“=”)12. 如图,直线AB与直线CD相交于点O,点E是∠COB内一点,且OE⊥AB,∠AOC=35°,则∠EOD的度数是.
 13. 如图所示的网格中,每个小正方形的边长为1,点A,B,C均为小正方形的顶点,且点B在上,则阴影部分的面积为.
13. 如图所示的网格中,每个小正方形的边长为1,点A,B,C均为小正方形的顶点,且点B在上,则阴影部分的面积为. 14. 如图1,在平面直角坐标系中,直线yx+m(m>0)与直线y=2x交于点4,与x轴交于点B,点O为坐标原点,点C在线段OB上,且不与点B重合,过点C作垂直于x轴的直线,交直线AB于点D,将△BCD沿CD翻折,得到△ECD.设点C的坐标为(x,0),△CDE与△AOB重叠部分的面积为S,S关于x的函数图象如图2所示,则m=.
14. 如图1,在平面直角坐标系中,直线yx+m(m>0)与直线y=2x交于点4,与x轴交于点B,点O为坐标原点,点C在线段OB上,且不与点B重合,过点C作垂直于x轴的直线,交直线AB于点D,将△BCD沿CD翻折,得到△ECD.设点C的坐标为(x,0),△CDE与△AOB重叠部分的面积为S,S关于x的函数图象如图2所示,则m=.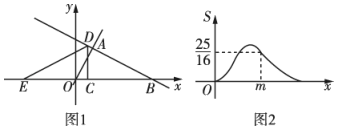 15.
15.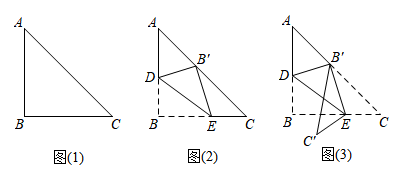
如图(1),在等腰直角三角形纸片ABC中,∠B=90°,AB=22,点D,E分别为AB,BC上的动点.将纸片沿DE翻折,点B的对应点B'恰好落在边AC上,如图(2),再将纸片沿B'E翻折,点C的对应点为C',如图(3).当△DB'E,△B'C'E的重合部分(即阴影部分)为直角三角形时,CE的长为.
三、解答题
-
16.(1)、计算:|﹣4|﹣()﹣2tan30°+.(2)、化简:.17. 地铁为我们提供了方便、舒适、快捷的出行条件,但地铁上也有一些不文明的现象.某市记者为了解“乘坐地铁时的不文明行为”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.
组别
观点
频数(人数)
A
破坏先下后上的规矩堵进出口
80
B
占座
m
C
拒绝安检
n
D
吃东西、随手丢垃圾
120
E
其他
60

请根据图表中提供的信息解答下列问题.
(1)、填空:m= , n= , 扇形统计图中E组所占的百分比为%.(2)、若从这次接受调查的市民中随机抽出一人,则此人持C组观点的概率是多少?(3)、若该市约有100万人,请你估计其中持D组观点的人数.18. 如图,在△ABC中,AB=AC=6cm,∠BAC=45°,以AB为直径作⊙O,分别与AC,BC相交于点E,D,连接DE,BE,点F从点A出发,在直径AB的上方沿以1cm/s的速度向点B运动,连接AF,BF.设点F运动的时间为t(s). (1)、求证:△ABC∽△DEC;(2)、填空:①当t= s时,四边形AEBF为正方形.
(1)、求证:△ABC∽△DEC;(2)、填空:①当t= s时,四边形AEBF为正方形.②当t= s时,S△ABFS△ABE.
19. 如图,在矩形OABC中,BC=4,OC,OA分别在x轴、y轴上,对角线OB,AC交于点E;过点E作EF⊥OB,交x轴于点F.反比例函数(x>0)的图象经过点E,且交BC于点D,已知S△OEF=5,CD=1. (1)、求OF的长;(2)、求反比例函数的解析式;(3)、将△OEF沿射线EB向右上方平移个单位长度,得到△O'E'F',则EF的对应线段E'F'的中点(填“能”或“不能”)落在反比例函数(x>0)的图上.20. 如图(1)为某大型商场的自动扶梯,图(2)中的AB为从一楼到二楼的扶梯的侧面示意图.小明站在扶梯起点A处时,测得天花板上日光灯C的仰角为37°,此时他的眼睛D与地面的距离AD=1.8m,之后他沿一楼扶梯到达顶端B后又沿BL(BL∥MN)向正前方走了2m,发现日光灯C刚好在他的正上方.已知自动扶梯AB的坡度为1:2.4,AB的长度是13m,求日光灯C到一楼地面的高度.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
(1)、求OF的长;(2)、求反比例函数的解析式;(3)、将△OEF沿射线EB向右上方平移个单位长度,得到△O'E'F',则EF的对应线段E'F'的中点(填“能”或“不能”)落在反比例函数(x>0)的图上.20. 如图(1)为某大型商场的自动扶梯,图(2)中的AB为从一楼到二楼的扶梯的侧面示意图.小明站在扶梯起点A处时,测得天花板上日光灯C的仰角为37°,此时他的眼睛D与地面的距离AD=1.8m,之后他沿一楼扶梯到达顶端B后又沿BL(BL∥MN)向正前方走了2m,发现日光灯C刚好在他的正上方.已知自动扶梯AB的坡度为1:2.4,AB的长度是13m,求日光灯C到一楼地面的高度.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75) 21. 为美化校园,某校需补栽甲、乙两种花苗.经咨询,这两种花苗的价格都有零售价和批发价之分(若按批发价购买,则每种花苗购买数量不少于100株),零售时每株甲种花苗比每株乙种花苗多5元.已知用零售价购买相同数量的甲、乙两种花苗,所用费用分别是100元、50元.(1)、求甲、乙两种花苗的零售价;(2)、该校预计批发这两种花苗共1000株,且甲种花苗的数量不少于乙种花苗数量的 , 甲、乙两种花苗的批发价分别为8元/株、2元/株.设甲种花苗的批发数量为m株,相比按零售价购买可节约的资金总额为W元,求W与m之间的函数关系式,并求节约资金总额的最大值.22. 如图,抛物线y=ax2+3x+c与x轴交于点A,B,直线y=x+1与抛物线交于点A,C(3,n).点P为抛物线上一动点,其横坐标为m.
21. 为美化校园,某校需补栽甲、乙两种花苗.经咨询,这两种花苗的价格都有零售价和批发价之分(若按批发价购买,则每种花苗购买数量不少于100株),零售时每株甲种花苗比每株乙种花苗多5元.已知用零售价购买相同数量的甲、乙两种花苗,所用费用分别是100元、50元.(1)、求甲、乙两种花苗的零售价;(2)、该校预计批发这两种花苗共1000株,且甲种花苗的数量不少于乙种花苗数量的 , 甲、乙两种花苗的批发价分别为8元/株、2元/株.设甲种花苗的批发数量为m株,相比按零售价购买可节约的资金总额为W元,求W与m之间的函数关系式,并求节约资金总额的最大值.22. 如图,抛物线y=ax2+3x+c与x轴交于点A,B,直线y=x+1与抛物线交于点A,C(3,n).点P为抛物线上一动点,其横坐标为m. (1)、求抛物线的解析式及其顶点的坐标;(2)、已知直线l:x=m+5与直线AC交于点D,过点P作PE⊥l于点E,以PE,DE为边作矩形PEDF.
(1)、求抛物线的解析式及其顶点的坐标;(2)、已知直线l:x=m+5与直线AC交于点D,过点P作PE⊥l于点E,以PE,DE为边作矩形PEDF.①当抛物线的顶点在矩形PEDF内部时,请直接写出m的取值范围.
②在①的条件下,求矩形PEDF的周长的最小值.
23. 在△ABC中,AB=AC,∠BAC=90°,点D,E分别是AC,BC的中点,点P是直线DE上一点,连接AP,将线段PA绕点P顺时针旋转90°得到线段PM,连接AM,CM. (1)、问题发现
(1)、问题发现如图(1),当点P与点D重合时,线段CM与PE的数量关系是 , ∠ACM=°.
(2)、探究证明当点P在射线ED上运动时(不与点E重合),(1)中结论是否一定成立?请仅就图中的情形给出证明.
(3)、问题解决连接PC,当△PCM是等边三角形时,请直接写出的值.