河南省信阳市2022年中考第一次模拟考试数学试卷

试卷更新日期：2022-04-29 类型：中考模拟

进入出卷网下载

一、单选题

1. $- \frac{1}{3}$ 的绝对值是（）

A、 $3$ B、 $- 3$ C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
2. 信阳是中国毛尖之都，信阳毛尖是中国十大名茶之一，2021年信阳毛尖品牌价值达71.08亿元，连续12年位居全国前三位.数据“71.08亿”用科学记数法表示是（）

A、7.108×10⁹ B、71.08×10⁹ C、7.108×10¹⁰ D、71.08×10¹⁰

查看试题解析
3. 如图是由6个相同的小正方体组成的几何体，其主视图是（）

A、 B、 C、 D、

查看试题解析
4. 下列计算正确的是（）

A、a⁴·a²=a⁸ B、(a²)³=a⁶ C、(3a)²=3a² D、2a⁸÷a²=a⁴

查看试题解析
5. 如图，AB $∥$ CD，EF分别交AB，CD于E，F，EG⊥AB，已知∠FEG=25°，则∠CFE的度数是（）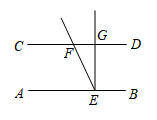

A、125° B、130° C、155° D、115°

查看试题解析
6. 下列关于矩形的说法不正确的是（）

A、对角线平分且相等 B、四个角都是直角 C、有四条对称轴 D、是中心对称图形

查看试题解析
7. 若一元二次方程-x²-bx+c=0中c>0，则方程的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断

查看试题解析
8. 信阳是河南传统餐饮历史文化名城，信阳菜历经千年的积淀和发展，以鲜、香、爽、醇、中的独特味道传遍大江南北.某游客慕名而来，决定从“筒鲜鱼”“固始鹅块”“石凉粉”“罗山大肠汤”“闷罐肉”这5个特色美食中随机选取2 个进行品尝，则他抽到“筒鲜鱼”和“固始鹅块”的概率为（）

A、 $\frac{2}{5}$ B、 $\frac{1}{6}$ C、 $\frac{1}{10}$ D、 $\frac{1}{12}$

查看试题解析
9. 如图，矩形ABCD中，AD=2，AB= $\sqrt{3}$ ，对角线AC上有一点G（异于A，C），连接 DG，将△AGD绕点A 逆时针旋转60°得到△AEF，则BF的长为（）

A、 $\sqrt{13}$ B、2 $\sqrt{13}$ C、 $\sqrt{7}$ D、2 $\sqrt{7}$

查看试题解析
10. 如图1，点Q为菱形ABCD的边BC上一点，将菱形 ABCD沿直线AQ 翻折，点B的对应点P落在BC的延长线上.已知动点M从点B出发，在射线 BC上以每秒1个单位长度运动.设点M运动的时间为x，△APM的面积为y.图2为y关于x的函数图象，则菱形 ABCD的面积为（）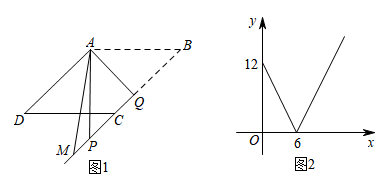

A、12 B、24 C、10 D、20

查看试题解析

二、填空题

11. 当分式 $\frac{x^{2} - 9}{2 x - 6} = 0$ 时，x的值为

查看试题解析
12. 已知直线l：y=（3-k）x+1经过点（4，9），则它的解析式为.

查看试题解析
13. 信阳是全国有名的板栗之乡，板栗年产量达数百万千克.某农场准备从甲、乙、丙三个品种的板栗树中选出一种产量既高又稳定的板栗树进行种植，现随机从这三个品种的板栗树中各选10棵，每棵产量的平均数 $\bar{x}$ （单位：千克）及方差如下表所示.该农场应选的品种
是

甲
乙
丙
$\bar{x}$
43
43
41
$S^{2}$
1.2
1.1
1.2

查看试题解析
14. 如图，点 A、B，C均在圆上，若 AB=1，BC=2，∠ABC=60°，则 $\overset{⌢}{A B}$ 的长为.（结果保留π）

查看试题解析
15. 李明用一张矩形纸片玩折纸游戏.如图1.将矩形纸片ABCD沿过点D的直线折叠，使点A落在CD上的点A'处，得到折痕DE，然后把纸片展平；如图2，将图1中的矩形纸片 ABCD沿过点E的直线折叠，点C恰好落在AD上的点C'处，点B落在点B'处，得到折痕 EF，B'C'交AB于点M，C'F交DE 于点N.已知AB=4，AD=3，则的值为 $\frac{M C^{'}}{C^{'} F}$ 的值为

查看试题解析

三、解答题

16.

(1)、计算： $| \sqrt{25} - 2 | + (\sqrt{5})^{0} - \sqrt[3]{125}$

(2)、化简 $\frac{x^{2} - 2 x}{x^{2} - 4} \div (1 - \frac{1}{x + 2})$

查看试题解析
17. 国家实施“双减”政策后，学生学业负担有所减轻，很多家长选择利用周末时间带孩子去景区游玩.某调查小组从去过南湾湖和鸡公山的学生中各随机抽取了 20名学生对这两个景区分别进行评分（满分10分），并通过整理和分析，给出了部分信息. 南湾湖景区得分情况：
7，8，7，10，7，6，9，9，10，10，8，9，8，6，6，10，9，7，9，9.
鸡公山景区得分情况扇形统计图
抽取的学生对两个景区分别打分的平均数、众数和中位数如下表.

平均数
众数
中位数
南湾湖
8.2
9
b
鸡公山
7.8
c
8
根据以上信息，解答下列问题：

(1)、求上述图表中的 a，b，c 的值；

(2)、根据上述数据，你认为去过这两个景区的学生对哪个景区评价更高?请说明理由（写出一条理由）.

查看试题解析
18. 如图，直线y=-2x+b与x轴、y轴分别相交于点 A，B，以线段 AB为边在第一象限作正方形ABCD，已知AB=2 $\sqrt{5}$

(1)、求直线 AB的解析式；

(2)、求点D的坐标，并判断点D是否在双曲线y= $\frac{12}{x}$ ，说明理由.

查看试题解析
19. 据《映象网》2022年2月17 日报道，为了增加绿地，还绿于民，提升景观质量，作为承载着很多郑州人记忆的标志性建筑——人民公园摩天轮可能面临拆除.消息传出后，市民纷纷前来打卡，乘坐“最后一次”.摩天轮是一种大型转轮状的机械建筑设施，上面挂在轮边缘的是供乘客乘搭的座舱.乘客坐在摩天轮上，可以从高处俯瞰四周景色.如图是建在山上的一个摩天轮的示意图，小华在 A处测得摩天轮顶端D的仰角为54°，然后乘坐缆车到达B处，已知 AE//BF，AB的坡度i=3：4，且 AB=40m，BC=50 m，CD⊥BF于点C.求摩天轮的高度 CD.（精确到0.1 m，参考数据：sin 54°≈0.81，cos 54°≈0.59，tan 54°≈1.38）

查看试题解析
20. 如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，交AC于点E，过点D作DF⊥AC于点F，交 AB 的延长线于点G.

(1)、求证：DF 是⊙O的切线；

(2)、若CF=1，∠ACB=60°，求图中阴影部分的面积.

查看试题解析
21. 随着 2022年北京冬奥会的进行，冬奥会吉样物“冰墩墩”和冬残奥会吉祥物“雪容融”深受广大人民的喜爱.某网店2021年12月份上架了“冰墩墩”和“雪容融”，当月售出了100个“冰墩墩”和40个“雪容融”，销售总额为14 800元.2022年1月售出了160个“冰墩墩”和60 个“雪容融”，销售总额为23 380元.

(1)、求“冰墩墩”和“雪容融”的销售单价；

(2)、店主2022年2月又购进了200个“冰墩墩”和160个“雪容融”上架到网店，在“冰墩墩”售出 $\frac{3}{4}$ ， “雪容融”售出 $\frac{1}{2}$ 后，为了尽快回笼资金，店主决定对剩余的“冰墩墩”每个打a折销售，对剩余的“雪容融”每个降价3a元销售，很快全部售完.若要保证本月销售总额不低于32500元，求a的最小值.

查看试题解析
22. 如图，抛物线y=-x²+bx+c与x轴交于点A（-1，0）和B（3，0），与y轴交于点C.

(1)、求抛物线的解析式；

(2)、若P为抛物线的顶点，动点Q在y轴右侧的抛物线上，是否存在点Q使∠QCO=∠PBC?若存在，请求出点Q的坐标.若不存在，请说明理由.

查看试题解析
23. 在直线m上依次取互不重合的三个点D，A，E，在直线m上方有AB=AC，且满足∠BDA＝∠AEC＝∠BAC＝α.

(1)、如图1，当α=90°时，猜想线段DE，BD，CE之间的数量关系是；

(2)、如图2，当0°＜α＜180°时，问题（1）中结论是否仍然成立？如成立，请你给出证明；若不成立，请说明理由；

(3)、拓展与应用：如图3，当α=120°时，点F为∠BAC平分线上的一点，且AB=AF，分别连接FB，FD，FE，FC，试判断△DEF的形状，并说明理由.

查看试题解析

	甲	乙	丙
$\bar{x}$	43	43	41
$S^{2}$	1.2	1.1	1.2

	平均数	众数	中位数
南湾湖	8.2	9	b
鸡公山	7.8	c	8