河南省新乡市辉县2022年九年级下学期中考数学第一次数学模拟试卷

试卷更新日期：2022-04-29 类型：中考模拟

进入出卷网下载

一、单选题

1. －3的绝对值是（）

A、1 B、±3 C、3 D、－3

查看试题解析
2. 千磨万击还坚劲，任尔东西南北风.在全球疫情肆虐的大背景下，一场自上世纪大萧条以来最严重的经济衰退也随之而来，但是率先控制疫情、率先启动复工复产、率先实现经济增长转正的中国，1月18日，国家统计局发布了2020年中国经济年报，经过初步核算，全年国内生产总值达101万亿元！数据101万亿用科学记数法可表示为（　　）

A、10.1×10¹⁰ B、1.01×10¹¹ C、1.01×10¹³ D、1.01×10¹⁴

查看试题解析
3. 下列计算结果正确的是（）

A、a⁸÷a⁴=a² B、a²•a³=a⁶ C、（a³）²=a⁶ D、（﹣2a²）³=8a⁶

查看试题解析
4. 现在道路上的车辆是越来越多了，如果没有交通规则约束和交通标志指示，那么路上的车辆一定是混杂堵塞，所以开车时一定要看清标志，文明驾车.下列交通标志中，既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
5. 已知 $\frac{x}{x + y} = \frac{3}{5}$ ，则 $\frac{y}{x}$ ＝（）

A、 $\frac{2}{5}$ B、 $\frac{3}{4}$ C、 $\frac{3}{2}$ D、 $\frac{2}{3}$

查看试题解析
6. 把一副直角三角板按如图所示的方式摆放在一起，其中 $∠ C = 9 0^{∘}$ ， $∠ F = 9 0^{∘}$ ， $∠ D = 3 0^{∘}$ ， $∠ A = 4 5^{∘}$ ，则 $∠ 1 + ∠ 2$ 等于 $($ 　　 $)$

A、 $27 0^{∘}$ B、 $21 0^{∘}$ C、 $18 0^{∘}$ D、 $15 0^{∘}$

查看试题解析
7. 如图，在⊙O中， $\overset{⌢}{A B}$ ＝ $\overset{⌢}{A C}$ ，∠AOB＝40°，则∠ADC的度数是（）

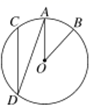A、40° B、30° C、20° D、15°

查看试题解析
8. 如图，菱形ABCD放置在直线l上（AB与直线l重合），AB＝4，∠DAB＝60°，将菱形ABCD沿直线l向右无滑动地在直线l上滚动，从点A离开出发点到点A第一次落在直线l上为止，点A运动经过的路径总长度为（）

A、 $\frac{16 \sqrt{3} π}{3}$ B、 $\frac{16 π}{3}$ C、 $\frac{4 π}{3} + \frac{4 \sqrt{3} π}{3}$ D、 $\frac{8 π}{3} + \frac{8 \sqrt{3} π}{3}$

查看试题解析
9. 对于二次函数y＝ax²﹣2ax﹣3a+3的性质，下列说法中错误的是（）

A、抛物线的对称轴为直线x＝1 B、抛物线一定经过两定点（﹣1，3）与（3，3） C、当a＜0时，抛物线与x轴一定有两个不同的交点 D、当a＞0时，抛物线与x轴一定有两个不同的交点

查看试题解析
10. 如图，已知四边形ABCD为矩形，点B在第一象限角平分线上，OB＝ $\sqrt{2}$ AB，反比例函数y＝ $\frac{k}{x}$ （k＞0）过点A交BC于点E，连接OA、AE、OE，△AOE的面积为6，过点A交BC于点E，连接OA、AE、OE，则k＝（）

A、4 B、6 C、8 D、10

查看试题解析

二、填空题

11. 如图，在平面直角坐标系中，函数y＝kx＋b(k≠0)与y＝ $\frac{m}{x}$ (m≠0)的图象相交于点A(2，3)，B(－6，－1)，则关于x的不等式kx＋b＞ $\frac{m}{x}$ 的解集是.

查看试题解析
12. 已知 $x_{1}$ ， $x_{2}$ 是方程 $x^{2} + 6 x + 3 = 0$ 的两个实数根，则 $\frac{x_{2}}{x_{1}} + \frac{x_{1}}{x_{2}}$ 的值等于．

查看试题解析
13. 如图，四边形ABCD是菱形，O是两条对角线的交点，过O点的三条直线将菱形分成阴影和空白部分．当菱形的两条对角线的长分别为6和8时，则阴影部分的面积为．

查看试题解析
14. 如图，四边形 $A B C D$ 为正方形，且边长 $A B = 15$ ，点 $E$ 是以 $A B$ 为直径的圆上一动点，当 $t a n ∠ E A B = \frac{3}{4}$ 时， $D E$ 的长度为.

查看试题解析
15. 如图，矩形ABCD中，AD=2，AB=5，P为CD边上的动点，当△ADP与△BCP相似时，DP=.

查看试题解析

三、解答题

16. 计算：

(1)、计算： $2^{2} - (- \frac{1}{2})^{- 2} + 3^{- 1} - \sqrt{\frac{1}{9}} + (π - 3.14)^{0}$

(2)、计算： $\frac{a^{2}}{a - 3} - a - 3$

(3)、计算，使结果不含负整指数幂： ${(3 a^{2} b)}^{- 2} {(a^{- 3} b^{- 2})}^{- 1}$

查看试题解析
17. 一个不透明的布袋里装有2个白球，1个黑球和若干个红球，它们除颜色外其余都相同，从中任意摸出1个球，是白球的概率为 $\frac{1}{2}$ 。

(1)、布袋里红球有多少个？

(2)、先从布袋中摸出1个球后不放回，再摸出1个球，请用列表或画树状图等方法求出两次摸到的球都是白球的概率。

查看试题解析
18. 目前节能灯在城市已基本普及，今年全省面向县级及农村地区推广，为响应号召，某商场计划购进甲，乙两种节能灯共1200只，这两种节能灯的进价、售价如下表：

进价（元/只）

售价（元/只）

甲型

25

30

乙型

45

60

(1)、如何进货，进货款恰好为46000元？

(2)、如何进货，商场销售完节能灯时获利最多且不超过进货价的30%，此时最大利润为多少元？

查看试题解析
19. 如图，已知⊙O的直径AB＝4，点C、D分别为⊙O上的两点， $\overset{⌢}{C D} = \overset{⌢}{B D}$ ，过点D作DE⊥AB于点E，⊙O的切线DF与直线AF交于点F，且AF过点C，连接BD、AD.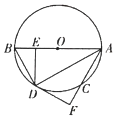

(1)、求证：CF＝BE；

(2)、填空：
①当AD＝时，四边形AODC是菱形；
②当AD＝时，四边形AEDF是正方形.

查看试题解析
20. 学校运动场的四角各有一盏探照灯，其中一盏探照灯B的位置如图所示，已知坡长AC＝12m，坡角α为30°，灯光受灯罩的影响，最远端的光线与地面的夹角β为27°，最近端的光线恰好与地面交于坡面的底端C处，且与地面的夹角为60°，A、B、C、D在同一平面上.（结果精确到0.1m.参考数据：sin27°≈0.45，cos27°≈0.89，tan27°≈0.50， $\sqrt{3} \approx$ 1.73.）

(1)、求灯杆AB的高度；

(2)、求CD的长度.

查看试题解析
21. 如图，已知 $A (- 4 ， \frac{1}{2}) ， B (- 1 ， m)$ 是一次函数 $y = k x + b$ 与反比例函数 $y = - \frac{2}{x} (x < 0)$ 图象的两个交点， $A C ⊥ x$ 轴于 $C ， B D ⊥ y$ 轴于 $D$ .

(1)、求一次函数解析式及 $m$ 的值；

(2)、 $P$ 是线段 $A B$ 上的一点，连接 $P C ， P D ，$ 若 $△ P C A$ 和 $△ P D B$ 面积相等，求点 $P$ 坐标.

查看试题解析
22. 在平面直角坐标系中，已知点 $A (1 ， 4)$ ， $B (- 1 ， 0)$ ， $C (0 ， 2)$ ，抛物线 $y = a x^{2} + b x + 3$ 经过A，B，C三点中的两点.

(1)、求抛物线的表达式；

(2)、点 $M (m ， n)$ 为（1）中所求抛物线上一点，且 $0 < m < 4$ ，求n的取值范围；

(3)、一次函数 $y = (k - 1) x - 3 k + 3$ （其中 $k \neq 1)$ 与（1）中所求抛物线交点的横坐标分别是 $x_{1}$ 和 $x_{2}$ ，且 $x_{1} < - 1 < x_{2}$ ，请直接写出k的取值范围.

查看试题解析
23. 如图1，在 $△ A B C$ 中， $∠ B C A = 90 °$ ， $A C = 3$ ， $B C = 4$ ，点 $P$ 为斜边 $A B$ 上一点，过点 $P$ 作射线 $P D ⊥ P E$ ，分别交 $A C$ 、 $B C$ 于点 $D$ ， $E$ ．

(1)、问题产生
若 $P$ 为 $A B$ 中点，当 $P D ⊥ A C$ ， $P E ⊥ B C$ 时， $\frac{P D}{P E} =$ ；

(2)、问题延伸
在（1）的情况下，将若 $∠ D P E$ 绕着点 $P$ 旋转到图2的位置， $\frac{P D}{P E}$ 的值是否会发生改变？如果不变，请证明；如果改变，请说明理由；

(3)、问题解决
如图3，连接 $D E$ ，若 $△ P D E$ 与 $△ A B C$ 相似，求 $B P$ 的值．

查看试题解析

	进价（元/只）	售价（元/只）
甲型	25	30
乙型	45	60