河南省商丘市永城四中2022年普通高中招生考试模拟试卷数学试卷

试卷更新日期：2022-04-29 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，小于 $- 3$ 的数是（）

A、 $1$ B、 $0$ C、 $- 4$ D、 $- 2$

查看试题解析
2. 某正方体的每个面上都有一个汉字，如图是它的一种展开图，那么在原正方体中，与“祝”字所在面相对的面上的汉字是（）

A、考 B、试 C、顺 D、利

查看试题解析
3. 如图，将一块三角尺的直角顶点放在直尺的一边上，当∠1=35°时，∠2的度数为（）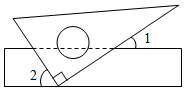

A、35° B、45° C、55° D、65°

查看试题解析
4. 下列运算正确的是（）

A、 $2 a + 3 a = 5 a^{2}$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、 $(- a b^{2})^{3} = - a^{3} b^{6}$ D、 $(a + 2 b)^{2} = a^{2} + 4 b^{2}$

查看试题解析
5. 生物工作者为了估计一片山林中雀鸟的数量，设计了如下方案：先捕捉100只雀鸟，给它们做上标记后放回山林；一段时间后，再从中随机捕捉500只，其中有标记的雀鸟有5只．请你帮助工作人员估计这片山林中雀鸟的数量约为（　　）

A、1000只 B、10000只 C、5000只 D、50000只

查看试题解析
6. 一元二次方程 $x (x - 2) = x - 2$ 的解是（）

A、 $x_{1} = x_{2} = 0$ B、 $x_{1} = x_{2} = 1$ C、 $x_{1} = 1$ ， $x_{2} = 2$ D、 $x_{1} = 0$ ， $x_{2} = 2$

查看试题解析
7. 如图， $▱$ $A B C D$ 的对角线AC，BD相交于点O， $E$ 是AB中点，且AE+EO=4，则 $▱ A B C D$ 的周长为（）

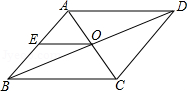A、20 B、16 C、12 D、8

查看试题解析
8. 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题：“一条竿子一条索，索比竿子长一托.折回索子却量竿，却比竿子短一托.”其大意为：现有一根竿和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短5尺.设绳索长x尺.则符合题意的方程是（）

A、 $\frac{1}{2} x = (x - 5) - 5$ B、 $\frac{1}{2} x = (x + 5) + 5$ C、 $2 x = (x - 5) - 5$ D、 $2 x = (x + 5) + 5$

查看试题解析
9. 抛物线 $y = a x^{2} + b x + c$ 的部分图象如图所示，若点 $A (- 2 ， y_{1})$ ， $B (2 ， y_{2})$ ， $C (4 ， y_{3})$ 在抛物线上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{1} = y_{2} < y_{3}$ B、 $y_{1} = y_{2} > y_{3}$ C、 $y_{1} = y_{3} < y_{2}$ D、 $y_{1} = y_{3} > y_{2}$

查看试题解析
10. 如图，等边 $△ A B C$ 的顶点 $A (1 ， 1)$ ， $B (3 ， 1)$ ，规定把 $△ A B C$ “先沿 $x$ 轴翻折，再向右平移1个单位”为一次变换，这样连续经过2022次变换后，等边 $△ A B C$ 的顶点 $C$ 的坐标为（）

A、 $(2023 ， \sqrt{3} + 1)$ B、 $(2023 ， - \sqrt{3} - 1)$ C、 $(2024 ， \sqrt{3} + 1)$ D、 $(2024 ， - \sqrt{3} - 1)$

查看试题解析

二、填空题

11. 在物联网时代的所有芯片中，14nm芯片已成为需求的焦点.已知nm即纳米，是长度的度量单位， $1 n m = 1 \times 1 0^{- 9} m$ .将14nm用科学记数法表示为m.

查看试题解析
12. 分解因式： $x^{2} - 4 y^{2} =$ .

查看试题解析
13. 北京冬奥会的竞赛场馆建设各具特色，其中国家速滑馆“冰丝带”、国家雪车雪橇中心“雪游龙”、国家跳台滑雪中心“雪如意”等新建场馆，充分融入了中国文化元素，已成为令人瞩目的标志性建筑.小华和小丽参加了冬奥志愿者服务，并被随机分配到以上三个场馆中，则她们恰好被分到同一个场馆的概率为.

查看试题解析
14. 如图1，点P从 $△ A B C$ 的顶点A出发，以每秒2个单位长度的速度沿 $A \to B \to C \to A$ 的方向匀速运动到点A.图2是点P运动时线段 $A P$ 的长度y随时间t（s）变化的关系图象，其中点M为曲线部分的最低点，则 $△ A B C$ 的面积是.

查看试题解析
15. 如图，将边长为3的菱形 $A B C D$ 绕点A逆时针旋转到菱形 $A B^{^{'}} C^{^{'}} D^{^{'}}$ 的位置，使点 $B^{'}$ 落在 $B C$ 上， $B^{^{'}} C^{^{'}}$ 与 $C D$ 交于点E.若 $B B^{^{'}} = 1$ ，则 $C E$ 的长为.

查看试题解析

三、解答题

16.

(1)、计算： $\sqrt{12} + | \sqrt{3} - 3 | - {(\frac{1}{3})}^{- 1}$ ；

(2)、解方程： $\frac{2}{x - 2} - 1 = \frac{3}{2 - x}$

查看试题解析

17. 近年来网约车给人们的出行带来了便利．初三的王冬和数学兴趣小组的同学对“美团”和“滴滴”两家网约车公司司机月收入进行了一项抽样调查，两家公司分别抽取的10名司机月收入（单位：千元）如图所示：

根据以上信息，整理分析数据如下：

	平均月收入	中位数	众数	方差
“美团”	a	6	c	1.2
“滴滴”	6	b	4	7.6

(1)、填空：

a =

；

b =

；

c =

；

(2)、王冬的叔叔决定从两家公司中选择一家做网约车司机，如果你是王冬，你建议他选哪家公司？说明理由.

查看试题解析

18. 已知正比例函数 $y = k x (k \neq 0)$ 与反比例函数 $y = \frac{6}{x}$ 的图象都经过点 $A (m ， 2)$ .

(1)、求k，m的值；

(2)、在图中画出正比例函数 $y = k x$ 的图象；并根据图象，直接写出不等式 $k x - \frac{6}{x} > 0$ 的解集.

查看试题解析
19. 濮阳是国家历史文化名城，曾出土距今6400多年的蚌塑龙形图案，被誉为“中华第一龙”.位于濮阳中心广场名为“中华第一龙”的龙形雕塑，其灵感就源自中国古代龙的形象.某校数学社团的同学们对龙形雕塑的高度进行了测量.如图，雕塑 $C D$ （含底座）垂直于地面，在雕塑两侧地面上相距35m的A，B两处分别测得 $∠ C A D = 42 °$ ， $∠ C B D = 58 °$ （A，D，B在同一条直线上）.求雕塑 $C D$ 的高度（结果保留一位小数）.参考数据： $s i n 42 ° \approx 0.67$ ， $c o s 42 ° \approx 0.74$ ， $t a n 42 ° \approx 0.90$ ， $s i n 58 ° \approx 0.85$ ， $c o s 58 ° \approx 0.53$ ， $t a n 58 ° \approx 1.60$ .

查看试题解析
20. 如图， $A B$ 为半圆O的直径，C为半圆O上一点，点D在 $\overset{⌢}{A C}$ 上、 $\overset{⌢}{C D} = \overset{⌢}{C B}$ ，连接 $A D$ ，过点C作 $A D$ 的垂线，交 $A D$ 的延长线于点E.

(1)、试判断 $C E$ 与 $⊙ O$ 的位置关系，并说明理由；

(2)、若 $A E = 3$ ， $A C = 2 \sqrt{3}$ ，求 $\overset{⌢}{C D}$ 的长.

查看试题解析
21. 问题情境：某市现在有两种用电收费方法：
分时电表
普通电表
峰时（8：00~21：00）
谷时（21：00到次日8：00）
电价0.55元/千瓦时
电价0.35元/千瓦时
电价0.52元/千瓦时
小明家所在的小区用的电表都换成了分时电表.
解决向题：

(1)、小明家第一季度电费为145元，用电总量为300千瓦时，求小明家第一季度的峰时用电量和谷时用电量；

(2)、设某家庭某月用电总量为a千瓦时（a为常数），其中谷时用电x千瓦时，用分时电表计价时总价为 $y_{1}$ 元，若采用普通电表计价时总价为 $y_{2}$ 元.
①分别写出 $y_{1}$ ， $y_{2}$ 与用电量的函数关系式（不要求写自变量的取值范围），并求出当 $\frac{x}{a}$ 满足什么条件时，家庭使用分时电表合算；
②根据（1）中的结果，分析小明家使用分时电表是否合算，并说明理由.

查看试题解析
22. 我们不妨约定：对于某一自变量为x的函数，若当 $x = m$ 时，其函数值也为m，则称点 $(m ， m)$ 为此函数的“不动点”.如：反比例函数 $y = \frac{1}{x}$ 有两个“不动点”，坐标分别为 $(1 ， 1)$ 和 $(- 1 ， - 1)$ .

(1)、一次函数 $y = 3 x - 1$ 的“不动点”坐标为；

(2)、若抛物线L： $y = a x^{2} - 2 a x + 2$ 上只有一个“不动点”A.
①求抛物线L的解析式和这个“不动点”A的坐标；
②在平面直角坐标系 $x O y$ 中，将抛物线L平移后，得到抛物线 $L^{'}$ ： $y = a x^{2} - 2 a x + 2 + n (n \neq 0)$ ，抛物线 $L^{'}$ 与y轴交于点B，连接 $O A$ ， $A B$ .若抛物线 $L^{'}$ 的顶点落在 $△ O A B$ 内部（不含边界），请直接写出n的取值范围.

查看试题解析
23. 数学课上，王老师出示了这样一个问题：如图1，在矩形 $A B C D$ 中， $A D = 2 A B$ ， E是 $A B$ 延长线上一点，且 $B E = A B$ ，连接 $D E$ ，交 $B C$ 于点M，以 $D E$ 为一边在 $D E$ 的左下方作正方形 $D E F G$ ，连接 $A M$ .试判断线段 $A M$ 与 $D E$ 的位置关系.

探究展示：小明发现， $A M$ 垂直平分 $D E$ ，并展示了如下的证明方法：

证明：∵ $B E = A B$ ， ∴ $A E = 2 A B$ .

∵ $A D = 2 A B$ ， ∴ $A D = A E$ .

∵四边形 $A B C D$ 是矩形，∴ $A D ∥ B C$ ，

∴ $\frac{E M}{D M} = \frac{E B}{A B}$ .（依据1）

∵ $B E = A B$ ， ∴ $\frac{E M}{D M} = 1$ ， ∴ $E M = D M$ .

即 $A M$ 是 $△ A D E$ 的 $D E$ 边上的中线，

又∵ $A D = A E$ ， ∴ $A M ⊥ D E$ ， .（依据2）

∴ $A M$ 垂直平分 $D E$ .

(1)、反思交流：
①上述证明过程中的“依据1”“依据2”分别是指什么？

②试判断图1中的点A是否在线段 $G F$ 的垂直平分线上，请直接回答，不必证明；

(2)、小颖受到小明的启发，继续进行探究，如图2，连接 $C E$ ，以 $C E$ 为一边在 $C E$ 的左下方作正方形 $C E F G$ ，发现点G在线段 $B C$ 的垂直平分线上，请你给出证明：

(3)、拓展应用：如图3，连接 $C E$ ，以 $C E$ 为一边在 $C E$ 的右上方作正方形 $C E F G$ ，分别以点B，C为圆心，m为半径作弧，两弧交于点M，连接 $M F$ .若 $M F = A B = 1$ ，请直接写出m的值.

查看试题解析

分时电表		普通电表
峰时（8：00~21：00）	谷时（21：00到次日8：00）
电价0.55元/千瓦时	电价0.35元/千瓦时	电价0.52元/千瓦时