河南省信阳市固始县2022年九年级下学期第一次适应性考试数学试卷

试卷更新日期：2022-04-29 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列有理数中最大的数是（）

A、0 B、 $- 1$ C、 $- \frac{1}{2}$ D、 $3^{- 1}$

查看试题解析
2. 2022年1月20日，河南省统计局公布2021年全省地区生产总值为58887.41亿元，同比增长6.3%.这里的近似数“58887.41亿”是精确到（）

A、百万位 B、亿位 C、万位 D、百分位

查看试题解析
3. 下列用相同的正方体堆放在一起组成的几何体中，主视图和左视图不相同的是（）

A、 B、 C、 D、

查看试题解析
4. 下列运算正确的是（）

A、 $2 x^{2} + 3 x^{3} = 5 x^{5}$ B、 $x^{3} \cdot x^{2} = x^{6}$ C、 $x^{6} \div x^{3} = x^{3}$ D、 ${(- 3 x)}^{2} = 6 x^{2}$

查看试题解析
5. 如图，已知 $A B ∥ D E$ ， $∠ B = 82 °$ ， $∠ C = 38 °$ ，则 $∠ D$ 等于（）

A、 $136 °$ B、 $130 °$ C、 $120 °$ D、 $112 °$

查看试题解析
6. 已知点 $A (x_{1} ， - 1)$ ， $B (x_{2} ， 2)$ ， $C (x_{3} ， 3)$ 都在反比例函数 $y = - \frac{1}{x}$ 的图象上，那么 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 的大小关系是（）

A、 $x_{1} > x_{2} > x_{3}$ B、 $x_{1} > x_{3} > x_{2}$ C、 $x_{3} > x_{2} > x_{1}$ D、 $x_{2} > x_{3} > x_{1}$

查看试题解析
7. 西峡猕猴桃，河南省西峡县特产，中国国家地理标志产品.种植户小王新摘了一批猕猴桃，这些猕猴桃的质量的平均数和方差分别是 $\bar{x}$ ， $s^{2}$ ，小王从中选出质量大且均匀的猕猴桃作为一等品销售，一等品猕猴桃的质量的平均数和方差分别为 $\bar{x_{1}}$ ， $s_{1}^{2}$ ，则下列结论一定成立的是（）

A、 $\bar{x} = \bar{x_{1}}$ B、 $\bar{x} > \bar{x_{1}}$ C、 $s^{2} > s_{1}^{2}$ D、 $s^{2} < s_{1}^{2}$

查看试题解析
8. 对于实数m，n，定义一种运算“ $※$ ”为 $m ※ n = m^{2} + m n$ ，例如， $5 ※ 3 = 5^{2} + 5 \times 3 = 40$ 那么不等式组 ${\begin{array}{l} (- 2) ※ x > 0 \\ 1 ※ x \geq 0 \end{array}$ 的解集在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
9. 如图，边长为2的正六边形 $A B C D E F$ 放置于平面直角坐标系中，边 $A F$ 在x轴的负半轴上，顶点B在y轴正半轴上，将正六边形 $A B C D E F$ 绕坐标原点O旋转 $90 °$ 后，顶点D恰好落在双曲线上，那么该双曲线是（）

A、 $y = - \frac{6 \sqrt{3}}{x}$ B、 $y = \frac{6 \sqrt{3}}{x}$ C、 $y = - \frac{3 \sqrt{3}}{x}$ D、 $y = \frac{3 \sqrt{3}}{x}$

查看试题解析
10. 如图，已知 $△ A B C$ ， $∠ C = 90 °$ ，按以下步骤作图：①以点A为圆心，以适当长为半径画弧，分别交边 $A C$ ， $A B$ 于点M，N；②分别以M，N为圆心，以大于 $\frac{1}{2} M N$ 的长为半径画弧，两弧在 $△ A B C$ 的内部相交于点P；③作射线 $A P$ 交 $B C$ 于点D；④分别以A，D为圆心，以大于 $\frac{1}{2} A D$ 的长为半径画弧，两弧相交于点G，H；⑤作直线 $G H$ ，分别交 $A C$ ， $A B$ 于点E，F，若 $A F = 3$ ， $C E = 1$ ，则 $△ A B C$ 的面积是（）

A、 $2 \sqrt{2}$ B、 $8 \sqrt{2}$ C、 $16 \sqrt{2}$ D、 $32 \sqrt{2}$

查看试题解析

二、填空题

11. 若 $\frac{x}{3} = \frac{y}{5} = \frac{z}{7}$ ，则 $\frac{x - y + z}{x + y - z}$ =.

查看试题解析
12. 若关于x的分式方程 $\frac{m - 1}{x - 1} = 2$ 的解为正数，则m的取值范围是.

查看试题解析
13. 2022年冬奥会吉祥物为“冰墩墩”，冬残奥会吉祥物为“雪容融”.如图，现有三张正面印有吉祥物的不透明卡片，卡片除正面图案不同外，其余均相同，其中两张正面印有冰墩墩图案，一张正面印有雪容融图案，将三张卡片正面向下洗匀，从中随机抽取一张卡片，记下图案后正面向下放回，洗匀后再从中随机抽取一张卡片，则抽出的两张卡片图案都是冰墩墩的概率是.

查看试题解析
14. 如图，已知 $△ A B C$ 中， $∠ A B C = 35 °$ ， $∠ B A C = 45 °$ ， $B C = 2$ ，则经过A，B，C三点的 $\overset{⌢}{A C B}$ 的长度为.

查看试题解析
15. “希望小组”的同学们利用课余时间对“纸片中的折叠问题”进行了探究.如图，在 $△ A B C$ 中， $A B = A C = 3$ ， $∠ B = 30 °$ ，点D是 $B C$ 边上不与端点B，C重合的一个动点，第一步，将 $△ A B D$ 沿 $A D$ 折叠，点B的对应点为 $B^{'}$ ；第二步，将 $△ A D B^{'}$ 沿 $A B^{'}$ 折叠，点D的对应点为 $D^{'}$ ，当直线 $D D^{'}$ 过 $△ A B C$ 的一个顶点时，线段 $B D$ 的长度为.

查看试题解析

三、解答题

16. 化简与计算：

(1)、 $| 1 - \sqrt{2} | + 2 c o s 45 ° - \sqrt{8}$ ；

(2)、 $(x - \frac{2 x - 1}{x}) \div \frac{x^{2} - 1}{x}$

查看试题解析
17. 为落实教育部“双减”政策，某市从2021年9月起，各中小学全面开展课后延时服务.为了了解该市甲、乙两所中学延时服务的情况，在这两所学校分别随机抽查了100名家长进行问卷调查.家长对延时服务的综合评分记为x，将所得数据分为5个等级（A“很满意”： $90 \leq x \leq 100$ ；B“满意”： $80 \leq x < 90$ ； $C$ “比较满意”： $70 \leq x < 80$ ；D“不太满意”： $60 \leq x < 70$ ；E“不满意”： $0 \leq x < 60$ ），将数据进行整理后，得到如下统计图和统计表.
①甲中学延时服务得分的扇形统计图
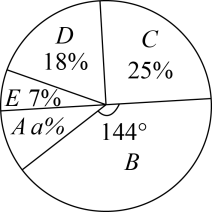
②乙中学延时服务得分频数分布统计表
等级
满意度
得分
频数
A
很满意
$90 \leq x \leq 100$
15
B
满意
$80 \leq x < 90$
C
比较满意
$70 \leq x < 80$
30
D
不太满意
$60 \leq x < 70$
10
E
不满意
$0 \leq x < 60$
5
③甲、乙两中学延时服务得分的平均数、中位数、众数如下表：
学校
平均数
中位数
众数
甲
78
79.5
80
乙
80
$b$
85
④乙中学的等级“B”的分数从高到低排列，排在最后的10个数据分别是：84，84，83，83，83，81，80，80，80，80.
请你根据以上信息，回答下列问题：

(1)、直接写出a和b的值；

(2)、课后延时服务综合得分在70分及以上为合格，请你估计甲中学3000名家长中认为该校课后延时服务合格的人数；

(3)、小明说：“乙中学的课后延时服务比甲中学好”，你同意小明的说法吗？请写出一条理由.

查看试题解析
18. 如图，点C是以 $A B$ 为直径的半圆O上一动点，作半径 $O A$ 的垂直平分线交 $O A$ 于点F，交 $A C$ 于点E，交切线 $C D$ 于点D.

(1)、判断 $△ C D E$ 的形状，并说明理由；

(2)、若 $⊙ O$ 的半径是2， $c o s B = \frac{1}{4}$ ，求 $C E$ 的长.

查看试题解析
19. 如图，某校大礼堂前墙 $A B$ 上悬挂宣传标语 $A D$ .为了测量标语 $A D$ 的高度，小冬站在大礼堂正前方与点B相距8米的点C处，测得标语上端点A的仰角为 $55 °$ ，前进2米正好走到台阶M处，台阶高0.2米，在台阶的边沿点E处测得标语下端点D的仰角为 $60 °$ ，求标语 $A D$ 的高度.（结果精确到0.01米，参考数据： $s i n 55 ° \approx 0.82$ ， $c o s 55 ° \approx 0.57$ ， $t a n 55 ° \approx 1.43$ ， $\sqrt{3} \approx 1.73$ ）

查看试题解析
20. 在平面直角坐标系 $x O y$ 中，点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ 在抛物线 $y = a x^{2} - 2 a x + 1 (a > 0)$ 上，其中 $x_{1} < x_{2}$

(1)、求抛物线的对称轴；

(2)、若 $x_{1} + x_{2} = 2 - a$ ，比较 $y_{1}$ 与 $y_{2}$ 的大小关系，并说明理由.

查看试题解析
21. 喜万家超市以原价为20元/瓶的价格对外销售某种洗手液，为了减少库存，决定降价销售，经过两次降价后，售价为16.2元/瓶.

(1)、求平均每次降价的百分率；

(2)、为确保新学期开学工作安全、卫生、健康、有序，某学校决定购买一批洗手液（超过200瓶）.超市对购买量大的客户有优惠措施，在16.2元/瓶的基础上推出方案一：每瓶打九折；方案二：不超过200瓶的部分不打折，超过200瓶的部分打八折，学校应该选择哪种方案更省钱（只能选择一种）？请说明理由.

查看试题解析

22. 九（1）班数学兴趣小组的同学参照学习函数的过程与方法，探究函数

y = {\begin{array}{l} x^{2} - 4 (x < 3) \\ \frac{5}{x - 2} (x \geq 3) \end{array}

的图象与性质，他们的探究过程如下，请你补充完整.

(1)、列表：

x	…	$- 3$	$- 2$	$- 1$	0	1	2	3	4	5	6	7	…
y	…	m	0	$- 3$	$- 4$	$- 3$	0	5	n	$\frac{5}{3}$	$\frac{5}{4}$	1	…

表中m= ， n=.

(2)、描点、连线：

如图，在平面直角坐标系中，根据上表中数据以自变量x的值为横坐标，以相应的函数值y为纵坐标，描出了部分对应点，请你描出剩余的点，并画出该函数的图象.

(3)、探究性质，解决问题：

①试写出该函数的一条性质：；

②当 $y \geq 1$ 时，函数 $y = {\begin{array}{l} x^{2} - 4 (x < 3) ， \\ \frac{5}{x - 2} (x \geq 3) \end{array}$ 的自变量x的取值范围是；

③若直线 $y = k (x + 6) - 4$ 与函数 $y = {\begin{array}{l} x^{2} - 4 (x < 3) ， \\ \frac{5}{x - 2} (x \geq 3) \end{array}$ 的图象有三个不同的交点，请直接写出k的取值范围.

查看试题解析

23. 数学综合与实践课上，同学们以“三角形的旋转”为主题开展探究活动，如图，小东同学把等腰直角三角板 $A B C$ 的直角顶点C绕着直角三角板 $D E F$ 的斜边中点旋转，其中 $∠ E = 30 °$ ，直线 $A C$ ， $D F$ 相交于点G，边 $B C$ 与 $D E$ 相交于点H.

(1)、如图①，当 $B C ⊥ D E$ 时，线段 $C G$ 与 $C H$ 的数量关系是；

(2)、将图①中的 $△ A B C$ 旋转到如图②所示的位置，请判断线段 $C G$ 与 $C H$ 的数量关系是否发生变化，并说明理由.

(3)、在（2）的情况下，若 $△ A B C$ 绕点C旋转时，边 $B C$ 与 $D E$ 的交点H始终在线段 $D E$ 上，连接 $G H$ ，若 $D F = 16$ ， $S_{△ C G H} = 50 \sqrt{3}$ ，请直接写出线段 $D H$ 的长度.

查看试题解析

等级	满意度	得分	频数
A	很满意	$90 \leq x \leq 100$	15
B	满意	$80 \leq x < 90$
C	比较满意	$70 \leq x < 80$	30
D	不太满意	$60 \leq x < 70$	10
E	不满意	$0 \leq x < 60$	5

学校	平均数	中位数	众数
甲	78	79.5	80
乙	80	$b$	85