广西桂林市灌阳县2022年中考第一次模拟考试数学试卷

试卷更新日期：2022-04-29 类型：中考模拟

进入出卷网下载

一、单选题

1. 实数 $\frac{1}{3}$ ， $- \sqrt{3}$ ， 2，-6中，为负整数的是（）

A、 $\frac{1}{3}$ B、 $- \sqrt{3}$ C、2 D、- 6

查看试题解析
2. 下列各式中，与 $2 a^{2} b$ 为同类项的是（）

A、-2ab B、-2a²b C、2ab D、2a²

查看试题解析
3. 一元二次方程 $x^{2} - 2 x + 1 = 0$ 的解为（）

A、x＝0 B、x＝1 C、x＝-1 D、x＝-2

查看试题解析
4. 如图，在⊙O中， $\overset{⌢}{A B} = \overset{⌢}{C D}$ ， ∠1＝45°，则∠2的度数为(　　)

A、60° B、30° C、45° D、40°

查看试题解析
5. 如图所示为几何体的平面展开图，其对应的几何体名称为（）

A、正方体 B、圆锥 C、四棱柱 D、三棱柱

查看试题解析
6. 下列二次根式中，最简二次根式的是（）

A、 $\sqrt{\frac{1}{5}}$ B、 $\sqrt{0.5}$ C、 $\sqrt{5}$ D、 $\sqrt{50}$

查看试题解析
7. 如图是一个正方体的表面展开图，如果对面上所标的两个数互为相反数，那么图中x的值是（）．

A、 $- 3$ B、 $3$ C、 $2$ D、 $8$

查看试题解析
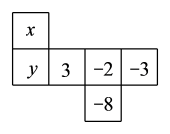8. 圆的半径是7cm，如果圆心与直线上某一点的距离是6.5cm，那么该直线和圆的位置关系是（）

A、相离 B、相切 C、相交 D、相交或相切

查看试题解析
9. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
10. 将抛物线 $y = x^{2} - 2 x + 3$ 向上平移2个单位长度，得到的抛物线解析式为（）

A、 $y = (x - 1)^{2} + 4$ B、 $y = (x - 4)^{2} + 4$ C、 $y = (x + 2)^{2} + 6$ D、 $y = (x - 4)^{2} + 6$

查看试题解析
11. 如图，在⊙O中，直径CD⊥弦AB，则下列结论中正确的是（）

A、AC=AB B、∠C= $\frac{1}{2}$ ∠BOD C、∠C=∠B D、∠A=∠B0D

查看试题解析
12. 如图，圆O的半径为1，AD，BC是⊙O的两条互相垂直的直径，点P从点O出发（P点与O点不重合），沿O→C→D的路线运动，设AP=x，sin∠APB=y，那么y与x之间的关系图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

13. 5的相反数是．

查看试题解析
14. 分解因式：x² －x＝.

查看试题解析
15. “清明时节雨纷纷”是事件．(填“必然”“不可能”或“随机”)

查看试题解析
16. 如图，若抛物线y=ax²+bx+c上的P（4，0），Q两点关于它的对称轴x=1对称，则Q点的坐标为．

查看试题解析
17. 点P(2m－3，1)在反比例函数y＝ $\frac{1}{x}$ 的图象上，则m＝．

查看试题解析
18. 如图，AB为⊙O的切线，切点为B，连接AO，AO与⊙O交于点C，BD为⊙O的直径，连接CD，若∠A＝30°，⊙O的半径为2，则图中阴影部分的面积为（结果保留π）

查看试题解析

三、解答题

19. 计算： $s i n 3 0^{o} + (- 2)^{0}$ ．

查看试题解析
20. 已知△ABC的顶点A、B、C在格点上，按下列要求在网格中画图．

( 1 )△ABC绕点C顺时针旋转90°得到△A₁B₁C；

( 2 )画△A₁B₁C关于点O的中心对称图形△A₂B₂C₂ ．

查看试题解析
21. 先化简再求值： $（ x - \frac{3 x}{x + 1}) \div \frac{x - 2}{x^{2} + 2 x + 1}$ ，其中x满足 $x^{2} + x - 2 = 0$

查看试题解析
22. 嫦娥、神舟、北斗、天问被称为中国航天的“四大天王”.2020年“北斗”组网、“天问”问天、“嫦五”探月，一个个好消息从太空传来，照亮了中国航天界的未来!小玲对航空航天非常感兴趣，她收集到了嫦娥五号、神舟十一号、北斗三号、天问一号的模型图，依次制成编号为A、B、C、D的四张卡片（背面完全相同），将这四张卡片背面朝上，洗匀放好．

(1)、小玲从中随机抽取一张卡片是“北斗三号”的概率为；

(2)、小玲从四张卡片中随机抽取一张卡片（不放回）．再从余下的卡片中随机抽取一张，请用列表或画树状图的方法求抽到的两张卡片恰好是编号为A（嫦娘五号）和D（天问一号）的概率．

查看试题解析
23. 已知点E、F分别为平行四边形ABCD的边AD、BC的中点，求证：四边形EBFD为平行四边形.

查看试题解析
24. 某学校为了改进全校师生的饮水质量．需要安装A型净水器与B型净水器，已知每台A型净水器比B型净水器售价贵2000元，且安装A型净水器的数量是B型净水器数量的 $\frac{4}{5}$ ，学校分别购买A型与B型净水器的费用都是20万元．求每台A型净水器和每台B型净水器的售价分别为多少元？

查看试题解析
25. 已知：△ABC是边长为4的等边三角形，点O在边AB上，⊙O过点B且分别与边AB，BC相交于点D，E，EF⊥AC，垂足为F．

(1)、求证：直线EF是⊙O的切线；

(2)、当直线DF与⊙O相切时，求⊙O的半径．

查看试题解析
26. 如图，在平面直角坐标系xOy中，AB在x轴上，以AB为直径的半圆⊙O′与y轴正半轴交于点C，连接BC，AC．CD是半圆⊙O′的切线，AD⊥CD于点D．

(1)、求证：∠CAD =∠CAB；

(2)、已知抛物线y = ax² + bx + c过A、B、C三点，AB = 10，tan∠CAD = $\frac{1}{2}$ ：
① 求抛物线的解析式；
② 判断抛物线的顶点E是否在直线CD上，并说明理由；

(3)、在抛物线上是否存在一点P，使四边形PBCA是直角梯形，请说明理由．

查看试题解析