广西崇左市江州区2022年中考模拟考试数学试题(一)
试卷更新日期:2022-04-29 类型:中考模拟
一、单选题
-
1. 下列各数中是无理数的是( )A、3.14 B、﹣ C、0.56 D、2. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
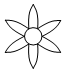 B、
B、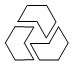 C、
C、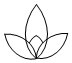 D、
D、 3. 2020年5月22日,李克强总理在政府工作报告中指出:三大攻坚战取得关键进展,农村贫困人口减少 人,贫困发生率降至 脱贫攻坚取得决定性成就.将数字 用科学记数法表示为( )A、 B、 C、 D、4. 下列调查中,最适合采用全面调查的是( )A、对全国中学生视力和用眼卫生情况的调查 B、对某班学生的身高情况的调查 C、对某鞋厂生产的鞋底能承受的弯折次数的调查 D、对某池塘中现有鱼的数量的调查5. 已知⊙O的半径为3,点P到圆心O的距离为4,则点P( )A、在⊙O内 B、在⊙O上 C、在⊙O外 D、无法确定6. 下列运算正确的是( )A、(﹣ab2)3=﹣a3b6 B、2a+3a=5a2 C、(a+b)2 = a2+b2 D、a2•a3=a67. 设a=+2,则( )A、2 <a<3 B、3<a<4 C、4 <a<5 D、5 <a<68. △ABC与 △DEF位似,点O为位似中心,已知OA=AD, 则△ABC与 △DEF 的面积比为( )
3. 2020年5月22日,李克强总理在政府工作报告中指出:三大攻坚战取得关键进展,农村贫困人口减少 人,贫困发生率降至 脱贫攻坚取得决定性成就.将数字 用科学记数法表示为( )A、 B、 C、 D、4. 下列调查中,最适合采用全面调查的是( )A、对全国中学生视力和用眼卫生情况的调查 B、对某班学生的身高情况的调查 C、对某鞋厂生产的鞋底能承受的弯折次数的调查 D、对某池塘中现有鱼的数量的调查5. 已知⊙O的半径为3,点P到圆心O的距离为4,则点P( )A、在⊙O内 B、在⊙O上 C、在⊙O外 D、无法确定6. 下列运算正确的是( )A、(﹣ab2)3=﹣a3b6 B、2a+3a=5a2 C、(a+b)2 = a2+b2 D、a2•a3=a67. 设a=+2,则( )A、2 <a<3 B、3<a<4 C、4 <a<5 D、5 <a<68. △ABC与 △DEF位似,点O为位似中心,已知OA=AD, 则△ABC与 △DEF 的面积比为( )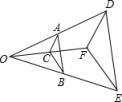 A、1:2 B、2:1 C、1:3 D、1:49. 如图,在 中, ,观察图中尺规作图的痕迹,则 的度数为( )
A、1:2 B、2:1 C、1:3 D、1:49. 如图,在 中, ,观察图中尺规作图的痕迹,则 的度数为( )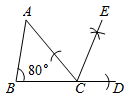 A、 B、 C、 D、10. 《九章算术》勾股章有一问题,其意思是:现有一竖立着的木柱,在木柱上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵着绳索退行,在离木柱根部8尺处时绳索用尽,请问绳索有多长?若设绳索长度为x尺,根据题意,可列方程为 ( )A、 B、 C、 D、11. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=4,S菱形ABCD=24,则OH的长为( )
A、 B、 C、 D、10. 《九章算术》勾股章有一问题,其意思是:现有一竖立着的木柱,在木柱上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵着绳索退行,在离木柱根部8尺处时绳索用尽,请问绳索有多长?若设绳索长度为x尺,根据题意,可列方程为 ( )A、 B、 C、 D、11. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=4,S菱形ABCD=24,则OH的长为( )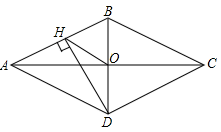 A、.2 B、3 C、 D、12. 如图,点A在反比例函数y=(x>0)的图象上,点B在x轴负半轴上,直线AB交y轴于点C,若 , △AOB的面积为6,则k的值为( )
A、.2 B、3 C、 D、12. 如图,点A在反比例函数y=(x>0)的图象上,点B在x轴负半轴上,直线AB交y轴于点C,若 , △AOB的面积为6,则k的值为( )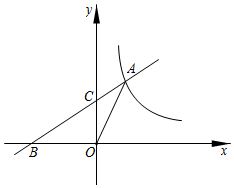 A、2 B、4 C、5 D、6
A、2 B、4 C、5 D、6二、填空题
-
13. 函数的自变量x的取值范围为 .
14. 分解因式:a3﹣ab2= .15. 如图,在矩形 中,对角线 , 相交于点O,已知 , ,则 的长为cm.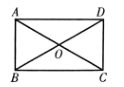 16. 关于x的一元二次方程有两个相等的实数根,则k的值为.17. 现有一个半径为8cm的半圆形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计).该圆锥底面圆的半径为cm.18. 如图,正方形ABCD边长为2,F为BC上一动点,作DE⊥AF于E,连接CE.当△CDE是以CD为腰的等腰三角形时,DE的长为 .
16. 关于x的一元二次方程有两个相等的实数根,则k的值为.17. 现有一个半径为8cm的半圆形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计).该圆锥底面圆的半径为cm.18. 如图,正方形ABCD边长为2,F为BC上一动点,作DE⊥AF于E,连接CE.当△CDE是以CD为腰的等腰三角形时,DE的长为 .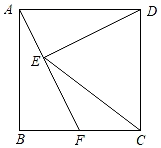
三、解答题
-
19. .20. 解不等式组: , 并把解集在数轴上表示出来.21. 如图,在直角坐标系中,已知ABC的三个顶点坐标分别为A(1,3),B(4,2),C(3,4).
 (1)、请画出ABC关于原点O对称的A1B1C1;(2)、请画出ABC绕点O逆时针旋转90°后的A2B2C2 , 并直接写出点B旋转到点B2所经过的路径长.22. 为落实关于开展中小学课后服务工作的要求,某学校开设了四门校本课程供学生选择:A、趣味数学; B、博乐阅读;C、快乐英语;D、硬笔书法.某年级共有100名学生选择了A课程,为了解本年级选择A课程学生的学习情况,从这100名学生中随机抽取了30名学生进行测试,将他们的成绩(百分制)分成六组,绘制成频数分布直方图.
(1)、请画出ABC关于原点O对称的A1B1C1;(2)、请画出ABC绕点O逆时针旋转90°后的A2B2C2 , 并直接写出点B旋转到点B2所经过的路径长.22. 为落实关于开展中小学课后服务工作的要求,某学校开设了四门校本课程供学生选择:A、趣味数学; B、博乐阅读;C、快乐英语;D、硬笔书法.某年级共有100名学生选择了A课程,为了解本年级选择A课程学生的学习情况,从这100名学生中随机抽取了30名学生进行测试,将他们的成绩(百分制)分成六组,绘制成频数分布直方图.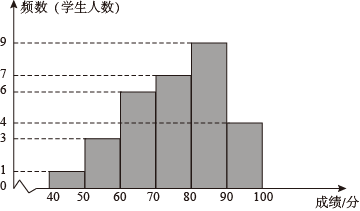 (1)、已知70≤x<80这组的数据为72,73,74,75,76,76,79.则这组数据的中位数、众数分别是多少;(2)、根据题中信息,估计该年级选择A课程学生成绩在80≤x<90的总人数;(3)、该年级每名学生选两门不同的课程,小张和小王在选课程的过程中,若第一次都选了课程C,那么他俩第二次同时选择课程A或课程B的概率是多少?请用列表法或画树状图的方法加以说明.23. 如图,⊙O的直径AB=10,∠ACB的平分线CD交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD.
(1)、已知70≤x<80这组的数据为72,73,74,75,76,76,79.则这组数据的中位数、众数分别是多少;(2)、根据题中信息,估计该年级选择A课程学生成绩在80≤x<90的总人数;(3)、该年级每名学生选两门不同的课程,小张和小王在选课程的过程中,若第一次都选了课程C,那么他俩第二次同时选择课程A或课程B的概率是多少?请用列表法或画树状图的方法加以说明.23. 如图,⊙O的直径AB=10,∠ACB的平分线CD交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD.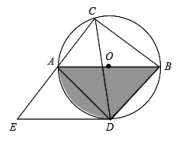 (1)、求由AB,BD,弧AD围成的阴影部分的面积;(2)、求证:DE是⊙O的切线.24. 我市九年级学生安全有序开学复课.为切实做好疫情防控工作,开学前夕,我市某校准备在民联药店购买口罩和水银体温计发放给每个学生.已知每盒口罩有100只,每盒水银体温计有10支,每盒口罩价格比每盒水银体温计价格贵150元.用1200元购买口罩盒数与用300元购买水银体温计所得盒数相同.(1)、求每盒口罩和每盒水银体温计的价格各是多少元?(2)、如果给每位学生发放2只口罩和1支水银体温计,且口罩和水银体温计均整盒购买.设购买口罩m盒(m为正整数),则购买水银体温计多少盒能和口罩刚好配套?请用含m的代数式表示;(3)、在民联药店累计购医用品超过1800元后,超出1800元的部分可享受八折优惠.该校按(2)中的配套方案购买,共支付w元,求w关于m的函数关系式.25. 【阅读理解】截长补短法,是初中数学几何题中一种辅助线的添加方法.截长就是在长边上截取一条线段与某一短边相等,补短是通过在一条短边上延长一条线段与另一短边相等,从而解决问题.
(1)、求由AB,BD,弧AD围成的阴影部分的面积;(2)、求证:DE是⊙O的切线.24. 我市九年级学生安全有序开学复课.为切实做好疫情防控工作,开学前夕,我市某校准备在民联药店购买口罩和水银体温计发放给每个学生.已知每盒口罩有100只,每盒水银体温计有10支,每盒口罩价格比每盒水银体温计价格贵150元.用1200元购买口罩盒数与用300元购买水银体温计所得盒数相同.(1)、求每盒口罩和每盒水银体温计的价格各是多少元?(2)、如果给每位学生发放2只口罩和1支水银体温计,且口罩和水银体温计均整盒购买.设购买口罩m盒(m为正整数),则购买水银体温计多少盒能和口罩刚好配套?请用含m的代数式表示;(3)、在民联药店累计购医用品超过1800元后,超出1800元的部分可享受八折优惠.该校按(2)中的配套方案购买,共支付w元,求w关于m的函数关系式.25. 【阅读理解】截长补短法,是初中数学几何题中一种辅助线的添加方法.截长就是在长边上截取一条线段与某一短边相等,补短是通过在一条短边上延长一条线段与另一短边相等,从而解决问题.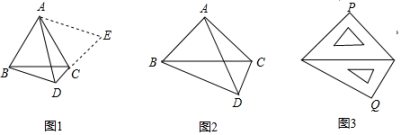 (1)、如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.
(1)、如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.解题思路:延长DC到点E,使CE=BD,连接AE,根据∠BAC+∠BDC=180°,可证∠ABD=∠ACE易证得△ABD≌△ACE,得出△ADE是等边三角形,所以AD=DE,从而探寻线段DA、DB、DC之间的数量关系.根据上述解题思路,请直接写出DA、DB、DC之间的数量关系是;
(2)、【拓展延伸】
如图2,在Rt△ABC中,∠BAC=90°,AB=AC.若点D是边BC下方一点,∠BDC=90°,探索线段DA、DB、DC之间的数量关系,并说明理由;(3)、【知识应用】
如图3,两块斜边长都为4cm的三角板,把斜边重叠摆放在一起,则两块三角板的直角顶点之间的距离PQ的长为cm.26. 如图,抛物线与x轴交于A,B两点,与y轴交于C点.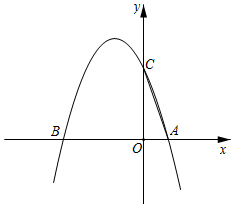 (1)、求点B,C的坐标;(2)、在第二象限内的抛物线上确定一点P,使四边形PBOC的面积最大,求出点P的坐标;(3)、点M为抛物线上一动点,x轴上是否存在一点Q,使以B、C、M、Q为顶点的四边形是平行四边形,若存在,请直接写出Q点的坐标;若不存在,请说明理由.
(1)、求点B,C的坐标;(2)、在第二象限内的抛物线上确定一点P,使四边形PBOC的面积最大,求出点P的坐标;(3)、点M为抛物线上一动点,x轴上是否存在一点Q,使以B、C、M、Q为顶点的四边形是平行四边形,若存在,请直接写出Q点的坐标;若不存在,请说明理由.