广西崇左市扶绥县2022年中考一模数学试卷
试卷更新日期:2022-04-29 类型:中考模拟
一、单选题
-
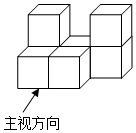
1. 的相反数是( )A、-3 B、+3 C、 D、-0.32. 如图所示的几何体是由7个大小相同的正方体块搭成,它的主视图是( )
 A、
A、 B、
B、 C、
C、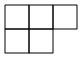 D、
D、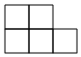 3. 2022 年冬奥会由北京和张家口两市联合承办.北京到张家口的自驾距离约为196000 米.196000 用科学记数法表示应为( )A、 1.96×105 B、19.6×104 C、1.96×106 D、0.196×1064. 如图,小球从A口往下落,在每个交叉口都有向左或向右两种可能,且可能性相同,则小球最终从G口落出的概率为( )
3. 2022 年冬奥会由北京和张家口两市联合承办.北京到张家口的自驾距离约为196000 米.196000 用科学记数法表示应为( )A、 1.96×105 B、19.6×104 C、1.96×106 D、0.196×1064. 如图,小球从A口往下落,在每个交叉口都有向左或向右两种可能,且可能性相同,则小球最终从G口落出的概率为( ) A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 关于方程的根的说法中,正确的是( )A、没有实数根 B、两实数根的和为 C、有两个不相等的实数根 D、两实数根的积为7. 直角坐标系中的点A(2,-3)关于x轴对称的点B的坐标( )A、(2,3 ) B、(2,-3) C、(-2,3) D、(-2,-3)8. 如图,是的内接三角形, , , 过点B作BD∥AC,交于点D,连接 , 则的大小为( )
A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 关于方程的根的说法中,正确的是( )A、没有实数根 B、两实数根的和为 C、有两个不相等的实数根 D、两实数根的积为7. 直角坐标系中的点A(2,-3)关于x轴对称的点B的坐标( )A、(2,3 ) B、(2,-3) C、(-2,3) D、(-2,-3)8. 如图,是的内接三角形, , , 过点B作BD∥AC,交于点D,连接 , 则的大小为( )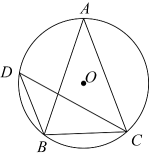 A、 B、 C、 D、9. 反比例函数 的图象分别位于第二、四象限,则直线 不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为( )
A、 B、 C、 D、9. 反比例函数 的图象分别位于第二、四象限,则直线 不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为( )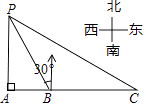 A、40海里 B、60海里 C、20 海里 D、40 海里11. 一个自然数的立方,可以分裂成若干个连续奇数的和.例如: , 和分别可以“分裂”成2个,3个和4个连续奇数的和,即 , , , , 若也按照此规律来进行“分裂”,则“分裂”出的奇数中,最大的奇数是( )A、 B、 C、 D、12. 如图,在平面直角坐标系中,抛物线的顶点为A点,且与x轴的正半轴交于点B,P点是该抛物线对称轴上的一点,则的最小值为( )
A、40海里 B、60海里 C、20 海里 D、40 海里11. 一个自然数的立方,可以分裂成若干个连续奇数的和.例如: , 和分别可以“分裂”成2个,3个和4个连续奇数的和,即 , , , , 若也按照此规律来进行“分裂”,则“分裂”出的奇数中,最大的奇数是( )A、 B、 C、 D、12. 如图,在平面直角坐标系中,抛物线的顶点为A点,且与x轴的正半轴交于点B,P点是该抛物线对称轴上的一点,则的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 若代数式在实数范围内有意义,x的取值范围是.14. 分解因式:15. 如图是小李在新冠疫情期间连续两周居家健康检测记录的体温情况折线统计图,记第一周体温的方差为 , 第二周体温的方差为 , 则选填“>”、“<”或“=”.
 16. 如图,已知 , , 观察图中尺规作图的痕迹,则.
16. 如图,已知 , , 观察图中尺规作图的痕迹,则. 17. 如图,把矩形纸片ABCD分割成矩形纸片ABFE和正方形纸片EFCD后,分别裁出半径最大的圆和扇形CDF,若恰好能作为一个圆锥的底面和侧面,则.
17. 如图,把矩形纸片ABCD分割成矩形纸片ABFE和正方形纸片EFCD后,分别裁出半径最大的圆和扇形CDF,若恰好能作为一个圆锥的底面和侧面,则. 18. 如图,已知正方形边长为2,E为边上一点,将以点A为中心按顺时针方向旋转得到 , 连接 , 分别交 , 于点M,N.若 , 则.
18. 如图,已知正方形边长为2,E为边上一点,将以点A为中心按顺时针方向旋转得到 , 连接 , 分别交 , 于点M,N.若 , 则.
三、解答题
-
19. 计算:.20. 解分式方程:.21. 如图,在边长为1个单位长度的小正方形组成的网格中,三个顶点的坐标分别为 , , .

( 1 )请画出关于原点O成中心对称的;
( 2 )请画出将绕点逆时针旋转后得到的;
( 3 )在(2)的条件下,求线段扫过的面积(结果保留.
22. 某市各中小学为落实教育部政策,全面开展课后延时服务.市教育局为了解该市中学延时服务的情况,随机抽查甲、乙两所中学各名家长进行问卷调查.家长对延时服务的综合评分记为x,将所得数据分为5组(“很满意”:;“满意”:;“比较满意”:;“不太满意”:;“不满意”: , 市教育局将数据进行分析后,得到如下部分信息: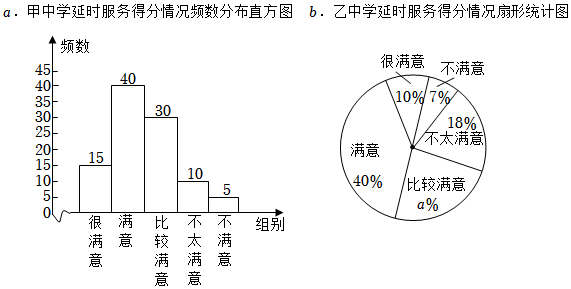
c.甲、乙两所中学延时服务得分的平均数、中位数、众数如表:
学校
平均数
中位数
众数
甲
乙
d.甲中学“满意”组的分数从高到低排列,排在最后的个数分别是: , , , , , , , , ,
请你根据以上信息,回答下列问题:
(1)、直接写出a和m的值;(2)、根据以上数据,你认为哪所中学的延时服务开展得更好?并说明理由一条即可;(3)、市教育局指出:延时服务综合得分在分及以上才算合格,请你估计乙中学名家长中认为该校延时服务合格的人数.23. 如图、在菱形中,对角线 , 相交于点过点D作对角线的垂线交的延长线于点E.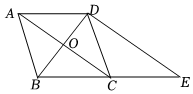 (1)、求证:四边形是平行四边形;(2)、若 , , 求的周长.24. 如图,在一次足球比赛中,守门员在地面 处将球踢出,一运动员在离守门员8米的 处发现球在自己头上的正上方4米处达到最高点 ,球落地后又一次弹起.据实验测算,足球在空中运行的路线是一条抛物线,在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)、求证:四边形是平行四边形;(2)、若 , , 求的周长.24. 如图,在一次足球比赛中,守门员在地面 处将球踢出,一运动员在离守门员8米的 处发现球在自己头上的正上方4米处达到最高点 ,球落地后又一次弹起.据实验测算,足球在空中运行的路线是一条抛物线,在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半. (1)、求足球第一次落地之前的运动路线的函数表达式及第一次落地点 和守门员(点 )的距离;(2)、运动员(点 )要抢到第二个落点 ,他应再向前跑多少米?(假设点 、 、 、 在同一条直线上,结果保留根号)
(1)、求足球第一次落地之前的运动路线的函数表达式及第一次落地点 和守门员(点 )的距离;(2)、运动员(点 )要抢到第二个落点 ,他应再向前跑多少米?(假设点 、 、 、 在同一条直线上,结果保留根号)