上海市普陀区2021-2022学年九年级下学期期中数学试题

试卷更新日期：2022-04-29 类型：期中考试

进入出卷网下载

一、单选题

1. 多边形的外角和等于（）

A、360° B、270° C、180° D、90°．

查看试题解析
2. 在平面直角坐标系中，直线y=x+1不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 如图，直线l₁//l₂ ，如果∠1=25°，∠2=20°，那么∠3的度数是（）

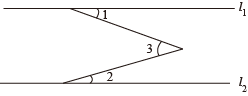A、55° B、45° C、40° D、35°

查看试题解析
4. 已知 $| \vec{a} | = 1$ ， $| \vec{b} | = 2$ ，且 $\vec{b}$ 与 $\vec{a}$ 的方向相反，那么下列结论中正确的是（）

A、 $\vec{a} = 2 \vec{b}$ B、 $\vec{a} = - 2 \vec{b}$ C、 $\vec{b} = 2 \vec{a}$ D、 $\vec{b} = - 2 \vec{a}$

查看试题解析
5. 如图，已知直线l₁//l₂//l₃ ，它们依次交直线l₄、l₅ ，于点A、C、E和点B、D、F，下列比例式中正确的是（）

A、 $\frac{A C}{A B} = \frac{C D}{B F}$ B、 $\frac{A B}{C D} = \frac{C D}{E F}$ C、 $\frac{A C}{A E} = \frac{B D}{B F}$ D、 $\frac{A C}{E C} = \frac{D F}{B D}$

查看试题解析
6. 顺次联结直角梯形各边中点所得到的四边形可能是（）

A、菱形； B、矩形； C、梯形； D、正方形．

查看试题解析

二、填空题

7. 已知f（x）=x³ -1，那么f（2）=

查看试题解析
8. 如果函数y＝kx（k≠0）的图象经过第二、四象限，那么y的值随x的值增大而．（填“增大”或“减小”）

查看试题解析
9. 在①平行四边形；②等腰三角形；③等腰梯形；④圆四个图形中，一定是轴对称图形的有（填序号）．

查看试题解析
10. 如图，△ABC在边长为1个单位的方格纸中，它的顶点在小正方形顶点位置，那么cotB的值为

查看试题解析
11. 正十边形的中心角等于度．

查看试题解析
12. 菱形的两条对角线长分别为5和12，那么这个菱形的面积为

查看试题解析
13. 如图，已知Rt△ABC中，∠BCA=90°，CD是斜边上的中线，BC=12，AC=5，那么CD=.

查看试题解析
14. 如图，线段AD与BC相交于点G， AB//CD， $\frac{A B}{C D} = \frac{1}{2}$ ，设 $\vec{G B} = \vec{a}$ ， $\vec{G A} = \vec{b}$ ，那么向量 $\vec{C D}$ 用向量 $\vec{a} ， \vec{b}$ 表示是

查看试题解析
15. 已知在等边△ABC中，AB=2，如果以点C为圆心的圆与边AB有且只有一个公共点，那么⊙C的半径是

查看试题解析
16. 已知两圆的半径长分别为2和5，两圆的圆心距为d，如果两圆没有公共点，那么d的取值范围是

查看试题解析
17. 如图， $▱ A B C D$ 中，E是边AD的中点，BE交对角线AC于点F，那么S△AFB ：S_四_边_形FEDC的值为

查看试题解析
18. 如图，已知在Rt△ABC中，∠C=90°，AC=BC=2，点D在边BC上，将△ABC沿直线AD翻折，使点C落在点 $C^{'}$ 处，联结 $A C^{'}$ ，直线 $A C^{'}$ 与边CB的延长线相交于点F，如果∠DAB=∠BAF，那么BF=

查看试题解析

三、解答题

19. 计算： $2 7^{\frac{1}{3}} + | 2 - \sqrt{3} | - (\sqrt{5} - \sqrt{2})^{0} + 2 c o s 30 °$

查看试题解析
20. 如图，在平面直角坐标系xOy中，反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图像与正比例函数y = 2x的图像的交点A在第一象限，点A的纵坐标比横坐标大1

(1)、求点A的坐标和反比例函数的解析式

(2)、点P在射线OA上，过点P作x轴的垂线交双曲线于点B．如果点B的纵坐标为1，求△PAB的面积

查看试题解析
21. 如图，已知⊙O的直径AB=10，点P是弦BC上一点，联结OP，∠OPB=45°，PC=1，求弦BC的长．

查看试题解析
22. 某山山脚到山顶有一条登山路，登山爱好者小李沿此路上山走到山顶，休息了一会儿后再原路返回．在下山途中，小李收到消息，需及时回到山脚，于是加速下山，小李下山过程中收到消息前所行的路程与收到消息后所行的路程之比为2：3，其间小李离开山脚的路程y（米）与离开山脚的时间x （分）（x>0）之间的函数关系如图9中折线OABCD所示．根据图像提供的信息，回答下列问题

(1)、这条登山路的全长为米；小李在山顶休息了分钟；

(2)、如果小李在下山途中没有收到消息，下山的速度一直保持不变，求小李实际提前了多少时间回到山脚．

查看试题解析
23. 已知：如图，在菱形ABCD中，对角线AC、BD交于点E，点M是CD中点，联结EM并延长，交∠DCB的外角∠DCN的平分线于点F．

(1)、求证： ME = MF；

(2)、联结DF，如果AB²= EB·BD，求证：四边形DECF是正方形．

查看试题解析
24. 在平面直角坐标系xOy中（如图），已知抛物线y=x² - bx+c经过A（-1.2）、B（0，-1）两点．

(1)、求抛物线的表达式及顶点P的坐标；

(2)、将抛物线y=x² - bx+c向左平移（ $\sqrt{3}$ +1）个单位，设平移后的抛物线顶点为点P'．
①求∠BP'P的度数；
②将线段P'B绕点B按逆时针方向旋转150°，点P’落在点M处，点N是平移后的抛物线上的一点，当△MNB的面积为1时，求点N的坐标．

查看试题解析
25. 在等腰梯形ABCD中，DC//AB，AB= 6， $t a n B = 2 \sqrt{2}$ ，过点A作AH⊥BC，垂足为点H．

(1)、当点C与点H重合时（如图），求线段BC的长；

(2)、当点C不与点H重合时，联结AC，作△ACH的外接圆O．
①当点C在BH的延长线上时（如图），设CH=x，CD = y，求y与x的函数解析式，并写出定义域；
②延长CD交圆O于点G，如果△ACH与△ACG全等，求CD的长

查看试题解析