上海市虹口区2021-2022学年九年级下学期期中数学试题

试卷更新日期：2022-04-29 类型：期中考试

进入出卷网下载

一、单选题

1. 下列实数中，有理数是（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{π}{3}$ C、 $\frac{1}{3}$ D、 $3^{\frac{1}{3}}$

查看试题解析
2. 在下列各组根式中，是同类二次根式的是（）

A、 $\sqrt{2}$ 和 $\sqrt{12}$ B、 $\sqrt{5}$ 和 $\sqrt{\frac{4}{5}}$ C、 $\sqrt{a b}$ 和 $\sqrt{a b^{4}}$ D、 $\sqrt{a^{2} - 1}$ 和 $\sqrt{a + 1}$

查看试题解析
3. 下列命题中，正确的是（）

A、正多边形都是中心对称图形 B、正多边形一个内角的大小与边数成正比例 C、正多边形一个外角的大小与边数成反比例 D、边数大于3的正多边形的对角线长都相等

查看试题解析
4. 将抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 向左平移两个单位，以下不改变的是（）

A、开口方向 B、对称轴 C、y随x的变化情况 D、与y轴的交点

查看试题解析
5. 六个学生进行投篮比赛，投进的个数分别为2、10、3、3、13、5，这六个数的中位数为（）

A、3 B、4 C、5 D、6

查看试题解析
6. 已知圆 $O_{1}$ 、圆 $O_{2}$ 的半径不相等，圆 $O_{1}$ 的半径长为5，若圆 $O_{2}$ 上的点A满足 $A O_{1} = 5$ ，则圆 $O_{1}$ 与圆 $O_{2}$ 的位置关系是（）

A、相交或相切 B、相切或相离 C、相交或内含 D、相切或内含

查看试题解析

二、填空题

7. 计算 $a^{6} \div a^{3} =$ .

查看试题解析
8. 已知 $f (x) = \frac{2}{x^{2} - 1}$ ，则 $f (- \sqrt{3}) =$ ．

查看试题解析
9. 不等式组 ${\begin{array}{l} x - 1 > 0 \\ 2 x + 3 > 0 \end{array}$ 的解集是．

查看试题解析
10. 方程 $\sqrt{2 - x} = 2$ 的解是．

查看试题解析
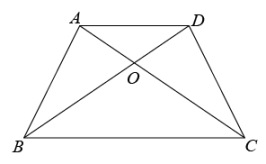
11. 如果关于x的一元二次方程 $x^{2} - 3 x + k = 0$ 有两个相等的实数根，那么实数k的值是.

查看试题解析
12. 已知点P位于第三象限内，且点P到两坐标轴的距离分别为3和2．若反比例函数图象经过点P，则该反比例函数的解析式为．

查看试题解析
13. 女生小琳所在班级共有40名学生，其中女生占60%.现学校组织部分女生去市三女中参观，需要从小琳所在班级的女生当中随机抽取一名女生参加，那么小琳被抽到的概率是．

查看试题解析
14. 已知平行四边形相邻两个内角相差40°，则该平行四边形中较小内角的度数是．

查看试题解析
15. 半径为4的圆的内接正三角形的边长为．

查看试题解析
16. 如图，已知梯形ABCD中， $A D ∥ B C$ ，对角线AC、BD交于点O， $\frac{S_{△ A O D}}{S_{△ B O C}} = \frac{1}{4}$ ．设 $\vec{A D} = \vec{a}$ ， $\vec{A B} = \vec{b}$ ，则 $\vec{A O} =$ ．（用含 $\vec{a}$ 、 $\vec{b}$ 的式子表示）

查看试题解析
17. 如图，在四边形ABCD中， $∠ A B C = ∠ A D C = 90 ° ， A C = 26 ， B D = 24$ ，M、N分别是AC、BD的中点，则线段MN的长为

查看试题解析
18. 已知 $l_{1} ∥ l_{2}$ ， $l_{1}$ 、 $l_{2}$ 之间的距离是5cm，圆心O到直线 $l_{1}$ 的距离是2cm，如果圆O与直线 $l_{1}$ 、 $l_{2}$ 有三个公共点，那么圆O的半径为cm．

查看试题解析

三、解答题

19. 计算： $| \sqrt{3} - 2 | - 3 6^{\frac{1}{2}} + \sqrt{\frac{4}{3}} + {(\frac{1}{2})}^{- 2}$

查看试题解析
20. 解方程组： ${\begin{array}{l} x - y = 10 ① \\ x^{2} - 5 x y - 6 y^{2} = 0 ② \end{array}$

查看试题解析
21. 如图，AH是△ABC的高，D是边AB上一点，CD与AH交于点E．已知 $A B = A C$ ， $A D ： D B = 3 ： 5$ ．

(1)、求 $D E ： E C$ ；

(2)、若以H为圆心、HB为半径的圆恰好经过点D，求 $c o s B$ 的值．

查看试题解析
22. 已知反比例函数 $y = \frac{12}{x}$ 的图像和一次函数 $y = k x - 7$ 的图像都经过点 $P (m ， 2)$ ．

(1)、求这个一次函数的解析式；

(2)、如果等腰梯形ABCD的顶点A、B在这个一次函数的图象上，顶点C、D在这个反比例函数的图象上，两底AD、BC与y轴平行，且A和B的横坐标分别为a和 $a + 2$ ，求a的值．

查看试题解析
23. 已知：如图，梯形ABCD中，AD∥BC，DE∥AB， $D E$ 与对角线 $A C$ 交于点 $F$ ， $F G$ ∥ $A D$ ，且FG=EF.

(1)、求证：四边形 $A B E D$ 是菱形；

(2)、联结AE，又知AC⊥ED，求证： $\frac{1}{2} A E^{2} = E F · E D$ .

查看试题解析
24. 如图，抛物线y=ax²+6x+c交x轴于A，B两点，交y轴于点C．直线y=x﹣5经过点B，C．

(1)、求抛物线的解析式；

(2)、过点A的直线交直线BC于点M．
①当AM⊥BC时，过抛物线上一动点P（不与点B，C重合），作直线AM的平行线交直线BC于点Q，若以点A，M，P，Q为顶点的四边形是平行四边形，求点P的横坐标；
②连接AC，当直线AM与直线BC的夹角等于∠ACB的2倍时，请直接写出点M的坐标．

查看试题解析
25. 如图，△ABC中， $A B = A C$ ， $B D$ 是AC边上的中线，AO平分 $∠ B A C$ 且交BD于点O．

(1)、求证： $B O = 2 O D$ ；

(2)、当△BCD是等腰三角形时，求 $∠ C B D$ 的余弦值；

(3)、以O为圆心、OD长为半径的圆交线段BO于点E，连结CE．当△CDE与△AOB相似时，求AB：BC的值．

查看试题解析